Ae 11 approche des lois de newton avec correction

Terminale S
AE 11_Approche des lois de Newton
M.Meyniel 1/8
LES LOIS DE NEWTON AUX JEUX OLYMPIQUES
Objectifs : - Vérifier et appréhender vectoriellement la première loi de Newton.
- Approcher la deuxième loi de Newton.
Document 1 : Le principe d’inertie (Newton, 1666)
" Tout système isolé ou pseudo-isolé persévère dans son état de repos ou de mouvement rectiligne uniforme."
Rq : * Un système isolé n’est soumis à aucune force.
Un système pseudo-isolé est soumis à des forces dont la résultante (= la somme) est nulle.
Document 2 : Quelques sports olympiques
Le curling
Le curling trouverait ses origines vers le XVIème siècle en Ecosse, notamment en raison des conditions
climatiques hivernales favorisant la formation d'une couche de glace permettant la pratique de ce sport. Maintenant
répandu à travers le monde, ce sport est olympique depuis les Jeux Olympiques d'hiver de 1998 à Nagano au Japon.
Le but est de lancer une "pierre" à travers une patinoire pour l'amener le plus près possible du centre d’une cible. Le
mouvement de la pierre peut être considéré sans frottement sur une durée relativement courte.
L'enregistrement n°1 donné en annexe donne les positions d’une pierre à intervalles de temps régulier.
La luge
La luge est un sport olympique de vitesse, consistant à descendre une piste verglacée sans frein et en un
minimum de temps. Elle se pratique en position allongée sur le dos, seul ou à deux personnes. Les spécialistes
peuvent atteindre des vitesses proches des 120 km.h-1.
Lors d'une descente, un lugeur lancé à pleine vitesse, dans sa deuxième moitié de descente, a une vitesse constante
comprise entre 110 et 120 km.h-1. Attaquant un virage dont le rayon de courbure vaut environ 25 m, ce lugeur est
soumis à une accélération très importante. Les efforts que ce lugeur doit fournir pour maintenir son corps droit et
gainé sur la luge sont alors considérables.
L'enregistrement n°2 de l'annexe donne différentes positions du lugeur dans un virage de la piste de luge.
Le basket
Le basket-ball ou basketball, fréquemment désigné en français par son apocope basket, est un sport collectif
opposant deux équipes de cinq joueurs sur un terrain rectangulaire. L'objectif de chaque équipe est de faire passer
un ballon au sein d'un arceau de 46 cm de diamètre, fixé à un panneau et placé à 3,05 m du sol : le panier.
L’équipe de France féminine est vice-championne olympique depuis les JO de Londres de 2012. L’équipe masculine
avait aussi réussi à décrocher une médaille d’argent aux JO de Sydney en 2000, battus eux-aussi par les USA.
La vidéo « TPSecondeProjectile.avi » (fichier à ouvrir sous LatisPro®) permet d’étudier le mouvement d’un ballon de
basket.
Le saut à ski
Le saut à ski, discipline olympique également, a pour but de parcourir le maximum de distance dans les airs.
Afin d’acquérir le maximum de vitesse, le sauteur se laisse glisser sur un tremplin constitué de deux parties :
- une partie plane et fortement inclinée permettant de gagner en vitesse.
- une partie incurvée permettant au sauteur de prendre idéalement son envol.
En repérant par rapport à la piste inclinée et à intervalle de temps réguliers, la position du centre de gravité du
sauteur lors de sa prise d'élan (départ arrêté), on obtient alors l'enregistrement n°3 donné en annexe.

Terminale S
AE 11_Approche des lois de Newton
M.Meyniel 2/8
Document 3 : Le vecteur-vitesse 
Soient G(t) la position du centre d’inertie G d’un système
à l’instant t et G(t+ t) celle à l'instant t+ t
* Le vecteur-vitesse moyenne  du système entre ces deux
positions par : 
* Si l’on souhaite approchée le vecteur-vitesse instantanée  , c’est-à-dire à un moment donné, l’intervalle de
temps t doit être le plus petit possible et tendre vers « 0 » :
Le vecteur-vitesse instantanée  correspond donc à la dérivée du vecteur-position  par rapport au temps.
Dans la pratique, pour approcher la valeur de ce vecteur-vitesse instantanée au
temps t, on considère les points juste avant et juste après pour calculer la valeur
du vecteur-vitesse moyenne sur le plus petit intervalle de temps possible :
Document 4 : Le vecteur-accélération 
Comme pour le vecteur-vitesse on peut définir un vecteur-accélération  du centre d’inertie G du système :
* Le vecteur-accélération moyenne  se définit par : 
* Le vecteur-accélération instantanée 
 se définit par : 
 avec a en m.s-2
Dans la pratique, pour tracer le vecteur-accélération instantanée,
on procède comme pour la vitesse sur un intervalle de temps minimal : 
I. « Le mouvement de la pierre de curling vérifie-t-il le principe d’inertie ? »
1 – Dans quel référentiel est étudié le mouvement de la pierre de curling ?
2 – Faire le bilan des forces s’exerçant sur le système et exprimer la résultante des forces «  ».
3 – a. Comment évolue la vitesse du mobile au cours du temps ?
b. Calculer la valeur du vecteur-vitesse  puis tracer le vecteur-vitesse  au point G3 en
précisant l’échelle choisie.
c. Sans faire de calcul, tracer les vecteurs-vitesse  &  aux points G6 & G8.
4 – Que peut-on dire du vecteur-variation de vitesse  et donc du vecteur-accélération  ?
5 – Qualifier la nature du mouvement suivi par la pierre de curling. Attention : il y a toujours deux
caractéristiques à préciser pour déterminer la nature d’un mouvement.
6 – Préciser si la première loi de Newton est vérifiée et proposer un énoncé vectoriel de cette loi.
O
G(t)
G(t+t)
sens du
mouvement
trajectoire
de l'objet

Terminale S
AE 11_Approche des lois de Newton
M.Meyniel 3/8
II. Vers la deuxième loi de Newton …
1. Etude du mouvement du lugeur.
1. Etablir le bilan des forces s’exerçant sur le système après avoir précisé le référentiel d’étude.
2. Tracer les vecteurs-vitesse  &  aux points G5 & G7.
3. Construire alors le vecteur-variation de vitesse  au point G6.
4. Tracer le vecteur-accélération  au point G6 en précisant l’échelle choisie.
5. Exploitation des résultats :
a. Comment évolue la vitesse du mobile au cours du temps ?
b. En déduire la nature du mouvement.
c. Comparer la direction et le sens du vecteur-accélération  avec ceux de la résultante des
forces  .
2. Etude du mouvement d’un ballon de basket.
 On s’intéresse au mouvement d’un ballon de basket. A l’aide du logiciel LatisPro®, en vous servant de l’outil
de pointage, repérer la trajectoire du ballon y(x).
 Cliquer sur « Transférer vers les vecteurs » pour obtenir la trajectoire ainsi que le vecteur-vitesse  et le
vecteur-accélération  en déplaçant la souris sur les différentes positions obtenues.
1. Recopier l’allure de la trajectoire y(x) et représenter les vecteurs  et  en quelques points.
Attention : on donnera une direction « moyenne » pour le vecteur-accélération.
2. Exploitation des résultats :
a. Indiquer la direction du vecteur-vitesse  par rapport à la trajectoire.
b. L’expression vectorielle de la deuxième loi de Newton est 
Justifier que la direction et le sens du vecteur-accélération  sont en accord avec la seconde loi
de Newton. Donner la valeur théorique de l’accélération et la comparer à celle trouvée par la
simulation vidéo.
3. Etude du mouvement du skieur.
1. Etablir le bilan des forces s’exerçant sur le système après avoir précisé le référentiel d’étude.
2. Tracer les vecteurs-vitesse aux points G4 , G6 , G8 et G10.
3. Construire alors les vecteurs-variation de vitesse  et  au point G5 et G9.
4. Tracer les vecteurs-accélération  et  au point G5 et G9 en précisant l’échelle choisie.
5. Exploitation des résultats :
a. Comment évolue la vitesse du mobile au cours du temps ?
b. En déduire la nature du mouvement.
c. Comparer la direction et le sens du vecteur-accélération  avec ceux de la résultante des
forces  .
Pour le plaisir … : « Du sauteur à ski et du lugeur, lequel est soumis à l’accélération la plus forte ? »
« Quelle différence majeure voyez-vous entre ces deux types d’accélération ? Les qualifier. »
avec m est la masse de
l’objet en mouvement.

Terminale S
AE 11_Approche des lois de Newton
M.Meyniel 4/8
ANNEXE
Enregistrement n°1 : 1 cm correspond à 10 cm sur la piste de curling.
Intervalle de temps entre deux positions consécutives : t = 100 ms
G0 G1 G2 G3 G4 G5 G6 G7 G8 G9 G10 G11
Sens du
mouvement
Enregistrement n°2 : 1 cm correspond à 4 m sur la piste de luge.
Intervalle de temps entre deux positions consécutives : t = 270 ms
G0
G3
G2
G1
G5
G4
G8
G7
G6
G9
G10
G11
Enregistrement n°3 : 1 cm correspond à 1 m sur la piste d'élan de saut à ski.
Intervalle de temps entre deux positions consécutives : t = 200 ms
G0G1G2 G3 G4 G5 G6 G7 G8 G9 G10 G11
Sens du
mouvement

Terminale S
AE 11_Approche des lois de Newton
M.Meyniel 5/8
CORRECTION : LES LOIS DE NEWTON AUX JEUX OLYMPIQUES
Objectifs : - Vérifier la première loi de Newton et voir sa définition vectorielle.
- Découvrir la deuxième loi de Newton.
I. « Le mouvement de la pierre de curling vérifie-t-il le principe d’inertie ? »
Système {pierre de curling}
1 – Le mouvement du curling est étudié dans un référentiel terrestre supposé galiléen, la glace par exemple.
2 – Bilan des forces :
- poids de la pierre  (point d’application : centre de gravité ;
direction : verticale ; sens : vers le centre de la Terre) ;
- la réaction du sol  (point d’application : centre de la surface de contact ;
direction : verticale ; sens : du sol vers le solide) ;
 Les forces agissent verticalement. Or, le mobile n’a aucun mouvement vertical donc les forces qui
s’exercent sur le système se compensent : 
=> Les forces se compensent donc.
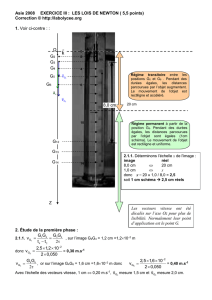
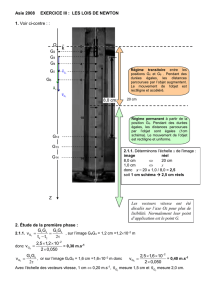
On choisi une échelle de représentation des vecteurs vitesses 1 cm  1 m.s-1. On représente les vecteurs vitesses par
des segments fléchés de 1,5 cm.
3 – a. Les points sont équidistants et alignés donc la vitesse est constante en direction, sens et valeur.
b. v3 = 
 =   =   = 1,50 m.s-1
Représentation des vecteurs : On utilise la proportionnalité avec l’échelle { 1 cm  100 cm.s-1 }
Le vecteur-vitesse est représenté par une flèche de 1,5 cm.
c. Les vecteurs-vitesse  &  ont même direction, même sens et même intensité que  car la
vitesse ne varie pas.
4 – Le vecteur-variation de vitesse  est donc nul tout comme le vecteur-accélération  puisque le vecteur-
vitesse ne varie pas.
5 – La vitesse est constante, la trajectoire est une droite donc le mouvement est uniforme et rectiligne.
6 – Le mouvement est uniforme rectiligne et la somme des forces est nulle donc la première loi de Newton est
vérifiée.
Dans un référentiel galiléen : 
Enregistrement n°1 : 1 cm correspond à 10 cm sur la piste de curling.
Intervalle de temps entre deux positions consécutives : t = 100 ms
G0 G1 G2 G3 G4 G5 G6 G7 G8 G9 G10 G11
Sens du
mouvement
ATTENTION A L’ECHELLE :
Schéma Réel
1,0 cm ↔ 10 cm
3,0 cm ↔ G2G4 = 3,0  10 / 1,0 = 30 cm