Bac blanc - Web Sciences

Page 1
Terminales S Bac blanc de sciences physiques
(3 pages)
Exercice n°1 (7 points) Pile
On souhaite réaliser une pile au laboratoire. Pour cela, on dispose d'une lame de zinc et d'une lame
de cuivre ainsi que d'un volume V1=100mL, d'une solution aqueuse de sulfate de zinc de
concentration molaire en soluté apporté C1=1,0mol.L-1 et d'un volume V2=100mL d'une solution
aqueuse de sulfate de cuivre de concentration molaire en soluté apporté C2=1,0mol.L-1. On dispose
de plus d’un pont salin.
L'expérience est réalisée à la température de 25°C. A cette température, la constante d'équilibre
associée à l'équation:
Cu2+(aq) + Zn(s) = Zn2+(aq) + Cu(s)
est K=4,6x1036.
La pile ainsi réalisée est placée dans un circuit électrique comportant une résistance et un
interrupteur. On ferme ce circuit électrique à l'instant de date t0=0s.
1. Faire un schéma légendé de cette pile. Compléter le schéma avec la résistance et l'interrupteur.
2. Déterminer le quotient de réaction Qr,i du système ainsi constitué à l'instant de date t0. En déduire
le sens d'évolution spontanée du système.
3. Pour chaque électrode, écrire la demi-équation correspondant au couple qui intervient.
4. En déduire, en justifiant la réponse, à quel métal correspond le pôle + de la pile et à quel métal
correspond le pôle -.
5. D'après la théorie, on considère que la pile s'arrête de fonctionner quand le réactif limitant,
constitué soit par les ions Cu2+(aq) soit par les ions Zn2+(aq), a été complètement consommé.
En utilisant l'équation de la réaction se produisant à l'une des électrodes, calculer la quantité
maximale d'électricité que pourrait théoriquement débiter cette pile.
6. Combien de temps la pile peut-elle fonctionner si elle débite un courant constant d’intensité
I=15mA ?
7. Quelle est la masse de métal consommée ?
Données : Constante d'Avogadro : NA=6,02.1023mol-1.
Charge électrique élémentaire : e=1,6.10-19C.
Masse molaire atomique du cuivre : M(Cu)=63,5g.mol-1.
Masse molaire atomique du zinc : M(Zn)=65,4g.mol-1.
Exercice n°2 (6 points) Energie du Soleil
Une grande partie de l’énergie émise par le Soleil est attribuée à un ensemble de réactions nucléaires
dont le bilan peut s’écrire :
e2HeH40
1
4
2
1
1+→
1. Quelle est l’origine de l’énergie émise par le Soleil ? Quel type de réaction est ici mis en jeu ?
2. Calculer E1 l’énergie de masse des réactifs, puis E2 l’énergie de masse des produits de la réaction.
3. En déduire l’énergie E libérée par cette réaction ? Evaluer la fraction 1
E
E
=α. Montrer que cette
fraction α peut aussi s’écrire 1
m4m∆ et représente la fraction de la masse du Soleil convertie en
énergie libérée.
4. La masse actuelle du Soleil est estimée à MS=2,0.1030kg. Si l’on admet que seule la réaction ci-
dessus intervient et qu’une proportion de 10% de la masse totale est placée dans les conditions où

Page 2
la réaction peut se produire, évaluer la masse M que le Soleil peut perdre encore dans ces
conditions pour rayonner l’énergie correspondante dans les siècles futurs.
5. La puissance totale rayonnée par le Soleil est P=3,7.1026W.
a. Calculer en kg.s-1 la masse perdue par seconde par le Soleil.
b. En utilisant le résultat de la question 4, on peut évaluer approximativement l’espérance de vie
du Soleil. Calculer cette espérance de vie T en seconde puis en année (à titre indicatif, l’âge
actuellement admis pour le Soleil est 5.109ans).
Données :
1u=1,66.10-27kg ; 1eV=1,60.10-19J ; c=3,00.108m.s-1 ; énergie de masse associée à l’unité de masse
atomique : 931,5MeV ; masse de l’électron ou du positon : m3=5,4858.10-4u ; masse du noyau
d’hydrogène : m1=1,007284u ; masse du noyau d’hélium : m2=4,001502u.
Exercice n°3 (7 points) Détermination expérimentale de l’inductance d’une bobine
La bobine considérée est résistive (de résistance r) et inductive (d'inductance L).
I. À l'aide d'un générateur de tension continue, on alimente la bobine puis on insère des multimètres
dans le circuit afin de mesurer l'intensité du courant qui la traverse et la tension aux bornes du
générateur.
La résistance r de la bobine a été trouvée égale à 10Ω. Expliquer brièvement comment on a pu
déterminer expérimentalement cette valeur à partir du
montage proposé.
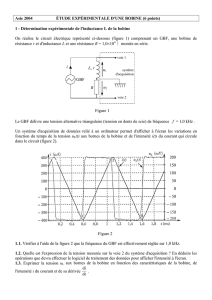
II. Un générateur basse fréquence délivrant une tension en
créneaux (0V pendant une demi-période et 4V pendant
l'autre demi-période; f=200Hz) alimente la bobine (r, L)
associée en série avec un conducteur ohmique de
résistance R’=420Ω (figure 1). Un dispositif d'acquisition
de données relié à un ordinateur permet de suivre
l'évolution en fonction du temps de l'intensité i du courant
qui traverse la bobine. L'enregistrement réalisé (figure 2)
correspond à la demi-période pendant laquelle la tension
aux bornes du générateur est 4 V.
1. Quel élément du circuit est responsable du retard à l'établissement du courant?
2. Mesurer la constante de temps τ du circuit en utilisant la figure 2.
Rappel: La constante de temps τ est la durée au bout de laquelle l'intensité du courant atteint
63 % de sa valeur maximale.
3. En déduire la valeur de L sachant que 'RrL
+
=τ.
III. Un condensateur de capacité C=0,25µF est chargé
à l'aide d'un générateur de tension de force

Page 3
électromotrice E=6,0V puis déconnecté du générateur.
À la date t=0, le condensateur chargé est relié à la bobine considérée précédemment (figure 3).
L’évolution de la tension uC au cours du temps est enregistrée à l'aide de l'ordinateur (figure 4).
1. Comment appelle-t-on le type d'oscillations observées à la figure 4?
2. Comment interpréter la décroissance des oscillations?
3. Établir l'équation différentielle à laquelle satisfait la tension uC en respectant l'orientation
d'intensité qui est indiquée sur la figure 3.
4. Mesurer la pseudopériode T’ des oscillations.
5. On considère que la résistance de la bobine est nulle:
a. Écrire la nouvelle expression de l'équation différentielle à laquelle satisfait uC.
b. Quelle est l'expression littérale de la période des oscillations qui prennent naissance dans le
circuit (dans le cas où la résistance r de la bobine est nulle)?
6. Calculer la valeur de l'inductance de la bobine en admettant que la pseudopériode est identique
à la période.