Devoir surveillé de sciences physiques n°6

Nom : ………….. Prénom :…..………………
Durée : 1 heure
L’usage des calculatrices est autorisé.
0,5 pt sur l’ensemble des 2 exercices pour les chiffres significatifs.
Exercice 1 (7,5 pts) :
2.
1. On place l'interrupteur en position haute. Quelle est en régime permanent l'intensité Io du courant
dans le circuit.
2. A l'instant t = 0 s , on bascule l'interrupteur en position basse. Etablir l'équation différentielle à laquelle
obéit l'intensité i du courant dans le circuit.
Vérifier que l’expression i = Io e
t
est bien la solution de cette équation différentielle. Rappeler au préalable
l'expression de .
3. Soit U
BC
la tension aux bornes du conducteur ohmique R. Soit t
1 le temps au bout duquel
U
BC
atteint 90 % de sa
valeur maximale et t
2 le temps au bout duquel
U
BC
atteint l 0 % de sa valeur maximale.
Exprimer td = t
2 -
t
1 en fonction de
.
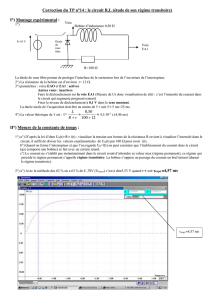
A partir de la courbe U
BC
= f(t) représentée ci-dessous déterminer td, et en déduire la valeur de . Vérifier cette
valeur en faisant l'application numérique à partir de l'expression de .
- Devoir surveillé de sciences physiques n°6 -
Physique (20 pts)

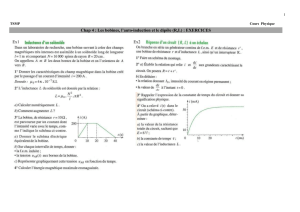
Exercice 2 (12 pts) :
On branche en série une pile de force électromotrice E et de résistance r, un interrupteur K, une bobine d'inductance
L et de résistance R1, et un conducteur ohmique de résistance R2 = 50  (figure 1).
Un ordinateur relié au montage par une interface appropriée, permet d'enregistrer au cours du temps les valeurs des
tensions.
1. A l'instant t = 0 s, on ferme l'interrupteur K, et on procède à l'enregistrement. On obtient les courbes Y1 = f(t) et
Y2 = g(t) (figure 2).
a) Quelles sont les grandeurs électriques observées sur les voies A et B ?
Identifier alors Y1 et Y2. Justifier la réponse.
b) A partir de la courbe représentant la variation de i (voie Y2 ) intensité du courant dans le circuit, expliquer le
comportement électrique de la bobine.
c) Donner la valeur de la force électromotrice E de la pile.
2. Lorsque le régime permanent est établi, l'intensité i prend la valeur Ip, tandis que Y2 prend la valeur Yp .
a) Donner les expressions littérales des tensions UAM, UAB et UBM·
b) Montrer, en utilisant les courbes (figure 2), que la bobine a une résistance R1 non nulle.
c) Calculer:
- l'intensité Ip ;
- la résistance interne r de la pile;
-la résistance R1 de la bobine.
3. Le circuit étudié peut être caractérisé par une constante de temps  , qui permet d'évaluer la durée nécessaire à
l'établissement d'un régime permanent dans ce circuit. Pour un circuit (RL), on pose :  =
R
L
.
a) Donner la valeur de déterminée graphiquement.
b) En déduire la valeur de l'inductance L de la bobine, et calculer l'énergie emmagasinée par celle-ci quand le
régime permanent est établi.