Rapport_de_recherche_p1

Université Sidi Mohamed Ben Abdellah
Faculté des Science et Techniques
Fès
Rapport de recherche
Encadré par :
Pr : A.MAJDA
TADMSIR15

1
SOMMAIRE :
Introduction ...................................................................................................................................................................... 2
Inférence dans les réseaux bayésiens .............................................................................................................................. 2
Définition de l’inférence ................................................................................................................................................ 2
Inférence dans les réseaux bayésiens ............................................................................................................................ 2
Théorème de bayes ........................................................................................................................................................ 2
Apprentissage des réseaux bayésiens .............................................................................................................................. 4
Apprentissage des paramètres ...................................................................................................................................... 4
Apprentissage de la structure ........................................................................................................................................ 5
Le classifieur bayésien naïf ............................................................................................................................................... 5
Définition de La classification naïve bayésienne ........................................................................................................... 5
Avantages et inconvénients ........................................................................................................................................... 6
Conclusion ......................................................................................................................................................................... 6
Références ......................................................................................................................................................................... 7

2
Introduction :
Les réseaux bayésiens sont des outils puissants pour le raisonnement et la décision sous incertitude. Une
forme très simplifiée de ces réseaux est appelée réseaux bayésiens naïfs, qui disposent d’un mécanisme
d’inférence particulièrement efficace. Et parmi les simplifications de ces réseaux l’utilisation de classificateur
bayésien naïf.
Inférence dans les réseaux bayésiens:
Définition de l'inférence:
L’inférence est l’acte où le processus de tirer des conclusions logiques de locaux connus où supposés être
vraie.
Inférence dans les réseaux bayésiens:
L'inférence dans un réseau bayésien est le calcul des probabilités a posteriori dans le réseau, étant donné
des nouvelles informations observées. Il s'agit d'un problème de calcul car, grâce aux opérations sur les
probabilités et au théorème de Bayes, toutes les probabilités a posteriori possibles dans un réseau peuvent
être calculées. Ainsi, étant donné un ensemble d'évidences (de variables instanciées) Y, le problème de
l'inférence dans G=(V, E) est de calculer P(X | Y) avec X est inclus dans V, et Y est inclus dans V. Si Y est vide
(aucune évidence), cela revient à calculer P(X). Intuitivement, il s'agit de répondre à une question de
probabilité sur le réseau.
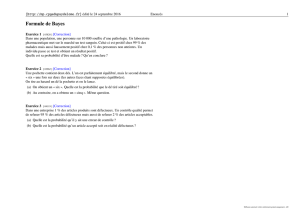
Théorème de Bayes :
C’est un résultat de base en théorie des probabilités, issu des travaux du révérend
Thomas Bayes (1702-1761), présenté à titre posthume en 1763. Voici ces résultats :
P(A) : désigne la probabilité à priori de A
P(A|B) : désigne la probabilité a posteriori de A sachant B (ou encore de A sous condition B)
P(A∩ 𝐵) : désigne la probabilité que A et B aient tous les deux lieu.
Le théorème de Bayes permet d'inverser les probabilités. C'est-à-dire que si l'on connaît les conséquences
d'une cause, l'observation des effets permet de remonter aux causes, c'est l'effet d'induction « bottom-up ».
Sachant aussi qu'une lecture littéral du théorème de Bayes permet une induction « top-down », c'est à dire à
partir des causes en déduire les conséquences.
Deux grandes catégories d'algorithmes d'inférence viennent naturellement :
 Algorithmes exacts
 Bucket Elimination
 Message Passing (Pearl 88) pour les arbres
 Junction tree(Jensen 90)
 Algorithmes approchés
 Echantillonnage :Markov Chain Monte Carlo
 Méthodes variationnelles

3
Message Passing
 Chaque nœud envoie des messages à ses voisins
 L’algorithme ne marche que dans le cas des arbres (généralisé au cas des poly-arbres)
Junction Tree
 Message Passing ne s’applique bien qu’aux arbres
 Besoin d’un algorithme plus général
 Principe :
 Transformer le graphe en un arbre (non orienté)...
 Arbre = arbre de jonction des cliques maximales du graphe moralisé et triangulé
Moralisation = marier les parents et "désorienter" le graphe
Triangulation = éviter les cycles dans le graphe non orienté.
 Moralisation : marier les parents de chaque nœud
 Triangulation : tout cycle de longueur au moins 4 doit contenir une corde (arête reliant deux sommets
non consécutifs sur le cycle).
 aucun sous-graphe cyclique de longueur > 3
 Triangulation optimale pour des graphes non-dirigés = NP-difficile
 Clique = sous-graphe du RB dont les nœuds sont complétement connectés
 Clique maximale = l’ajout d’un autre nœud à cette clique ne donne pas une clique.
Théorème :
Si le graphe est moralisé et triangulé, alors les cliques peuvent être organisées en un arbre de jonction.

4
L’inférence se fait au niveau de
Apprentissage des réseaux bayésiens
Un réseau bayésien est constitué à la fois d’un graphe (aspect qualitatif) et d’un ensemble de probabilités
conditionnelles (aspect quantitatif). L’apprentissage d’un réseau bayésien doit donc répondre aux deux
questions suivantes :
• Comment estimer les lois de probabilités conditionnelles ?
• Comment trouver la structure du réseau bayésien ?
Nous allons donc séparer le problème de l’apprentissage en deux parties :
 L’apprentissage des paramètres : où nous supposerons que la structure du réseau a été
fixée, et où il faudra estimer les probabilités conditionnelles de chaque nœud du réseau.
 L’apprentissage de la structure : où le but est de trouver le meilleur graphe représentant la
tâche à résoudre.
Apprentissage des paramètres
 À partir de données complètes :
Nous cherchons ici à estimer les distributions de probabilités (ou les paramètres des lois correspondantes) à partir de
données disponibles! Nous décrirons ici les méthodes les plus utilisées dans le cadre des réseaux bayésiens, selon que
les données à notre disposition sont complètes ou non.
Dans le cas où toutes les variables sont observées, la méthode la plus simple et la plus utilisée est l'estimation
statistique qui consiste à estimer la probabilité d'un événement par la fréquence d'apparition de l'événement dans la
base de données. Cette approche, appelée maximum de vraisemblance (MV), nous donne alors :
Dans la formule précédente Ni,j,k est le nombre d'événements dans la base de données pour lesquels la variable Xi est dans l'état xk
et ses parents sont dans la configuration cj.
 À partir de données incomplètes :
Dans les applications pratiques, les bases de données sont très souvent incomplètes. Certaines variables ne sont observées que
partiellement ou même jamais. La méthode d'estimation de paramètres avec des données incomplètes la plus couramment utilisée
est fondée sur l'algorithme itératif EM (Expectation Maximisation) proposé par Dempster.
Soit :
: N l'ensemble des données observées (visibles).