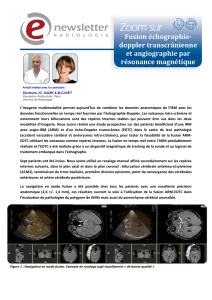
Fusion d`images en multimodalité.

Ch. Jégou, A. Bonmartin
Médecine Nucléaire - Imagerie fonctionnelle et métabolique - 2004 - vol.28 - n°11 553
Correspondance : Alain Bonmartin
Laboratoire de Biophysique - EA 3738 - Faculté de Médecine Lyon-Sud
BP 12 - 69921 Oullins cedex
Tél : [phone] - E-mail : [email protected]
Fusion d’images en multimodalité.
Ch. Jégou, A. Bonmartin EA 3738 - Faculté de Médecine Lyon-Sud - UCB Lyon 1
Centre TEP clinique - HCL - Centre Hospitalier Lyon-Sud
Résumé
La fusion d’images en multimodalité est la mise en correspondance spatiale d’images
acquises par des techniques différentes. Elle comporte deux étapes fondamentales : le recalage et
la visualisation. Le recalage est la recherche de la transformation géométrique qui aligne les
données. Son utilisation clinique suppose une validation préalable en utilisant des données de
référence. La description du processus de recalage se base sur le cadre défini pour la construc-
tion de la bibliothèque de fonctions Insight Toolkit (ITK). Les applications médicales principales
et quelques possibles évolutions de la fusion sont exposées.
Fusion / Recalage / Multimodalité
INTRODUCTION
!Aucune technique d’imagerie prise
isolément n’est, à l’heure actuelle, ni
suffisamment sensible, ni suffisam-
ment spécifique pour apporter à elle
seule l’information diagnostique sou-
haitée par le clinicien. L’apport de la
multimodalité en imagerie permet
d’améliorer cette information. Les ter-
mes de fusion multimodalité ou
intermodalité désignent l’alignement,
dans l’espace, de plusieurs images
issues de techniques d’imagerie dif-
férentes, et, dans ce domaine, la fu-
sion informatique est plus perfor-
mante que la fusion mentale effec-
tuée à partir de documents disjoints.
Ces associations ont donc pour but
de compléter les lacunes propres à
chaque modalité. Le plus souvent, on
souhaite superposer une image fonc-
tionnelle (scintigraphie, Tomographie
par Emission de Positons (TEP), To-
mographie par Emission Mono-
photonique (TEMP), Imagerie par Ré-
sonance Magnétique Fonctionnelle
(IRMf) avec une image anatomique
(radiographie, scanner à rayons X
(TDM), IRM, échographie) permettant
de situer plus précisément les fixa-

Fusion d'images en multimodalité
554 Médecine Nucléaire - Imagerie fonctionnelle et métabolique - 2004 - vol.28 - n°11
tions moléculaires. Dans la pratique
clinique, on fusionne des images pro-
venant d’un même patient (fusion
intra-sujet), et nous nous limiterons
à ce cadre. Cependant, la fusion inter-
sujets à aussi des applications : cons-
titution de modèles, d’atlas (atlas de
Talairach pour le cerveau par exem-
ple) pour des comparaisons anatomi-
ques ou fonctionnelles [1]. On peut
également fusionner des images is-
sues d’une même technique d’ima-
gerie. Dans ce cas on parlera de fu-
sion mono ou intra-modalité, utile
dans le suivi évolutif d’une patholo-
gie ou pour la constitution d’atlas.
On décrira successivement les diffé-
rentes étapes qui constituent la fu-
sion: le recalage, qui calcule la trans-
formation à appliquer pour mettre en
correspondance le jeu d’images, sa
validation, puis la visualisation et l’in-
teraction avec les images recalées.
Enfin, seront abordés les champs d’ap-
plication de la fusion et ses perspec-
tives.
LE RECALAGE
!On définit d’abord l’image fixe, ré-
férence sur laquelle on va aligner
l’image mobile en lui faisant subir
des transformations géométriques. Le
processus de recalage des images
peut ensuite se diviser en quatre éta-
pes, représentées dans la Figure 1Figure 1
Figure 1Figure 1
Figure 1,
selon la cadre mis en place pour la
constitution de la bibliothèque de
fonctions pour le recalage de l’Insight
Toolkit (ITK) [2].
Image Fixe
Image Mobile
Mesure
Interpolation
Transf
o
pixels
qualité de l'al
ig
pixels points
pixels
Figure 1 - Etapes du recalage
L’interpolation
!Après l’application d’une transfor-
mation, les centres des voxels (vo-
lume éléments) de l’image mobile ne
sont pas forcément alignés sur les
centres des voxels de l’image fixe.
L’interpolation consiste alors à éva-
luer les valeurs d’intensité de l’image
mobile pour les coordonnées en cor-
respondance avec les centres des
voxels de l’image fixe.
Parmi les techniques utilisées [3], la
plus fréquente est l’interpolation li-
néaire où l’intensité d’un point est
calculée par la combinaison des in-
tensités de ses voisins, affectées de
poids dépendant linéairement de la
distance au point considéré.
La transformation
!Les transformations sont classées en
deux grandes catégories selon leurs
degrés de liberté.
Les transformations linéairesLes transformations linéaires
Les transformations linéairesLes transformations linéaires
Les transformations linéaires
!Parmi les transformations linéaires,
on parle de transformation rigide lors-
que seules des translations et des ro-
tations sont autorisées. Une transfor-
mation affine est une transformation
rigide à laquelle s’ajoutent des fac-
teurs d’échelle et des torsions. Elle
permet de prendre en compte une
grande partie des distorsions spatia-
les usuelles.
Les transformations élastiquesLes transformations élastiques
Les transformations élastiquesLes transformations élastiques
Les transformations élastiques
Les transformations élastiques sont
plus déformantes que les transforma-
tions linéaires. Elles peuvent s’appli-
quer sur l’ensemble du volume, ou
être uniquement des déformations
locales, mieux adaptées à des varia-
tions complexes : correction des dé-
formations liées à l’acquisition,
recalage sur des structures en mou-
vement (cœur, poumon). La déforma-
tion peut être libre ou guidée par une
modélisation physique de l’élasticité
des tissus.
La mesure de l’alignement
ou mesure de similarité
!Le choix de la technique d’évalua-
tion de la qualité de l’alignement dé-
pend des images que l’on traite. Parmi
les techniques employées [4], on en
distingue deux grandes catégories :
celles qui utilisent des points de re-
père, et celles qui exploitent l’image
dans sa totalité.
Mesure de l’alignement utilisantMesure de l’alignement utilisant
Mesure de l’alignement utilisantMesure de l’alignement utilisant
Mesure de l’alignement utilisant
des points de repèredes points de repère
des points de repèredes points de repère
des points de repère
Le problème de la minimisation de
la distance entre les repères est ap-
pelé problème de Procruste. Pour les
transformations rigides, la solution
peut être calculée directement [5, 6].
Dans les autres cas, on peut par exem-
ple utiliser une minimisation itérative

Ch. Jégou, A. Bonmartin
Médecine Nucléaire - Imagerie fonctionnelle et métabolique - 2004 - vol.28 - n°11 555
de la distance moyenne (euclidienne,
de Chanfrein) entre les points à met-
tre en correspondance [7]. L’utilisa-
tion de points de repère est le plus
souvent couplée à une transforma-
tion linéaire [8].
Les repères utilisés peuvent être ex-
ternes au sujet ou intrinsèques.
Les rLes r
Les rLes r
Les repèrepèr
epèrepèr
epères ees e
es ees e
es exterxter
xterxter
xternesnes
nesnes
nes
On se sert de marqueurs qui peuvent
être remplis de liquide pour assurer
leur visibilité dans les différentes
modalités [9]. En neurochirurgie, les
marqueurs sont attachés à des cadres
stéréotaxiques fixés dans l’os. Ces
cadres étant nécessaires pour l’opé-
ration, les marqueurs, utiles pour la
localisation et le guidage, ne consti-
tuent pas une charge supplémentaire
pour le patient [7, 8]. La chirurgie du
cerveau utilise également des mar-
queurs directement vissés dans l’os,
technique employée pour le posi-
tionnement en radiothérapie et pour
l’orthopédie. Par contre, l’utilisation
de marqueurs collés sur la peau est
non invasive, mais diminue la préci-
sion du fait des mouvements possi-
bles de la peau. Cet écueil est con-
tourné pour les applications en radio-
thérapie par l’utilisation de moules
uniques de contention, employés sur
chaque système d’imagerie (IRM,
TDM, TEP) et sur le système de traite-
ment.
Les rLes r
Les rLes r
Les repèrepèr
epèrepèr
epères intres intr
es intres intr
es intrinsèquesinsèques
insèquesinsèques
insèques
Ils sont constitués de caractéristiques
particulières extraites des données,
caractéristiques qui peuvent être ana-
tomiques : on utilise alors des points
de la morphologie que l’on peut si-
tuer avec précision et qui sont le plus
souvent identifiés interactivement par
l’utilisateur. On peut se servir égale-
ment de données géométriques, con-
sistant à extraire automatiquement
des optima de fonctions géométri-
ques comme le maximum d’un rayon
de courbure. Enfin, on peut se servir
de l’intensité des voxels : dans ce cas
les images subissent d’abord une
étape de segmentation pour en ex-
traire des courbes, des surfaces ou
des volumes.
Ces méthodes ont prouvé leur effica-
cité et leur robustesse dans le
recalage multimodalité intra-sujet en
utilisant, par exemple, la surface de
la peau, facilement identifiable dans
les images d’IRM, TDM ou TEP, et suf-
fisante pour contraindre le calcul
d’une transformation rigide [1, 10].
Mesure de l’alignement utilisantMesure de l’alignement utilisant
Mesure de l’alignement utilisantMesure de l’alignement utilisant
Mesure de l’alignement utilisant
l’image dans sa totalitél’image dans sa totalité
l’image dans sa totalitél’image dans sa totalité
l’image dans sa totalité
Dans ce type de mesure, basée sur
les propriétés des voxels (“voxel
property based”), les données ne su-
bissent aucune réduction, aucune
segmentation. Ce type d’information
est préféré lorsqu’il est difficile d’ex-
traire des structures communes des
jeux de données. Elle permet aussi
de faciliter l’automatisation du
recalage.
Il existe deux approches distinctes :
l’image peut subir un pré-traitement
pour transformer les intensités en un
ensemble de valeurs associées à une
orientation par la détermination des
axes principaux et le calcul des mo-
ments, ou être utilisée telle quelle. La
première approche ne fournit pas, en
général, de résultats très précis, mais
elle est rapide, automatique, et facile
à implémenter [8]. Dans le dernier cas,
on utilise la distribution des intensi-
tés de l’image pour calculer une me-
sure de similarité ou dépendance sta-
tistique. Parmi celles-ci, le coefficient
de corrélation mesure une dépen-
dance linéaire entre les distributions
en intensité des données, tandis que
le rapport de corrélation mesure une
dépendance fonctionnelle [11, 12]. Le
critère de Woods, lui, est fondé sur
une hypothèse d’uniformité : une ré-
gion d’intensité homogène dans un
jeu de données correspond à une
région d’intensité également homo-
gène dans l’autre jeu de données.
Cette hypothèse à été proposée ori-
ginellement pour répondre au pro-
blème du recalage TEP-IRM [12]. En-
fin, l’information mutuelle utilise le
calcul de l’entropie des images, qui
est une mesure du “désordre” dans la
distribution de la densité de proba-
bilité des intensités des pixels [7, 13,
14, 15]. L’information mutuelle sera
choisie dans les cas où l’on dispose
de peu de connaissances sur la dé-
pendance statistique des données, ce
qui est le cas pour le recalage IRM-
TEMP par exemple.
L’optimisation
!La partie optimisation est un algo-
rithme itératif qui recherche la valeur
maximale de la mesure de qualité
d’alignement, correspondant à la
transformation qui conduit au
meilleur résultat pour le recalage. Le
choix de l’algorithme d’optimisation
a une grande influence sur le résul-
tat du recalage, particulièrement en
ce qui concerne la robustesse de la
technique employée par rapport à la
transformation initiale. On distingue
quatre approches de l’optimisation
[16] :
- Les approches quadratiques ou semi-
quadratiques comprennent la des-
cente de gradient, les méthodes de
Powell, de Newton-Raphson, du
Simplex, ou l’Iterative Closest Point
(ICP) [17]. Une grande partie de ces
techniques est documentée dans [18].
Ces méthodes sont peu robustes et
donc bien adaptées aux problèmes
contraints.
- Les approches stochastiques ou ba-
sées statistiques comme le recuit si-
mulé ou les algorithmes génétiques
sont plus robustes que les premiè-
res mais leurs temps de calculs sont
plus longs.
- Les approches structurelles sont
basées sur l’utilisation d’arbres ou de
graphes. Elles sont bien adaptées aux
cas où les mesures de similarité peu-
vent être formalisées par une struc-
ture hiérarchique.
- Enfin, la recherche de l’optimum
peut se faire interactivement avec
l’utilisateur, par inspection visuelle.
Dans ce cas, on parle d’approche heu-
ristique.
Pour éviter les extrema locaux qui
conduisent à un mauvais alignement
des images, et/ou pour réduire le
temps de calcul, on complète parfois
le processus d’optimisation par une
stratégie particulière. La multi-résolu-
tion, par exemple, consiste à sous-
échantillonner les images et à effec-
tuer ensuite des recalages successifs
en augmentant la résolution pour af-
finer progressivement l’alignement
[19, 20, 21]. Pour éviter les erreurs
de recalage, on peut également asso-
cier des mesures de similarité com-

Fusion d'images en multimodalité
556 Médecine Nucléaire - Imagerie fonctionnelle et métabolique - 2004 - vol.28 - n°11
plémentaires, comme l’information
mutuelle et une mesure basée sur l’in-
formation spatiale comme la mesure
des gradients [22].
LA VALIDATION DU RECALAGE
!La validation est une étape à part
entière de l’implémentation d’une
méthode de fusion. Elle permet de dé-
crire et d’analyser les caractéristiques
de la méthode, de démontrer ses per-
formances, son intérêt clinique po-
tentiel et de la comparer aux métho-
des existantes. Elle consiste en l’étude
de la résolution (liée à l’erreur systé-
matique du processus), de la préci-
sion [21], de la robustesse, de la com-
plexité (degré d’automatisation) et du
temps de calcul.
La validation d’une méthode néces-
site la définition d’un “Gold Standard”,
c’est à dire, pour le recalage, d’une
transformation géométrique et/ou
d’intensité de référence entre les
données de validation à mettre en
correspondance. Les données de va-
lidation peuvent être obtenues par
des simulations numériques [23], des
fantômes physiques plus ou moins
réalistes, ou des données de calcul
réels, c’est à dire par une étape de
recalage basée sur l’utilisation de ca-
dres de stéréotaxie ou de marqueurs
lors des acquisitions [24].
VISUALISATION ET INTERACTION
AVEC LES IMAGES RECALÉES
!Trois approches principales sont
utilisées dans la visualisation de la fu-
sion en pratique clinique :
La superposition d’images
!Il s’agit de calculer une image qui
contient l’information des jeux de
données recalés, par opération arith-
métique sur les intensités des voxels,
codage de couleurs (Figure 2Figure 2
Figure 2Figure 2
Figure 2).
Cependant, l’image affichée ne cor-
respond plus à une modalité réelle,
ce qui peut gêner le clinicien.
Figure 2 - Fusion TDM-scintigraphie au MIBG pour neuroblastome (Centre Léon Bérard, Lyon).
La triangulation
!Cette approche consiste à partager
un curseur 3D entre des modules de
visualisation synchronisés : le curseur
désigne les mêmes coordonnées
dans les images recalées, chacune af-
fichée dans une fenêtre propre (Fi-(Fi-
(Fi-(Fi-
(Fi-
gures 3 et 4gures 3 et 4
gures 3 et 4gures 3 et 4
gures 3 et 4).

Ch. Jégou, A. Bonmartin
Médecine Nucléaire - Imagerie fonctionnelle et métabolique - 2004 - vol.28 - n°11 557
Figure 4 - Fusion IRM-TEP (Philips Medical Systems).
Figure 3 - Fusion TEP (Philips ALLEGRO) et TDM (GE LIGHTSPEED 16)
(Centre Hospitalier Lyon Sud).