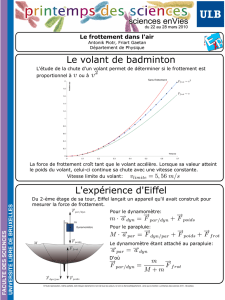
Volant de badminton

Exercice à rendre le vendredi 12 février Langevin–Wallon, PTSI 2015-2016
Volant de badminton
Vous êtes invités à porter une attention particulière à la rédaction et au soin de votre copie. Les numéros des
questions doivent être mis en évidence et les résultats encadrés.
Travailler avec votre cours ouvert et les exercices faits en classe à portée de main est chaudement recommandé.
Utiliser votre calculatrice ou un logiciel comme Geogebra ou Python est possible, et peut parfois vous aider.
Travailler en groupe est autorisé mais le travail de rédaction doit être individuel et le nom des personnes avec qui
vous avez travaillé doit être indiqué au début de votre copie. Les groupes doivent être raisonnables : pas plus de
trois personnes. Je rappelle aussi qu’un travail de groupe est un travail à plusieurs, et pas le travail d’une personne
recopié plusieurs fois.
Le badminton est un sport que vous avez surement pratiqué en cours d’EPS, dans lequel deux joueurs se renvoient
un volant à l’aide d’une raquette. Le but de cet exercice est de proposer une modélisation simplifiée de la trajectoire
du volant sous l’effet conjugué de la pesanteur et de la résistance de l’air, et de confronter ce modèle aux résultats
d’une expérience, donnés par la chronophotographie située en fin d’énoncé.
On assimile le volant à un point matériel. On néglige la poussée d’Archimède dans tout l’exercice, et on néglige
dans un premier temps la force de freinage exercée par l’air.
1 - On lance depuis le sol le volant de masse mavec une vitesse initiale V0dans une direction faisant un angle θ0
avec le plan du sol, supposé horizontal. Déterminer rapidement l’équation de la trajectoire et dessiner son allure.
Déterminer la portée L0(distance horizontale à laquelle le volant retombe sur le sol) en fonction de V0, de θ0et de
l’accélération de la pesanteur g.
2 - Vérifiez l’homogénéité de l’expression de L0obtenue. Vérifiez sa cohérence sur des cas limites simples que vous
choisirez.
3 - La vitesse initiale étant fixée, déterminer sans calcul supplémentaire ou presque l’angle θ0qui permet d’envoyer
le volant le plus loin possible.
On tient maintenant compte du freinage dans l’air, et on modélise la force de freinage par une traînée quadratique
s’écrivant sous la forme
#”
F=−
1
2ρ S Cxv#”
v
où #” vest la vitesse du volant et vsa norme, ρla masse volumique de l’air, Sla surface frontale du volant et Cxun
coefficient phénoménologique appelé coefficient de traînée, traduisant l’effet de la forme géométrique du volant.
4 - Déterminer la dimension du coefficient de traînée.
5 - Écrire l’équation du mouvement du volant pour sa vitesse #” v. Montrer qu’elle admet une solution particulière,
correspondant à un mouvement rectiligne uniforme vertical, dont vous exprimerez la vitesse #” V∞en fonction des
paramètres du problème.
6 - Réécrire l’équation du mouvement en fonction de get de #” V∞.
7 - À quelle condition sur #” vpeut-on négliger le poids du volant ? On suppose que cette condition est initialement
vérifiée. Justifier alors que la trajectoire du volant est rectiligne. Déduire de l’équation du mouvement une équation
différentielle portant sur la norme v. En utilisant une méthode vue dans le chapitre de cinétique chimique (bientôt
le concours blanc !) en déduire que
v(t) = 1
1
V0
+gt
V2
∞
8 - En utilisant cette expression, déterminer et calculer le temps t1/2pour lequel la vitesse est égale à la moitié de
la vitesse initiale. Repérer le point correspondant sur la chronophotographie donnée en fin d’énoncé. Vérifier par une
mesure à expliquer que la vitesse en ce point est approximativement égale à la moitié de la vitesse initiale. Vous
pouvez écrire directement sur la chronophotographie et rendre le sujet avec votre copie.
On peut montrer par un calcul non demandé que la distance horizontale xparcourue lors de ce régime de pesanteur
négligeable en fonction du temps de vol ts’écrit
x(t) = cos θ0
V2
∞
gln 1 + gV0t V2
∞.
1/2 Étienne Thibierge, 4 février 2016, www.etienne-thibierge.fr

Exercice à rendre le vendredi 12 février : Volant de badminton Langevin–Wallon, PTSI 2015-2016
On peut également établir une correspondance entre la distance horizontale xet la norme vde la vitesse du volant,
x(v) = cos θ0
V2
∞
gln V0 v.
9 - On suppose que l’approximation de poids négligeable cesse d’être valable lorsque la composante verticale de la
force de freinage est égale au poids du volant. En déduire d’une part l’expression de và cet instant en fonction de V∞
et θ0et d’autre part la distance horizontale parcourue L.
On modélise la trajectoire complète du volant en distinguant trois régimes successifs :
le régime que l’on vient d’étudier, durant lequel le poids est négligeable ;
un régime intermédiaire ;
un régime limite durant lequel le volant a atteint sa vitesse limite et où son accélération est négligeable.
10 - Localiser sur la chronophotographie le régime limite ainsi défini, en justifiant précisément votre réponse. Vous
pouvez écrire directement sur la chronophotographie et rendre le sujet avec votre copie.
11 - Une première approximation de la trajectoire consiste à oublier la partie correspondant au régime intermédiaire.
Dessiner la trajectoire obtenue dans cette approximation.
12 - Donner l’expression littérale de la portée Ldu tir dans cette approximation. Comment se compare-t-elle à la
portée L0en l’absence de freinage, déterminée à la première question? Estimer Lnumériquement et comparer le
résultat avec la valeur indiquée sur la chronophotographie.
13 - La distance Dparcourue pendant le régime intermédiaire peut dépendre de la masse mdu volant pour prendre
en compte son inertie, de sa vitesse limite V∞pour décrire l’effet des frottements et de l’accélération de la pesanteur g,
qui est l’effet physique à l’origine de la chute. Déterminer par analyse dimensionnelle la dépendance de Den ces trois
paramètres.
14 - On suppose que le préfacteur sans dimension intervenant dans l’expression de Dvaut 1. L’approximation de la
question 11 est-elle justifiée ? Estimer numériquement la portée L0en prenant en compte le régime intermédiaire et
comparer le résultat avec la valeur indiquée sur la chronophotographie.
Fig. 1 –Chronophotographie de la chute d’un volant de badminton. Le volant va de la gauche vers la droite, et
sa position est enregistrée toutes les 50 ms. Le premier point correspond au lancer à t= 0. Figure extraite du blog
scientifique de Baptiste Darbois-Texier, chercheur à l’université de Liège (Belgique). Les vitesses U0et U∞de cette
figure correspondent aux vitesses V0et V∞du texte.
2/2 Étienne Thibierge, 4 février 2016, www.etienne-thibierge.fr