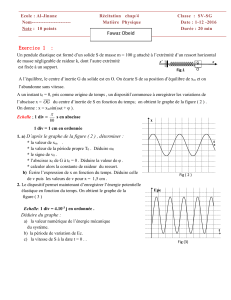
Étude de suites récurrentes I. Cas général

Gaudino, casier 5 version 2.1
Lycée Masséna ´ Etude de suites récurrentes P.C.S.I.834
Le but du T.P. est l’étude des suites récurrentes du type un+1 =f(un). Toute l’étude en Python se fera en flottants.
On rappelle que l’affichage d’un graphe se fait essentiellement avec la commande plot sous la forme :
plot(listes des abscisses, listes des ordonnées)
Plus précisément : pour tracer le graphe de sinus entre 0 et 10
from math import * #on charge le module math
import numpy as np #et tous les modules pour l'affichage
import matplotlib as mp #et oui
import matplotlib.pyplot as plt #tout ça
x = np.linspace(0.,10.) #fabrication automatique des abscisses entre 0 et 10
y = [sin(t) for t in x] #les ordonnées du graphe, par compréhension par exemple
plt.plot(x,y,'r-') #le graphe, avec les options : rouge (r) et trait plein (-)
#on aura besoin aujourd'hui de mettre o à la place de - : affichage de gros points
plt.axhline(color='k') #l'axe x. k pour black...
plt.axvline(color='k') #l'axe y. k pour black...
plt.show() #le show affiche le tout (sans cela, rien n'est affiché)
#comment, c'est déjà fini ?
I. Cas général
1. Déclarer la fonction f:x7→ 2 + ln(x) avec un def.
Dans la suite, on pourra utiliser une facilité propre à Python : une manière rapide de faire cela est de taper :
lambda x: l’expression de la fonction, qui dépend de x(lambda x: est l’analogue de x7→). Plus précisément,
écrire f = lambda x: 2. + log(x).
2. On considère la suite (un)n∈Ndéfinie par : u0= 1 et ∀n∈N, un+1 =f(un). Attention, 1 doit être un flottant
(et donc l’auteur de ces lignes a fait une petite erreur. . .).
(a) Programmer Python de manière à calculer le terme un(la valeur de nsera fixé à 20 pour expérimenter).
On ne demande pas de stocker les résultats intermédiaires. Le corrigé que vous montrera votre prof. est à
considérer comme une question de cours (au programme officiel), à restituer sans délai.
(b) Modifier ce programme de manière à obtenir l’ensemble des points de coordonnées (u0, u1),(u1, u2),...,(un−1, un).
En pratique, on cherchera à avoir les deux listes séparées : celle des abscisses, et celle des ordonnées.
(c) ´ Ecrire les instructions qui permettent à Python de tracer sur un même graphe : la fonction fentre 0,1
(zéro virgule un, et pas 0, qui provoquerait une erreur) et 4 en rouge, la première bissectrice en vert, et ces
points (et les axes) en noirs.
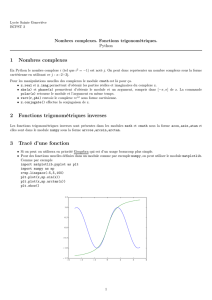
(d) Modifier ce qui précède de manière à tracer non pas ces points mais l’escalier qu’ils constituent : on tracera
les segments qui relient les points (u0,0), puis (u0, u1) puis (u1, u1) puis (u1, u2) puis (u2, u2) . . .
(e) Fabriquer une fonction Escargot qui prend comme paramètre la fonction f, la valeur initiale u0, le nombre
de points à calculer n, l’abscisse minimale xmin du graphe et l’abscisse maximale xmax du graphe, et qui
affiche le graphe sur [xmin, xmax] de la fonction, de la première bissectrice, et de l’escalier.
Cette fonction va permettre la visualisation simple de ce type de suite, en particulier en permettant de
zoomer sur les phénomènes intéressants.
Notez quand même que faire tracer un graphe par une sous-fonction est une mauvaise idée : cette fonction
agit sur son environnement, on parle d’effet de bord, et c’est délicat 1. Si cela pose un problème (suivant
l’évolution des versions de Python), abandonnez la fonction et revenez au code précédent.
(f) Pour ceux qui sont en avance (ceci est donc à faire APR` ES les questions suivantes), on peut raffiner
l’affichage : calculer automatiquement le domaine effectif des x, pour afficher l’escargot complet et la fonction
sans avoir à préciser dans les arguments les valeurs xmin et xmax.
Comprendre également que cette précaution est inutile pour le domaine des y.
3. Regarder le comportement de la suite pour la fonction x7→ 1−cos(x) successivement pour une valeur au choix
de u0>0 puis u0<0.
1. Vous ne savez pas ce que ça veut dire ? Moi non plus, mais dit avec assez d’assurance, ça passe très bien.
1

4. Regarder le comportement de la suite pour la fonction x7→ √1 + xsuccessivement pour une valeur u0= 1 puis
u0= 4.
5. Regarder le comportement de la suite pour la fonction x7→ x+ exp(x) pour u0= 1.
6. Regarder le comportement de la suite pour la fonction x7→ 1 + 1
xpour u0= 1.
7. Regarder le comportement de la suite pour la fonction x7→ 1−x2successivement pour une valeur u0= 0.5 puis
u0= 0.7.
II. Une instabilité numérique
Faire afficher par Python les termes u20 àu30 pour la suite récurrente ∀n∈N, un+1 =|ln(un)|avec les valeurs
initiales u0= 2, puis u0= 2.000000001, puis u0= 2 −0.000000001. On soignera l’affichage, de manière à obtenir un
tableau lisible pour comparer les valeurs.
On doit constater quelque chose vers le 25ème terme.
On peut interpréter cette divergence des valeurs comme liée à l’instabilité numérique liée aux erreurs d’arrondis.
Lorsqu’on remplace xpar une valeur approchée x∗, on ne calcule pas f(x) mais f(x∗) (et encore, on néglige ici l’erreur
liée au calcul de f). Quelle est l’erreur produite ?
|f(x∗)−f(x)|≈|f0(x)||x∗−x|
Ainsi, l’erreur est multipliée par f0(x). L’erreur relative est alors
|f(x∗)−f(x)|
|f(x)|≈|f0(x)||x| |f(x)||x∗−x| |x|
donc est multipliée par |f0(x)||x|
|f(x)|=1 |ln(x)|: c’est une catastrophe quand xest proche de 1 comme ici l’est u24.
III. Suite récurrente double
1. Programmer le calcul du terme nde la suite récurrente double donnée par :
u0=u1= 1 et ∀n∈N, un+2 =un+1 +un
On pourra remarquer que ces termes sont des entiers.
2. Programmer le calcul du terme nde la suite récurrente double donnée par :
u0= 1, u1= 1 −√2 et ∀n∈N, un+2 = 2un+1 +un
et constater le phénomène remarqué 2en cours.
IV. Suite de Syracuse
On souhaite programmer la suite de Syracuse, définie de la manière suivante : u0= 7 et
∀n∈N, un+1 =(un
2si unest pair
3un+ 1 si unest impair
On testera également le comportement pour d’autres valeurs de u0. Dans un premier temps, on souhaite calculer un
pour une valeur donnée de n(n= 10 pour des essais pratiques).
1. Programmer une fonction ftelle que ∀n∈N, un+1 =f(un). Allons-nous travailler en entiers ou en flottants ?
2. Calculer un, pour n= 10.
3. La conjecture de Syracuse affirme (mais personne ne l’a jamais prouvée, c’est pour ça qu’on parle de conjecture
et non de théorème) que quelle que soit la valeur de u0, la suite se stabilisera sur les termes 1,4,2,1,4,2. . .
En admettant que cette conjecture est vraie, programmer le calcul du plus petit entier ntel que un= 1 (ce n
porte le nom poétique de temps de vol). Tester diverses valeurs de u0.
Le nom Syracuse fait référence à une université des U.S.A. (et pas à Henri Salvador). Pour la petite histoire, si vous
arrivez à prouver la conjecture, il y aura au moins deux conséquences : 1) vous deviendrez millionnaire (sans s, mais
en dollars américains, ce qui ne change rien, mais qui fait plus riche) 2) votre nom sera parfois cité par tous les vieux
prof de math de prépa barbus, le jeudi soir vers 17h, à une classe à moitié endormie. C¸ a fait rêver, non ?
2. ou pas suivant l’heure de la sonnerie cette année ! C’est le prof de TD qui va l’expliquer !
2

Lycée Masséna ´ Etude de suites récurrentes (corrigé) P.C.S.I.834
V.
def f(x):
return 2. + log(x)
def Escargot(f,u0,n,xmin,xmax):
u = u0
abscisse = [u]
ordonnee = [0]
for i in range(0,n):
abscisse = abscisse + [u]
u = f(u)
abscisse = abscisse + [u]
ordonnee = ordonnee + [u,u]
plt.plot(abscisse,ordonnee,'ko-') #l'escalier
x = np.linspace(xmin,xmax) #les abscisses des points
y = [f(t) for t in x] #les ordonnées de f
plt.plot(x,y,'r-') #le graphe de f
plt.plot(x,x,'g-') #la bissectrice
plt.axhline(color='k') #les axes x...
plt.axvline(color='k') #et y
plt.show()
#return u
#fin def
Escargot(f,4.,10,0.1,4)
Pour le raffinement, il faut :
– supprimer les arguments xmin et xmax
– calculer le minimum de la liste des abscisses, et affecter sa valeur à xmin.
– calculer le maximum de la liste des abscisses, et affecter sa valeur à xmax.
– cela permet de tracer le graphe de fsur toute la plage. Python fait en fait automatiquement la même chose pour
les abscisses des points.
– Python fait automatiquement la même chose pour les ordonnées.
VI. Suite récurrente double
1. def double(a,b,n):
"""Ne marche que pour n >= 1"""
u,v=a,b
for i in range(1,n):
u, v = v, u+v
return v
print(double(1,1,10))
2. Il suffit de remplacer u, v = v, u+v par u, v = v, u+2*v
VII. Suite de Syracuse
1. Les termes sont tous des entiers.
def f(x):
ifx%2==0:
return x // 2
else:
3

return 3*x+1
#fin def
2. On trouve 10 :
u=7
for i in range(0,10):
u = f(u)
print(u)
3. On trouve n=16.
u=7
n=0
while u != 1:
u = f(u)
n = n+1
#fin while
print(u,n)
4