circuits en régime transitoire ou variable - Jean

Circuits en régime variable
I56.
Les réponses à ce problème doivent être exprimées en fonction des données E, L, r et R,
qui sont indépendantes du temps, ou bien en fonction de grandeurs qui ont été déjà
exprimées en fonction de ces données.
K
R
r
L
E
j
i
u
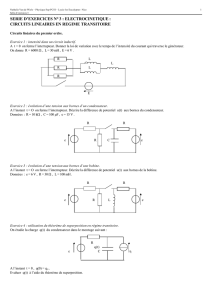
1) L’interrupteur K étant fermé depuis très longtemps, exprimer les valeurs I1, J1 et U1
des courants i et j et de la tension u en régime permanent.
2) L’interrupteur K étant ouvert depuis très longtemps, exprimer les valeurs I2, J2 et U2
de i, j et u en régime permanent.
3) Justifier les propriétés de continuité ou de discontinuité de i, j et u lorsqu’on ouvre ou
ferme K.
4) L’interrupteur K étant fermé depuis très longtemps, on l’ouvre à l’instant 0. Exprimer
i, j et u en fonction du temps t.
5) L’interrupteur K étant ouvert depuis très longtemps, on le ferme à l’instant 0. Exprimer i, j et u en fonction de t.
6) Représenter qualitativement la courbe de u en fonction de t si r = R et si on ouvre et on ferme alternativement K
avec une période T grande par rapport aux temps d’évolution trouvés aux questions précédentes.
7) Même question si r << R.
8) Même question si r >> R.
L
R
C
2
1
II41.
u
10 volts ; 1H ; 20 ; 1 FELRC===Ω=µ
A l’instant 0, on bascule l’interrupteur de la position 1 à la position 2.
1) Déterminer l’équation différentielle satisfaite par la tension u fonction du
temps t. E
2) Déterminer les conditions initiales satisfaites par la tension u fonction du
temps t.
DS : circuits en régime variable, page 1
ω
3) En déduire que , exprimer littéralement et
calculer numériquement .
(cos sin )
t
ue A tB t
λω −
=+
,,,ABλω
4) Calculer la pseudopériode T.
5) Le décrément logarithmique est le logarithme népérien du rapport de deux valeurs de la tension distantes de T.
Calculer-le.
6) On admet qu’on peut observer les oscillations tant que leur amplitude est supérieure à . Quelle est la durée
pendant laquelle on peut les observer ? Combien d’oscillations observe-t-on ?
/10E
A
B
P
K
C
C
R
R
R
III34. Charge de condensateurs.
1) On pose . Quelle est la dimension de ? Que
repésente-t-il concrètement ?
RCτ=τ
2) Si l’interrupeur K est ouvert depuis longtemps, quelles sont
les tensions v1 = v(P) – v(B) et v2 = v(A) – v(M) ? E
3) Même question si K est fermé depuis longtenps.
4) A l’instant 0, on ferme l’interrupteur K, qui était ouvert
depuis longtemps. Quelle propriété de symétrie présente le
montage ? Exprimer les tensions v1 et v2 en fonction du temps
et des données du problème.
IV30. Antiparasitage d’un moteur à courant
continu. M
L = 10 mH ; R = 10 Ω ; E = 1 V.
1) Dans la figure 1, on ouvre l’interrupteur. Que se
passe-t-il ?
2) En réalité, un fil a une certaine capacité, certes
faible, mais non nulle. Un modèle plus réaliste est celui de
la figure 2, où C, capacité de l’interrupteur, est petit, mais
non nul . On ouvre l’interrupteur à l’instant 0. Quel était le
courant auparavant ? Quelles sont les conditions initiales
satisfaites par la fonction q(t) représentant la charge de
l’armature de gauche du condensateur ? Exprimer q(t) ; on utilisera ω défini par 2
2
2
10
4
R
LC L
ω=−>.
figure 2
E C
E L,R L,R
figure 1
3) C = 10 pF . Montrer que le circuit RLC est peu amorti. Calculer la tension maximale atteinte aux bornes de
l’interrupteur.

DS : circuits en régime variable, page 2
V62. i 2R
R
C
2C
v
j
K
u
On pose . RCτ=
Les condensateurs étant déchargés, on ferme K à l’instant 0.
1) Quelles sont les valeurs tout de suite après la fermeture de K des tensions u et
v et des courants i et j ?
2) Quelles sont les valeurs au bout d’un temps infini de u, v, i et j ? E
3) Ecrire les équations satisfaites par u, v, i et j fonctions du temps t.
4) En déduire que l’équation différentielle régissant u(t) est :
2
2
2
45
du du uE
dt
dt
ττ++=
5) Quelles sont les conditions initiales pour u(t) ?
6) Déterminer complètement u(t).
7) Montrer que u(t) est une fonction croissante du temps t.
8) Tracer schématiquement la courbe de u(t).
9) Quel est l’ordre de grandeur de l’instant où u est équidistant de ses valeurs initiale et finale ?
10) Expliquer simplement, sans déterminer v(t), la position relative des
courbes u(t) et v(t). R = 9.105 Ω
K
N
u C = 1
µ
F
E = 100 V
VI58. Lampe au néon.
Une lampe au néon N s'allume quand la tension u à ses bornes dépasse
Va = 60 V ; elle s'éteint quand cette tension devient inférieure à Ve = 20 V.
Allumée, elle équivaut à une résistance r = 105 Ω, éteinte, elle ne laisse pas
passer le courant.
1) L'interrupteur K étant fermé et la lampe éteinte, écrire l'équation différentielle reliant la tension u et le temps t. La
résoudre sans imposer à ce stade de conditions initiales.
2) L'interrupteur K étant fermé et la lampe allumée, écrire l'équation différentielle reliant la tension u et le temps t. .
La résoudre sans imposer à ce stade de conditions initiales.
3) Initialement K est ouvert et le condensateur déchargé. A l'instant 0, on ferme K. Trouver la relation entre u et t.
Calculer l'instant où la lampe s'allume.
4) On choisit cet instant comme nouvelle origine des temps. Trouver la relation entre u et t valable tant que la lampe
reste allumée.
5) Discuter si la lampe s'éteint.
6) Tracer schématiquement le graphe complet de en calculant les durées caractéristiques correspondantes. ()ut
u
VII35.
La résistance non linéaire RNL a pour caractéristique en convention récepteur
, où a est une constante positive. A l'instant 0 , on ferme K, le condensateur
étant déchargé.
3/2
iau=C
RNL
K
E
1) Ecrire l’équation différentielle régissant en fonction du temps t.
()
ut
2) Déterminer la ou les condition(s) initiale(s).
3) Exprimer .
()
ut
VIII48. 10 V 1H 1 F 5 1000ELCrR===µ=Ω=Ω.
uE
C
R
L
r
L’interrupteur étant fermé depuis très longtemps, on l’ouvre à l’instant
0.
1) Montrer que
()
()
2
21
du L du r
LC rC u E
Rdt R
dt ++ ++ =.
2) Montrer que et
()
00u=
()
0
du E
dt rC
=.
3) Calculer numériquement les racines de l’équation caractéristique sous la forme . j−λ ±ω
4) Résoudre littéralement, en fonction des données, de λ et de . ω
5) Exprimer numériquement .
()
ut
6) Tracer le graphe schématique de . Qu’a-t-il de remarquable ?
()
ut

DS : circuits en régime variable, page 3
R ; 2)
IX58. Circuit avec éclateur, d’après ESTP 1985.
Un circuit est constitué d'un générateur à haute tension de force électromotrice constante
et de résistance interne , d’un interrupteur, d'une résistance
et d'un condensateur de capacité relié en parallèle à un éclateur qui
décharge complètement en un temps très court le condensateur lorsque la tension à ses bornes
atteint la valeur . Jusque l’instant 0, le condensateur est déchargé ; on ferme alors
l’interrupteur.
120 kVE=100 kr=Ω
100 MR=Ω1nFC=
050 kVV=
1) Exprimer littéralement la tension en fonction du temps t et des paramètres du problème entre l’instant 0 et
l’instant T de la première étincelle.
()
ut
2) Calculer littéralement et numériquement T.
3) Tracer schématiquement les graphes et . Quel rôle joue T dans ces graphes pour ?
()
ut
()
it 0t>
4) Calculer littéralement et numériquement la valeur moyenne de i au cours du temps pour . 0t>
5) Calculer la puissance moyenne fournie par le générateur. Que devient cette énergie ?
i
R
uL C r
i1i2i3
E,r
R
C
u
i
X35. Circuit RLC parallèle, d’après petites mines 1993.
Données : E = 6,0 V ; R = 2500 Ω ; r = 1250 Ω ; C =1,0 µF ; L = 20
mH.
1) Depuis un temps très long, jusque , l’interrupteur est
ouvert. Expliquer pourquoi u, i 0t=
1, i2 et i3 sont nuls, même si au départ ils
ne l’étaient pas. E
2) A t = 0, on ferme l’interrupteur. Déterminer u, i1, i2 et i3 juste
après cette fermeture (instant ). 0+
3) Déterminer u, i1, i2 et i3 après un temps suffisamment long pour que le régime permanent soit établi.
4) Etablir les équations reliant u, i, i1, i2, i3 et la charge q2 de l’armature du haut de C.
5) Etablir l’équation différentielle régissant i1(t).
6) Les racines de l’équation caractéristique sont de la forme λ ± jω. Calculer λ et ω.
7) Exprimer i1 en fonction de E, R, ω, λ et t.
8) Calculer la pseudopériode.
9) Définir et calculer le décrément logarithmique δ.
10) On considère que le régime permanent est atteint quand l’amplitude des oscillations a été divisée par 1000.
Calculer le temps nécessaire à l’établissement du régime permanent.
11) Représenter qualitativement le graphe de .
()
1
it
12) Après un temps très long, on ouvre l’interrupteur. Quelle est la quantité d’énergie convertie en chaleur dans la
résistance r lors de l’évolution ultérieure ?
Réponses
I. 1) 111 0/JUEIE=== 22 2
ERE
U
rR rR
== =
++
IJ ; 3) est une fonction continue du
temps ; on ne sait rien de i et u ; 4)
j
()
1exp
ErR
ij
()
1exp
RE r R
rR L
+
⎡⎤
=−−
⎢⎥
+⎣⎦
t
rR L
+
⎡
⎤
== −−
⎢
⎥
+
⎣
⎦ ; ut
;
5) uE ; =E
i ;
R
=
(
exp
E
j
)
rt
L
−
+
rR
= ; 6), 7) et 8) voir corrigé.
II. 1) 2
20
du du
LC RC u
dt
dt ++= ; 2) uE et (0) =(0) 0
du ; 3)
dt =1
10 s
2
R
L
−
==λ et
21
2
11000 rad.s
4
R
LC L
−
=−ω ; AE ; 10 V== 0, 1 V
E
B ; 4) ==
λ
ω
3
26, 28.10 s
T ;
5) ; 6)
−
==
π
ω
0, 063T==δλ ln10 0, 23 s t ; ==
λ36
t
NT
== oscillations observables.
III. 1) τ est un temps ; il représente l’ordre de grandeur de la durée de l’évolution du système ; 2) v1 = v2 = 0 ;
3) vv ; 4) centre d’antisymétrie ;
12
2/3E== 12
2[1 exp( 3 / )]
vv .
3
EtRC
== −−
IV. 1) Étincelle ; 2) E
i ; q ;
R
= =(0) 0 (0)
dq E
dt R
= ; 21
() 1 cos sin
2
Rt
LR
qt CE e t t
RC L
−
⎡
⎤
⎛⎛ ⎞⎞
⎟⎟
⎜⎜
=+−+−
⎢
⎥
⎟⎟
⎜⎜ ⎟⎟
⎜⎜
⎝⎝ ⎠⎠
⎢
⎥
⎣
⎦
ωω
ωω ;
3) 3200 volts
E
RC =
ω.

V. 1) ; et ; 2) ; uv ; 5) et 0uv== 0i=/jER=0ij== E==
()
00u+=
()
00
du
dt
+= ; 6)
() (
exp 4 exp
34
Et t
uE ⎡⎤
=+ −− −
⎢⎥
ττ
⎣⎦
)
; 9) 4 . RC
VI. 1) du
RC u E
dt += ;
()
exp t
uEA RC
=+ − ; 2)
()
1
du R
RC u E
dt r
++ = ;
()
()
exp
rE r R t
uA
rR rRC
+
=+−
+ ; 3)
()
1exp t
uE RC
⎡
⎤
=−−
⎢
⎥
⎣
⎦ ;
()
3ln 1 0, 825 s
a
V
tRC E
=−−= ; 4)
()
()
(
exp
a
rE rE r R t
uV
rR rR rRC
+
=+−−
++
)
; la lampe s’éteint après être restée allumée
5ln 0,145 s
e
a
rE
V
rRC rR
trE
rR
VrR
−+
=−=
+−+
;
6) entre deux éclairs, la lampe reste éteinte
pendant la durée
6ln 0,624 s
e
a
EV
tRC
EV
−
==
− ; période
. 0, 77 s
VII. 1) 3/2 du
au C dt =− ; 2)
()
0uE= ;
3)
()
2
1
u
t
20 V
60 V
0, 82 s 0, 14 s 0, 62 s
0
1
2
uat
C
E
=
+
.
=
DS : circuits en régime variable, page 4
VIII. 3) λ et ; 4)
1
502,5 s−867, 46 rad/sω=
()
()
cos
exp sin
1/ 1/ 1/
EEtEE
ut t
rR rR rC rR
⎡⎛ ⎞⎤
ωλ
⎟
⎜
=+−λ − +−ω
⎢⎥
⎟
⎜⎟
⎟
⎜
++⎝ωω+⎠
⎢⎥
⎣⎦
)
; 5)
( ) () (
[
]
9, 95 exp 502, 5 9, 95 cos 867, 46 2300 sin 867, 46uttt=+−− + ; 6) voir
ci-contre qualitativement. t
0
10 V
u
IX. 1)
()
1exp t uE ; 2)
rRC
⎡⎛ ⎞⎤
⎟
⎜
=−−
⎢⎥
⎟
⎜⎟
⎜
⎝⎠
+
⎢⎥
⎣⎦
()
()
0
ln 1 0, 054 s
V
Tr ; 3) T est la période ; 4) RC E =−+−=
04
9, 3.10 A
CV
iT
−
== ; 5) 111WpEi== .
X. 2) ii ; 3) ; 4)
13 2
00 /u iER== = = 0=
123
/0iERii u===
21
i
t
3
qd
uERi ri L
Cd
=−== = ; 2
2
dq
dt
=3
i i=++
i ; ii ; 5)
12
()
211
1
2
11di di E
LC L i
Rrdt R
dt ++ +=
; 6)
et ; 7)
1
600 s− λ=1 7046 rad.s− ω=
()
()
11exp cos sin
E
itt
R
λt
⎡
⎤
=−−λ ω+ω
⎢
⎥
ω
⎣
⎦
4
2/ 8,92.10 s
−
=πω= ; 8) T ;
9) 20,535
π
δ=λ=
ω ; 10) ln1000 0, 0115 st ; 12)
==
λ
28
25, 8.10 J
2
LE
R
−
= .

Corrigés
I. 1) La tension aux bornes du court-circuit K est nulle : JU .
111
0/EIER===
2) En régime permanent, la tension aux bornes d’une inductance di
L est nulle parce que i est constant.
dt
22 2
ER
IJ U
rR rR
== =
++
E
.
3) L’énergie 2
1
2Lj de la bobine est une fonction continue du temps, aussi est une fonction continue du temps. Par
contre, rien n’impose à i et u d’être des fonctions continues du temps.
j
4) Si t, 0>
()
dj
ijL rRjE
dt
=++=
.
L’équation caractéristique est 0rR
Lp ; la solution générale de l’équation sans second
membre est
r R p L
+
++ = ⇒=−
(
exp rR jA t
L
+
=−
)
. Une solution particulière est E
jrR =+. D’où la solution générale de l’équation
avec second membre
. D’où la solution générale de l’équation
avec second membre
=+
()
exp rR E jA t
Lr
+
=−++R
.
La condition initiale est
()
1
00 E jJ A
rR
==⇒+=
+0
. D’où :
() ()
1exp 1exp
ErRREr
ij t u t
rR L rR L
++
⎡⎤⎡⎤
== −− =−−
⎢⎥⎢⎥
++
⎣⎦⎣⎦
R
5) Les équations sont E
uE iR ==
et
(
0exp
dj rt
)
j jA
dt L
+=⇒=−Lr . avec la condition initiale
()
2
0E jJ
rR
== =
+A, on obtient
()
exp
Er
jrR L =−
+
t
.
DS : circuits en régime variable, page 5
u
t
u
t
E E
RE
rR+
2
E
0
0
u
t
6) 7)
8)
E
0
RE
rR+