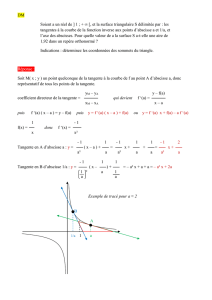
59 Exemple 89. La fonction f : x → x 2 est deux fois dérivable sur R

59
Exemple 89. La fonction f:x�→ x2est deux fois dérivable sur R, et a pour dérivée et dérivée
seconde sur R:
f�(x) = 2x et f ��(x) = 2
Puisque sa dérivée seconde est positive sur R, la fonction fest convexe sur R.
En un point x0où la dérivée seconde f�� d’une fonction fchange de signe, le graphe de cette
fonction traverse sa tangente. Par exemple si f�� est positive avant x0alors fest convexe avant x0
et donc son graphe est au-dessus de ses tangentes, et si f�� est négative après x0alors fest concave
après x0et son graphe est au-dessous de ses tangentes : dans ce cas, le graphe de fest au-dessus de sa
tangente au point (x0, f(x0)) avant x0et au-dessous après, donc il "traverse" sa tangente en ce point.
On donne un nom particulier à ce type de points :
Définition 51. Soit fune fonction deux fois dérivable sur un intervalle I, un point x0de Iest
appelé point d’inflexion de fsi sa dérivée seconde f�� change de signe au point x0.
Exemple 90. Si on considère la fonction sinus sin : x�→ sin(x) alors elle est deux fois dérivable sur
[0,2π] et sa dérivée seconde est sin��(x) = −sin(x) qui change de signe en π: sur [0,π] la dérivée
seconde −sin est négative et donc sin est concave, et sur [π,2π] cette dérivée seconde est positive et
donc sin est convexe. Au point x0=π, la tangente de sin est y= (−1) ∗(x−π) + 0 et le graphe de
sin passe donc de au-dessous de sa tangente à au-dessus :
x
y
y= sin(x)
y=π−x
4.6.5 Tracé du graphe d’une fonction
En vue de tracer le graphe d’une fonction numérique f, on procède selon les étapes suivantes :
— on détermine le domaine de définition de f;
— on calcule les limites de faux bords de son domaine de définition ;
— on étudie les asymptotes éventuelles de fen −∞ et +∞;
— on calcule la dérivée f�et on donne le tableau de variations de f, en faisant apparaitre les
extrema (locaux et/ou globaux) ;
— on calcule la dérivée seconde f��, on étudie son signe pour déterminer les intervalles sur lesquels
fest convexe ou concave, et on trouve les points d’inflexion.
— enfin pour tracer le graphe de fon reporte les asymptotes, les directions asymptotiques, les tan-
gentes horizontales aux points où fatteint un extremum et les tangentes aux points d’inflexion :
on a alors suffisamment d’indications pour tracer l’allure du graphe.

60
On traitera de manière étendue en cours le cas de la fonction Gaussienne f:x�→ e−x2, pour
obtenir le graphe suivant :
x
y
y=e−x2

61
5 Intégrale et primitive
5.1 Intégrale d’une fonction continue
Soit aet bdeux nombres réels tels que a < b, et soit fune fonction continue sur le segment [a, b],
le graphe de f, l’axe des abscisses et les droites verticales x=aet x=bdélimitent une région du plan
(qui peut être en plusieurs morceaux si fs’annule), représentée en gris dans l’exemple ci-dessous :
x
y
y=f(x)
ab
On peut associer à cette région du plan comprise entre le graphe de fet l’axe des abscisses son
aire signée : on dit signée parcequ’on compte en positif l’aire de la zone qui se trouve au-dessus de
l’axe des abscisses, et en négatif la partie qui se trouve au-dessous.
Exemple 91. On considère par exemple le cas a=−1, b= 2 et f(x) = x. L’aire signée de la partie
du plan comprise entre le graphe de f(x) = xet l’axe des abscisses sur [−1,2] vaut alors 3
2:
y=x
x
yl’aire du petit triangle sous l’axe des abscisses est
égale à 1
2, elle est comptée pour −1 2, et l’aire du
grand triangle au-dessus de l’axe des abscisses est
égale à 2, elle est comptée pour +2. L’aire signée
vaut donc −1
2+ 2 = 3 2.
Comme on va le voir, cette aire signée a une grande importance en mathématiques, c’est pour
cette raison qu’on introduit la notion suivante :
Définition 52. Soit aet bdeux nombres réels tels que a < b et soit fune fonction continue sur le
segment [a, b], on appelle intégrale de fsur le segment [a, b]l’aire signée de la partie du plan qui
se trouve entre le graphe de la fonction fsur [a, b]et l’axe des abscisses. On note ce nombre b
a
f(t)dt.
Remarque 40. Par convention on pose a
a
f(t)dt = 0, et si a<balors la notation a
b
f(t)dt désigne
le nombre −b
a
f(t)dt.

62
On déduit les propriétés suivantes de la définition l’intégrale en terme d’aire signée :
5.1. Propriété – Intégrale 1.
Soit a < b et soit fune fonction continue sur le segment [a, b], alors :
— Relation de Chasles : pour tout c∈[a, b] on a
b
a
f(t)dt =c
a
f(t)dt +b
c
f(t)dt
— Intégrale d’une constante : si αest un nombre réel fixé et f(x) = α
pour tout x∈[a, b] alors
b
a
f(t)dt =b
a
αdt =α(b−a)
— Si gest continue sur [a, b] et f(x)≤g(x) pour tout xdans [a, b] alors
b
a
f(t)dt ≤b
a
g(t)dt
En particulier, si met Msont deux constantes telles que m≤f(x)≤M
pour tout x∈[a, b] alors
m≤1
b−ab
a
f(t)dt ≤M
Le nombre 1
b−ab
a
f(t)dt est appelé valeur moyenne de fsur [a, b].
— Lien avec la parité : on suppose a≥0, si fest une fonction paire sur
[−a, a] alors
a
−a
f(t)dt = 2 a
0
f(t)dt
et si fest impaire sur [−a, a] alors a
−a
f(t)dt = 0.
Exemple 92. Si on reprend l’exemple 91, comme f(x) = xalors on a −1≤f(x)≤2 pour tout xdans
[−1,2] et on voit que la valeur moyenne de fsur [−1,2], qui vaut 1
2−(−1) 2
−1
f(t)dt =1
3×3 2=1 2
est bien entre −1 et 2.
Une autre manière de définir l’intégrale de fsur [a, b] est la suivante : on associe à la fonction f
la suite (In)n≥1de terme général
In=b−a
n
n−1
k=0
fa+kb−a
n
Géométriquement, Inest la somme des aires des nrectangles construits à partir de fde la manière
suivante :

63
x
y
y=f(x)
ab
Exemple 93. Si on reprend à nouveau l’exemple 91 on a alors b−a= 2 −(−1) = 3 et on peut
calculer
I1=3
1f−1+0×3 1= 3f(−1) = 3 ×(−1) = −3
I2=3
2f−1+0×3 2+3 2f−1+1×3 2=3 2f(−1) + 3 2f1 2=−3 4
I3=3
3f−1+0×3 3+3 3f−1+1×3 3+3 3f−1+2×3 3
=f(−1)+f(0) + f(1) = 0
In=3
n
n−1
k=0
f−1+k3
n=3 n
n−1
k=0 −1+k3
n
=3
nn−1
k=0
(−1) + 3
n
n−1
k=0
k=3
n−n+3 n
(n−1)n
2=3 2−9 2n
Dans ce cas la suite (In)n≥1est la suite de terme général In=3
2−9 2n.
On peut démontrer que la suite (In)n≥1ainsi définie est toujours convergente, et plus précisément
que sa limite est l’aire signée de la partie du plan qui se trouve entre le graphe de la fonction fsur
[a, b] et l’axe des abscisses : c’est donc l’intégrale de fsur [a, b]. On a alors la propriété :
5.2. Propriété – Intégrale 2.
Soit a < b et soit fune fonction continue sur le segment [a, b], alors :
b
a
f(t)dt = lim
n→+∞
b−a
n
n−1
k=0
fa+kb−a
n
Exemple 94. On reprend l’exemple 91 : dans ce cas, puisque la suite (In)n≥1est la suite de terme
général In=3
2−9 2non voit que sa limite est bien 3 2, qui est effectivement l’aire signée de la partie du
plan comprise entre le graphe de f(x) = xet l’axe des abscisses sur [−1,2].