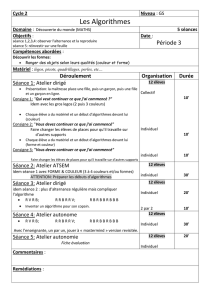
intensionnalité, complétude algorithmique, programma.on et

!"#$"%&'"&($)(*+#&',-./$%0#12*
30*%%*&4-.-%(1*%
5!657&89:&;$)#-0)*<.*-"&=&>?)-%#
9)0@*%A0#?&3-%0A&BA#&6%?#*0.
0)#*)A0$))-.0#?7&($2+.?#"'*&-./$%0#120C"*7&
+%$/%-22-D$)&*#&2$'E.*A&'*&(-.(".
1
1
vendredi 22 octobre 2010

3.-)
•8)#*)A0$))-.0#?7&($2+.*F0#?&G&'"&
H$)(D$))*.&I&.,02+?%-DH
•6$2+.?#"'*&-./$%0#120C"*&G&
")*&)$D$)&'*&(.-AA*&
',-./$%0#12*A&+$"%&.*A&
H$)(D$)A&+%020D@*A&%?("%A0@*A
•6-%-(#?%0A-D$)&'*A&-./$%0#12*A&
0AA"A&'*&2$'E.*A&'*&(-.(".&
A?C"*)D*.
2
Langages
fonctionnels façon de
calculer
Langages
impératifs
intensionnalité
complexité
Langage
fonctionnel
Langage
impératif
Classe
d’algorithmes
Modèle
de calcul
séquentiel
Classe
d’algorithmes
2
vendredi 22 octobre 2010

8)#*)A0$))-.0#?&*#&($2+.*F0#?
'"&H$)(D$))*.&I&.,02+?%-DH
3
3
vendredi 22 octobre 2010

8)#*)A0$))-.0#?&'*A&+%$/%-22*A
4
add1(0,y) = y
add1(S(x), y) = S(add1(x,y))
!""#$#%&'#↦#%('
add2(0,y) = y
add2(S(x), y) = add2(x,S(y))
⟦add1⟧!"#!⊥$%"&!⊥$$'("#!⊥$
⟦add1⟧!"#!)$%"&!)$$'("#*&!⊥$
⟦add2⟧!"#!⊥$%"&!⊥$$'(⊥
⟦add2⟧!"#!)$%"&!)$$'("#*&!)$
⊥
"!⊥$
"+!⊥$
)
"!)$
"+!)$
!"#!$%&'$
()'*)+,,!
-'$./'$$!0
&$#!)()1#+/'$
.',(')#!,!$#
&$#!$%&'$$!0
4
vendredi 22 octobre 2010

propriétés
8)#*)A0$))-.0#?
•JKLLKM&5N&6$.A$)&G&.*&.-)/-/*&'*&0+2)1.3)%&'$2()&,&/4!22.0+%%&53!&-&.-&
+%$+%0?#?&',30/,!2'6%/$+/'$&G&)*&+*%2*#&+-A&'*&(-.(".*%&-.#*%)-D@*2*)#&
A"%&A*A&*)#%?*AN
5
Classe des
fonctions
PR
Langage de
programmation fonctions
0)#*%+%?#-D$)&A"%&.*&
'$2-0)*&'*A&*)D*%A&
+-%*AA*"F
f(0,y) = g(y)
f(S(x), y) = h(x, f(x,y),y)
5
vendredi 22 octobre 2010