+1534)10,-4

Spéciale PSI - Cours "Physique des ondes" 1
Ondes électromagnétiques dans un milieu diélectrique linéaire homogène et isotrope
Chapitre VIII : Ondes électromagnétiques dans un milieu diélectrique
Objectifs :
•Propagation dans un milieu diélectrique linéaire homogène et isotrope
•Dispersion et absorption dans un milieu diélectrique linéaire homogène et isotrope
1. Rappels
Rappels : ”Electromagnétisme” - Electromagnétisme dans les milieux - Chapitre V : Equations de Maxwell dans la matière :
2. Polarisation d’un milieu matériel
2.1. Polarisation dans les milieux isolants
•Dans un milieu conducteur les charges libres ou charges de conduction (électrons ou ions) peuvent se déplacer
dans l’ensemble du matériau. Ce déplacement est à l’origine des densités volumiques de charges libres et de courant libre
jqui intervenaient dans les équations de Maxwell.
•Dans un milieu isolant (ou milieu diélectrique) il n’y a pas de charges libres mais les charges liées peuvent tout de
même se déplacer légèrement. Ces déplacements peuvent provoquer l’apparition de moments dipolaires induits : le milieu
se polarise.
2.1.1. Polarisation électronique ou atomique
2.1.2. Polarisation dipolaire ou polarisation d’orientation
2.1.3. Polarisation ionique
2.2. Vecteur polarisation
Plongé dans un champ électrique, un milieu diélectrique se polarise : chaque volume mésoscopique dde matière acquiert
un moment dipolaire électrique dpinduit par le champ, caractérisé par un moment dipolaire volumique
Pappelé vecteur
polarisation et dé-ni par dp=
Pd.
2.3. Densités de charges équivalentes à la polarisation
2.4. Polarisation variable et courant de polarisation
2.5. Conclusion
Lors de l’étude, à l’échelle macroscopique, du champ électromagnétique dans un milieu matériel, on peut substituer à
la polarisation
Pdumilieu:
•une densité volumique de charges de polarisation p=div
P;
•une densité surfacique de charges de polarisation p=
P.n(nétant orienté vers l’extérieur du milieu matériel);
•une densité volumique de courant de polarisation
jp=
P
ten régime variable.
Ainsi, dans un milieu matériel, nous pouvons utiliser les équations de Maxwell ”dans le vide”, à condition de tenir compte
de ces di2érentes densités volumiques de charges et de courants.
•La densité volumique de charges de polarisation pet la densité volumique de courant de polarisation
jpvéri-ent
l’équation locale de conservation de la charge div
jp+p
t=0
3. Aimantation d’un milieu matériel
3.1. Les di'érents milieux magnétiques
3.2. Action de
Bsur un matériau magnétique
3.2.1. Cas d’une substance diamagnétique
3.2.2. Cas d’une substance paramagnétique
3.2.3. Cas d’une substance ferromagnétique
3.2.4. Vecteurs aimantation
Plongé dans un champ magnétique, un milieu s’aimante : chaque volume mésoscopique dde matière acquiert un
moment dipolaire magnétique d
Minduit par le champ, caractérisé par un moment dipolaire volumique
Mappelé vecteur
aimantation et dé-ni par d
M=
Md.
Certains milieux, appelés milieux ferromagnétiques, peuvent présenter une aimantation permanente.
3.3. Aimantation et distribution de courants équivalents
3.4. Conclusion
Lors de l’étude, à l’échelle macroscopique, du champ électromagnétique dans un milieu matériel, on peut substituer à
l’aimantation
Mdumilieu:
•une densité volumique de courant d’aimantation
jm=
rot
M;
•une densité surfacique de courant d’aimantation
jsm =
Mn(nétant la normale orientée vers l’extérieur du milieu
matériel).
Dans un milieu matériel, nous pouvons utiliser les équations de Maxwell ”dans le vide”, à condition de tenir compte de
la densité volumique de courant d’aimantation.

Physique des ondes. Chapitre VIII : Ondes électromagnétiques dans un milieu diélectrique 2
4. Equations de Maxwell dans un milieux matériels
4.1. Equations pour
Eet
B
•équation de Maxwell-Gauss (M-G) : div
E=+p
0
•équation de Maxwell-Ampère (M-A) :
rot
B=µ0
j+
jp+
jm+µ00
E
t
•équation du Flux magnétique (M-):div
B=0
•équation de Maxwell-Faraday (M-F) :
rot
E=
B
t
Soit en utilisant p=div
P,
jp=
P
tet
jm=
rot
M:
•équation de Maxwell-Gauss (M-G) : div
E=
0div
P
0
•équation de Maxwell-Ampère (M-A) :
rot
B=µ0
j+
P
t+
rot
M+µ00
E
t
•équation du Flux magnétique (M-):div
B=0
•équation de Maxwell-Faraday (M-F) :
rot
E=
B
t
Ces équations ne su7sent pas pour déterminer le champ électromagnétique (
E,
B) car la polarisation
Pet l’aimantation
Mne sont pas en général des fonctions données à priori mais elles dépendent elles-mêmes de
Eet
B.
4.2. Vecteurs
Det
H
On cherche à se ramener à des équations semblables à celles obtenues dans le vide. Pour cela on introduit deux nouveaux
vecteurs :
D=0
E+
Pvecteur induction électrique ou vecteur
D
H=
B
µ0
Mvecteur excitation magnétique ou vecteur
H
4.3. Equations de Maxwell
On obtient alors
•équation de Maxwell-Gauss (M-G) : div
D=
•équation de Maxwell-Ampère (M-A) :
rot
H=
j+
D
t
•équation du Flux magnétique (M-):div
B=0
•équation de Maxwell-Faraday (M-F) :
rot
E=
B
t
L’ensemble de ces quatre équations ne su7t pas à la résolution d’un problème car il faut également connaître les relations
entre
Pet
E(soit entre
Det
E) d’une part et
Met
B(soit
Het
B)d’autre part.
4.4. Théorème de Gauss
D’après l’équation de Maxwell-Gauss, le théorème de Gauss s’applique au champ
Dsous la forme
S
D.d
S=Qint
4.5. Théorème d’Ampère
D’après l’équation de Maxwell-Ampère, le théorème d’Ampère s’applique au champ
Hsous la forme
C
H.d
=S
j.d
S+S
D
t.d
S
4.6. Champs à la surface de séparation entre deux milieux
En tout point Mde la surface S,ilya:
•continuité de la composante tangentielle du champ
E:
ET1=
ET2;
•continuité de la composante normale du champ
B:
BN1=
BN2.
•pour la composante normale de
D:
DN2
DN1=n12;
•pour la composante tangentielle de
H:
HT2
HT1=
jSn12;
en désignant par n12le vecteur unitaire normal à la surface Sen Morienté du milieu 1vers le milieu 2.
4.7. Vecteur de Poynting dans un milieu matériel
Dans un milieu, le vecteur de Poynting
est
=
E
H
Le 9ux de ce vecteur à travers une surface représente le 9ux d’énergie (la puissance) électromagnétique qui traverse cette
surface.
5. Les milieux linéaires, homogènes et isotropes (L.H.I.)
5.1. Permittivité diélectrique d’un milieu matériel
5.1.1. Cas statique
Un milieu est dit linéaire si
Pet
Esont liés par une relation du type
P=0[e]
E

Physique des ondes. Chapitre VIII : Ondes électromagnétiques dans un milieu diélectrique 3
Un milieu est dit isotrope si ses propriétés ne dépendent pas de la direction considérée.
Un milieu est dit homogène si ses propriétés ne dépendent pas du point Moù on se place.
Dans un milieu linéaires, homogènes et isotropes (L.H.I.), lorsque le champ électrique ne varie pas trop vite dans le temps,
les vecteurs
E,
Pet
Dsont liés par les relations :
P=0e
Eet
D=0(1 + e)
E=0r
E=
E
eest un nombre positif (donc sans dimension) appelé susceptibilité électrique du milieu
r=1+eest la permittivité diélectrique relative du milieu (paramètre sans dimension)
=0rest la permittivité (absolue) du milieu et s’exprime en F.m1
5.1.2. Cas dynamique
Si les variations de
Esont trop rapides il apparaît un retard entre la polarisation et le champ électrique.
Dans un milieu linéaire, en régime variable la relation entre
Pet
Eest une équation di2érentielle linéaire.
Dans la suite on suppose que le milieu est linéaire, homogène et isotrope.
Si le champ électrique est sinusoïdal alors la polarisation est, en régime permanent, une fonction sinusoïdale de même pulsation
: il existe un déphasage entre
Pet
Eet l’amplitude de
Ppeut être fonction de la fréquence de
E. On peut alors adopter la
notation complexe et dé-nir une susceptibilité électrique complexe
()=()+i()et
P=0
E
On introduit également la permittivité diélectrique complexe ()=()+i()
5.2. Perméabilité magnétique d’un milieu matériel
5.2.1. Milieux diamagnétiques et paramagnétiques
La plupart des milieux présentent des propriétés magnétiques extrêmement faibles. Ils sont, en général, linéaires, ho-
mogènes et isotropes (L.H.I.). Dans ce cas, les vecteurs
B,
Met
Hsont reliés par
M=m
Het
B=µ0(1 + m)
H=µ0µr
H=µ
H
mest négative pour les milieux diamagnétiques et positive pour les milieux paramagnétiques.
Remarques :
1) La susceptibilité métant très faible, nous écrirons en général, pour un milieu diamagnétique ou paramagnétique
M=m
H=m
µ0µr
B=m
µ0(1 + m)
Bm
µ0
B
2) Dans la matière, le champ
Btotal résulte de la superposition du champ créé par les sources extérieures au milieu
(courants électriques ou aimants) et du champ créé par la matière elle-même (c’est-à-dire les dipôles magnétiques atomiques).
Dans un milieu diamagnétique ou paramagnétique, ce dernier champ est souvent négligé et l’on suppose
Bµ0
H.
5.2.2. Milieux ferromagnétiques
2. Propagation d’ondes dans un milieu LHI
2.1. Onde monochromatique dans un diélectrique lhi
Soit un milieu diélectrique lhi non magnétique.
En régime dynamique nous ne pouvons écrire de façon simple le lien général entre
D(t)et
E(t): la polarisation
P(t)dépend
de la valeur du champ
E(t)à l’instant tmais aussi aux instants antérieurs (cf. rappel § 5.1.2.).
Pour des champs monochromatiques nous pouvons écrire une relation de proportionnalité entre
Det
Eavec une constante
diélectrique ()dépendant de la pulsation.
Nous cherchons alors des solutions des équations de Maxwell sous la forme :
E(M,t)=
E(M)ejtet
B(M,t)=
B(M)ejt
Avec les hypothèses précédentes :
D=()
E
Les équations de Maxwell dans un tel milieux s’écrivent :
div
D=0;
rot
B=µ0
D
t;div
B=0;
rot
E=
B
t
nous obtenons :
div ()
E=0;
rot
B=µ0
()
E
t;div
B=0;
rot
E=
B
t
div
E=0;
rot
B=µ0()
E
t;div
B=0;
rot
E=
B
t

Physique des ondes. Chapitre VIII : Ondes électromagnétiques dans un milieu diélectrique 4
Nous retrouvons les mêmes équations que pour la propagation d’ondes électromagnétiques dans le vide mais en remplaçant
0par ()=0r().
Dans un milieu diélectrique linéaire, homogène et isotrope (LHI), le champ électromagnétique d’une
onde monochromatique véri6e l’équation d’onde de d’Alembert :
Er
c2
2
E
t2=
0et
Br
c2
2
B2
t2=
0
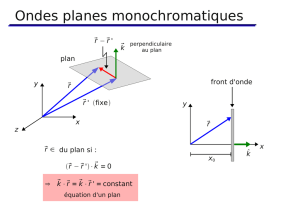
2.2. Onde plane progressive monochromatique dans un diélectrique lhi
Pour une onde plane progressive monochromatique se propageant suivant (Ox):
E(M,t)=
Eej(kxt)et
B(M,t)=
Bej(kxt)
Les équations de Maxwell s’écrivent :
Maxwell-Gauss (M-G) :
k.
E=0 Maxwell-Ampère (M-A) :
k
B=r
c2
E
Flux magnétique (M-):
k.
B=0 Maxwell-Faraday (M-F) :
k
E=
B
Nous retrouvons les mêmes équations que pour la propagation d’ondes électromagnétiques planes progressives monochro-
matiques dans le vide mais en remplaçant 0par ()=0r().
Dans un milieu diélectrique linéaire, homogène et isotrope (LHI), le champ électromagnétique
d’une onde plane progressive monochromatique est transverse : les vecteurs ux,
Eet
Bforment
un trièdre trirectangle direct
B=k
ux
E.La relation de dispersion est k2=r2
c2.
2.3. Modèle de l’électron élastiquement lié
Nous recherchons une expression de la permitivité diélectrique d’un milieu. Nous utilisons pour cela le modèle de l’électron
élastiquement lié :
2.3.1. Hypothèses
•Nous étudions l’action d’une onde électromagnétique sur un atome.
Nous ne considérons que l’action du champ électrique sur les électrons (le noyau dont la masse est beaucoup plus
importante est supposé immobile).
En-n nous supposerons le champ électrique incident uniforme à l’échelle de l’atome (#µmd0,1nm):
E=
E0cos t
•Nous étudions le cas particulier d’un atome à un électron. Soit Ple barycentre des positions successives de l’électron.
Nous a2ectons à ce point Pla masse met la charge q=ede l’électron.
•Au repos, le point Pest confondu avec le noyau repéré par le point O. Hors équilibre, nous notons rle vecteur
OP.
•Nous pouvons interpréter les phénomènes expérimentaux en postulant que le mouvement de Pobéit à l’équation
di2érentielle d’un oscillateur harmonique amorti :
—l’électron est soumis à une force de rappel (de type ressort) de la part du noyau :
Frappel =k
OP =m2
0
OP =m2
0r
—l’électron est soumis à une force de type frottement visqueux (lors de son déplacement, l’électron rayonne une
énergie électromagnétique prélevée sur son énergie mécanique) :
Fvisq =hd
OP
dt =m0
Q
d
OP
dt =m0
Q
•
ravec Qfacteur de qualité

Physique des ondes. Chapitre VIII : Ondes électromagnétiques dans un milieu diélectrique 5
2.3.2. Mise en équation
Appliquons la deuxième loi de Newton : ma=
F
m
••
r=
Frappel +
Fvisq +q
E
m
••
r+m0
Q
•
r+m2
0r=q
E
Nous nous intéressons uniquement au régime sinusoïdal forcé. L’excitation étant sinusoïdale nous utilisons la notation
complexe :
E=
E0cos t
E=
E0ejtet r=r0ejt
L’équation di2érentielle s’écrit alors :
m2r0jm0
Qr0+m2
0r0=q
E0r0=q
m2
0m2jm0
Q
E0=
q
m2
0
1
02j1
Q
0
E0
2.3.3. Polarisation en régime sinusoïdal
Le déplacement rde la charge qengendre un moment dipolaire induit :
p=qr
Par dé6nition, la polarisabilité électronique complexe )est la grandeur telle que :
p=0)
Elocal 0)
E(pour les milieux peu denses)
Nous avons donc :
0)
E=q
q
m2
0
1
02
j1
Q
0
E)=1
0
q2
m2
0
1
02
j1
Q
0
Soit Nle nombre de charges liées par unité de volume. Le vecteur polarisation
Pest alors
P=Np=N0)
E
comme
P=0
E
=N)=
Nq2
m02
0
1
02
j1
Q
0
La susceptibilité diélectrique du milieu s’écrit
=0
1
02
j1
Q
0où 0=Nq2
m02
0
est la susceptibilité diélectrique statique
Soient
=e=0
1
02
12
2
02+
Q02et =m=0
Q0
12
2
02+
Q02
Nous pouvons tracer et en fonction de x=/0(avec Q=10):
-4
-2
0
2
4
6
8
10
0.511.522.53
x
-4
-2
0
2
4
6
8
10
0.511.522.53
x
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
1
/
13
100%