03 - Problèmes à un degré de liberté

PCSI CHAPITRE 3 : PROBLEMES A UN DEGRE DE LIBERTE 1/13
CHAPITRE 3 : PROBLEMES A UN DEGRE DE LIBERTE
I. INTRODUCTION
Nous appliquerons dans ce chapitre les résultats du chapitre 2 à l’étude de problèmes simples
n’ayant qu’un seul degré de liberté, et pouvant donc être décrits à l’aide d’une seule coordonnée.
Les équations étudiées seront donc scalaires et non plus vectorielles.
Nous introduirons pour ce faire les notions d’énergie potentielle et d’énergie mécanique qui sont
d’une grande utilité dans le traitement de nombreux problèmes en physique.
II. ENERGIE POTENTIELLE
1) Energie potentielle et forces conservatives
Il arrive fréquemment que le travail exercé par une force soit indépendant du chemin Γ suivi par son
point d’application et ne dépende que des extrémités de sa trajectoire. On peut alors écrire :
(
)
(
)
ppAB A B
WWxx δ
Γ
== −
∫EE
où
()
p
x
E est une fonction de la position1, nommée énergie potentielle. Une conséquence
importante est que le travail exercé par une telle force lorsque le point matériel accomplit un
parcours fermé est nul :
0
AB
WW δ
Γ
=
=
∫
Le travail élémentaire peut donc s’écrire dans ce cas sous la forme de l’opposé de la différentielle
de la fonction énergie potentielle :
p
Wd
δ
=
−E
(nous reviendrons plus bas sur le choix conventionnel du signe moins). L’énergie potentielle est
définie à une constante près, sans importance car cette fonction n’apparaît physiquement que sous
forme de différence. En remplaçant le travail élémentaire par son expression, on voit que la force
s’exprime alors comme la dérivée d’une énergie potentielle :
(
)
p
dx
Fdx =− E
C’est par exemple le cas du poids, comme nous le verrons plus bas, et, plus généralement, le cas des
quatre forces d’interactions fondamentales de la physique. De telles forces sont dites conservatives.
1 et éventuellement des caractéristiques intrinsèques du point matériel : masse, charge, qui ne sont pas des degrés de
liberté
2) Exemples
• Energie potentielle de pesanteur
Plaçons nous dans le cas du mouvement d’un point matériel dans un champ
de pesanteur, suivant l’axe vertical Oz, en négligeant les frottements de l’air
(figure 3.1.). Le travail élémentaire exercé par le poids sur le point matériel
s’écrit :
W F dz mg dz
δ
=× = × où z g=⋅ =−ge
g
La force étant constante au cours du mouvement, on en déduit l’expression
de l’énergie potentielle de pesanteur :
Figure 3.1. : Mouvement
vertical dans un champ
de pesanteur
A
z
B
g

PCSI CHAPITRE 3 : PROBLEMES A UN DEGRE DE LIBERTE 2/13
(
)
(
)
(
)
pp
Wdmgz d z z mgz δ ==−⇒=−EE
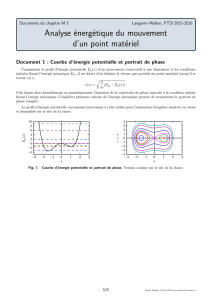
en choisissant la constante nulle pour une altitude nulle. On remarque que l’énergie potentielle de
pesanteur
p
E est une fonction linéaire de l’altitude z et que, plus l’altitude est grande, plus
p
E est
élevée (figure 3.2.a.).
Ainsi, si, comme sur le schéma, on passe de A à B avec BA
zz>, la variation d’énergie potentielle est
positive (
p
E augmente) :
()
(
)
(
)
pp 0 BA
BAmgzz
−
=− − >EE
Le travail fourni par le poids est alors résistant : le poids « lutte » contre le déplacement.
Au contraire, si le point d’arrivée est à une altitude plus basse que le point de départ, l’énergie
potentielle diminue et le travail exercé par le poids est moteur.
Dans tous les cas, il est important de voir que seules les extrémités de la trajectoire ont une importance
dans le calcul de la variation d’énergie potentielle (et donc dans le travail fourni au point matériel). Peu
importe que le point matériel soit allé directement de A à B ou bien qu’il ait fait du « yo-yo » au cours
de son déplacement.
Figure 3.2.a. : Profil d’énergie potentielle de pesanteur
point matériel de masse m = 1 kg, avec g= -10 m.s-2
Figure 3.2.b. : Profil d’énergie potentielle élastique
point matériel fixé à un ressort de longueur x0=5cm et
de raideur k = 3N.m-1
• Energie potentielle élastique
Plaçons nous dans le cas du mouvement rectiligne d’un point matériel fixé à un ressort de raideur k.
Dans la limite d’élasticité du ressort, la force de rappel est proportionnelle au déplacement par rapport
à la position d’équilibre 0
x
, la constante de proportionnalité étant égale à k (figure 3.3.).
Figure 3.3. : Masse fixée à un ressort élastique
On voit qu’on peut exprimer le travail élémentaire comme l’opposé de la différentielle d’une fonction
« énergie potentielle élastique » :
() ()
()
()
22
00
0p
22
WFdx k dx d x
kx x kx x
xx
δ =× =− × =− ⇒ =
⎛⎞
−−
−⎜⎟
⎜⎟
⎝⎠
E
p
ε
(J)
x (m)
x
0
x
m
x
0
(
)
0x
kx x=− −Fe
(m)
p
ε
(J)

PCSI CHAPITRE 3 : PROBLEMES A UN DEGRE DE LIBERTE 3/13
(la constante étant choisie nulle pour une longueur de ressort égale à sa longueur au repos). La force de
rappel élastique est donc conservative et le profil d’énergie potentielle correspondant est parabolique
(figure 3.2.b.).
III. ENERGIE MECANIQUE
1) Définition
Appliquons le théorème de l’énergie cinétique au mouvement d’un point matériel soumis à une
force conservative :
(
)
cpcp
0dWd d δ ==−⇒ +=EEEE
Il apparaît donc naturellement une nouvelle fonction appelée énergie mécanique, notée M
E, égale à
la somme de l’énergie cinétique et de l’énergie potentielle :
Mc p
≡
+E E E
Ceci justifie à posteriori notre choix conventionnel du signe moins dans la définition de l’énergie
potentielle. Lorsqu’un point matériel est soumis à des forces conservatives, son énergie mécanique
est donc conservée 2 :
M0d=E ou M0
∆
=E après intégration
où nous comprenons l’origine de l’appellation de force conservative.
Exemple :
Dans le référentiel terrestre supposé galiléen, on lâche à l’altitude 0 z, sans vitesse initiale, un objet
de masse m et on néglige les frottements de l’air. On assimile l’objet à un point matériel.
Appliquons la conservation de l’énergie mécanique au point matériel pendant sa chute libre, alors
qu’il est à l’altitude 10
zz< (la verticale est orientée comme sur la figure 3.1.) :
() () () () () ()
()
110MM1 M0 c1 c0 P0 P1
0 2 vgzzzz zzzz∆= − =⇔ − = − ⇒= −EE E E E EE
où, dans la dernière égalité, nous avons utilisé la définition de l’énergie cinétique, la valeur nulle de
la vitesse initiale, l’expression de l’énergie potentielle de pesanteur et où nous avons simplifié la
masse qui apparaissait aux deux membres de l’équation. Nous retrouvons sans surprise
l’indépendance d’un mouvement de chute libre vis à vis de la masse.
A la surface de la Terre, l’intensité de la pesanteur (mesurée algébriquement dans le sens des z
croissants) est g = –10m.s–2. Le point matériel a donc, après 5 mètres de chute libre, acquis une
vitesse -1
110m.sv.
2) Forces non-conservatives
Avant de revenir à un cas plus général, il nous faut nous faire une idée plus précise de ce que
peuvent être des forces non-conservatives sur un exemple. Nous en avons déjà rencontré : il s’agit
des forces de frottements, en tout point opposées à la vitesse et exerçant donc un travail résistant :
0
AB
WW δα
ΓΓ
=
=− ⋅ < ∀Γ
∫∫
vdr
Il est clair que le travail qu’elles exercent sur le point matériel entre deux points A et B dépend du
chemin emprunté pour joindre ces deux points : à vitesse constante, le travail sera plus important si
le trajet est plus long et, pour un trajet de longueur donnée, le travail sera plus important si la vitesse
est plus grande.
2 En physique, actuellement, la conservation de l’énergie totale est un principe (1er principe de la thermodynamique). A
chaque fois qu’il est mis en défaut, on introduit de l’énergie sous une nouvelle forme (travail, chaleur, énergie de masse
…) de manière à ce que l’énergie totale soit conservée.

PCSI CHAPITRE 3 : PROBLEMES A UN DEGRE DE LIBERTE 4/13
3) Théorème de l’énergie mécanique
Plaçons nous maintenant dans le cas général, où les forces appliquées sont quelconques. Dans le
théorème de l’énergie cinétique, séparons les termes des travaux c
W
δ
correspondant à des forces
conservatives et les termes nc
W δ correspondant à des forces non-conservatives, puis introduisons
l’énergie potentielle pour faire apparaître l’énergie mécanique :
(
)
cnc nc nc
cpcp
dWWdW d W δδ δ δ =+ =−+ ⇔ +=EEEE
⇔ nc
M
dW δ =E ⇒ nc
MW∆=E après intégration
La variation de l’énergie mécanique au cours d’un déplacement est donc égale au travail exercé sur
le point matériel par les forces non-conservatives : c’est le théorème de l’énergie mécanique. Ce
résultat n’est qu’une variante du théorème de l’énergie cinétique dans lequel on a fait apparaître
l’énergie potentielle, il n’apporte donc aucune nouveauté au niveau du calcul.
La notion d’énergie, par contre, prend davantage de sens : l’énergie mécanique, propre au point
matériel, n’est modifiée que par l’action de forces non conservatives. Le travail de ces forces non-
conservatives correspond à un échange d’énergie avec le milieu extérieur. Par exemple, dans le cas
des frottements fluides, le point matériel cède de l’énergie au fluide sous forme de chaleur à mesure
qu’il s’y frotte.
4) L’oscillateur harmonique
Nous étudions le système suivant, très important en physique : dans le référentiel terrestre supposé
galiléen, un point matériel de masse m est accroché à un ressort de longueur au repos 0
x
et de raideur
k. Le point matériel coulisse sans frottement sur une tige horizontale (figure 3.3.). Nous écartons le
point matériel de sa position d’équilibre d’une distance
x
∆
vers les x positifs puis nous le lâchons
sans vitesse initiale à la date t = 0. La masse étant contrainte de se déplacer le long de la tige, la
seule force à considérer est la force de rappel élastique et le mouvement n’a qu’un seul degré de
liberté.
La force de rappel élastique étant conservative, on exprime la conservation de l’énergie mécanique :
Mcp
cte
=
+=EEE où 2
c
1
2mx=E et
()
(
)
p
2
0
2
xkx x =− E, soit :
(
)
2
2
0
1
22
mx C
kx x
+
=
−
Les conditions initiales
()
00x=
 et
(
)
0
0
x
xx
=
+∆ permettent de trouver la constante :
22Ckx=∆ . On a donc :
()()
22
2
0
mx k x x k x
+
−=∆
qui est une équation différentielle du premier ordre. Elle devient, en posant 0
X
xx=− et 2
0km
ω =
(0
ω
est la pulsation propre du système) :
()
2
222 2
00
X
Xx ωω
+
=∆
En se souvenant de la relation 22
cos sin 1 θθ
+
= et en tenant compte de la condition initiale
()
00X=
, on obtient immédiatement :
(
)
0
cos
X
xt
ω
=∆ ×
Le mouvement de la masse est donc sinusoïdal, de période 0
22Tmk πω π == (figure 3.4.).

PCSI CHAPITRE 3 : PROBLEMES A UN DEGRE DE LIBERTE 5/13
X
Figure 3.4. : Evolution sinusoïdale de la
coordonnée et de la vitesse
Distances en mètres.
Vitesses en unités de 0
ω
.
Durées en secondes.
-1
100g ; 1cm ; 3N.mmxk=∆= =
Figure 3.5. : Evolution de l’énergie potentielle et de
l’énergie cinétique au cours du mouvement
Energies en joules
Durées en secondes
-1
100g ; 1cm ; 3N.mmxk=∆= =
Il est intéressant de tracer sur un graphique l’évolution temporelle des énergies cinétique et
potentielle (figure 3.5.) : on y voit clairement que l’énergie mécanique reste constante et qu’elle se
trouve alternativement entièrement sous forme potentielle ( ; 0
XxX
=
±∆ =
) puis entièrement sous
forme cinétique ( 0
0 ;
X
Xx ω ==±∆
), le transfert d’une forme à l’autre se produisant dans une
durée 2T.
L’équation du mouvement obtenue ci-dessus et rappelée ici pour mémoire :
()
2
222 2
00
X
Xx ωω
+
=∆
est une équation différentielle du premier ordre qui exprime la conservation de l’énergie mécanique
au cours du mouvement. En prenant sa dérivée temporelle, et en éliminant la solution « parasite »
0
X=
 (introduite lors de la dérivation du théorème de la puissance cinétique), on trouve l’équation
du mouvement du second ordre classique, dite équation de l’oscillateur harmonique, que l’on aurait
obtenue en utilisant la loi fondamentale de la dynamique :
220
mXX kXX
+
=⇒
  2
00XX
ω
+
=
On dit pour cette raison que l’énergie mécanique est une intégrale première du mouvement.
Remarque :
En faisant la moyenne des énergies cinétique et potentielle sur une période, on obtient :