Induction et Courants alternatifs

1!
Induction, AC!
v 7s!
16-17!

2!
Loi de Faraday!
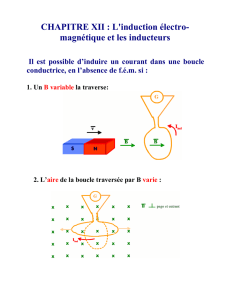
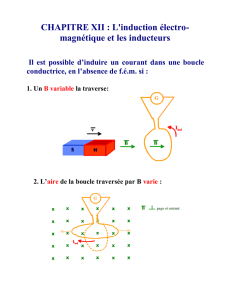
Considérons une boucle plane de
surface A. Si B est constant dans la
boucle:!
€
φ=cosαBA
Une variation du flux peut s'obtenir par!
1) changement de A!
2) de B!
3) de l'angle α, c.à d. de l'orientation de la!
boucle par rapport à B!
La loi de Faraday dit que la Force ElectroMotrice!
(FEM) instantanée vaut!
€
V(t) =−dφ
dt (t)
V!
B!
α" n!
^!
Faraday découvre en 1830 qu' un champ magnétique peut induire!
un courant électrique dans une spire de fil électrique.!
Il constate que la condition nécessaire est que la "quantité" de
champ qui traverse la boucle varie dans le temps.!

3!
Loi de Faraday, loi de Lenz!
R!
I!
n!
^!
Le courant I produit lui aussi un champ magnétique, qui!
est dirigé de façon parallèle à à l'intérieur de la boucle.!
Le courant induit est positif: il tourne!
autour de n selon les aiguilles d'une!
montre.!
^!
n!
^!
Ce courant cherche donc à s'opposer au changement de B,!
donc du flux.!
Loi de Lenz: le champ dû au courant induit s'oppose toujours aux!
modifications du flux.!
Boucle dans un champ B qui va!
en diminuant.!

4!
Générateur électrique!
Boucle de surface A qui!
tourne dans un champ B!
avec vitesse angulaire ω!
€
φ(t) =ABcos(ωt)
€
V=−dφ
dt =ωABsinωt
On produit donc un courant alternatif:!
"alternateur".!
Par des contacts glissants!
on peut rendre le courant!
continu: "dynamo".!
B!
~!
=!
dynamo de Gramme 1870!

5!
Transformateur"
N1 spires!
N2 spires!
primaire secondaire!
Si la totalité du flux est contenue!
dans le "circuit magnétique",!
alors chaque spire voit!
une FEM !
€
δV=−dφ
dt
V1!V2!
Au total, on aura:!
€
V
1=N1δV V2=N2δV
€
V2
V
1
=N2
N1
Ex.: 220V CA à 12V CA: utiliser un rapport de spires 220/12!
donc!
deux enroulements couplés magnétiquement!