Intro : La monnaie est géré par la BCE : Banque Centrale

Intro : La monnaie est géré par la BCE : Banque Centrale Européenne, située à Francfort
(allemands plus attentifs que nous pendant les années 80’s). La BCE créé et gère la
masse monétaire, c’est à dire qu’elle est en charge de la politique monétaire européenne.
Le traité de Maastricht, traité fondateur de l’euro, lui garantie son indépendance
(n’a pas à rendre compte des opérations prises).
La BCE prête cette masse monétaire aux agents financiers, principalement aux
banques commerciales, selon un taux directeur (1er taux d’intérêt) autour de 1%
actuellement.
Puis ces banques commerciales les prêtent elles mêmes à 2 acteurs
économiques : les ménages et les entreprises, à un taux supérieur au taux directeur.
C’est la demande de monnaie qui suscite l’offre monétaire (la création de
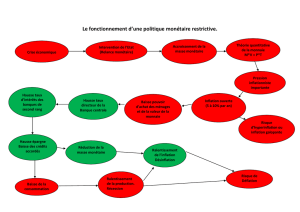
monnaie). Le risque est l’inflation, la BCE se doit donc de réguler la masse monétaire, en
« jouant », en faisant varier le taux directeur. L’ensemble des taux pratiqués dans
l’économie réelle va alors augmenter.
(Plus le crédit sera cher, moins de personnes en demanderont, et inversement ! S’il
n’y a pas assez de demandes, on baisse les taux.)
La BCE exerce la politique monétaire avec un seul objectif : celui de maintenir le
niveau de l’inflation le plus bas possible dans la zone euro.
Pour pouvoir gérer cette masse monétaire, elle doit pouvoir connaître à tout
moment la quantité monétaire en circulation dans son économie. Elle va alors calculer
un certain nombre d’agrégats : M1, M2 et M3, qui déterminent la quantité monétaire en
circulation ; ainsi qu’un agrégat pondéré appelé MP3.
I) Les agrégats monétaires
M1 a pour objectif de mesurer la masse monétaire pleinement liquide, ou quasi
liquide (pièces, billets). Liquidité : prêts à être utiliser immédiatement.
M1 = ensemble des billets + pièces + dépôts à vue (carte bleue + chéquier)
On a l’obligation d’avoir un compte courant, et on ne peut détenir plus de 10 000€ en
liquide. Ce sont les dépôts à vue qui représentent la quasi liquidité.
M2 = M1 + Livrets d’épargne
Le livret d’épargne est un compte rémunéré non bloqué. L’argent est mobilisable
indirectement (transfert sur le compte courant). Cette mobilisation ne remet pas en
cause l’existence de ce compte.
M3 = M2 + Comptes à terme < 2 ans (ou égal) + OPCVM
Un compte à terme est un contrat de placement pour une durée donnée appelée
maturation. Il n’est donc pas possible de mobiliser une partie de ce capital sans casser ce
contrat et donc récupérer la totalité. (Maturation de PEL = 4 ans donc pas compris dans
M3).
OPCVM = Organismes de Placement Collectif en Valeur Mobilière (sociétés de
placement). On en distingue 2 sortes par la taille :
- Les SICAV = Sociétés d’Investissement en Capital Variable (beaucoup plus
conséquente)
- Les FCP = Fonds Communs de Placement
Depuis 1987, on n’a plus un accès direct aux marchés financiers. Les intermédiaires
utilisés sont d’abord les banques, puis surtout ces OPCVM.

On désigne par OPCVM l’ensemble des titres financiers détenus sur les marchés
(actions, obligations d’entreprises….).
MP3 : agrégat pondéré, dans la mesure où il intègre un coefficient de
pondération, nommé alpha.
MP3 = alpha x M3 + alpha (PEL) x PEL + alpha (T) x T
T = bons du trésor, titres publics
Alpha est appelé coefficient de monétarité. Il mesure le degré de liquidité d’un
actif. C’est à dire la part considérée comme liquide de cet actif.
Alpha d’un actif i est compris entre 0 et 1. Et lorsqu’alpha = 1 : 100% de l’actif est
liquide.
Alpha (B=pièces & billets) = 1. Lorsqu’alpha = 0 : l’actif est pleinement non
liquide.
Alpha (O=obligations) = 0 : l’argent investit dans des obligations ne servira
probablement jamais à des transactions, il ne sera donc jamais transformé en liquidité.
L’actif de référence pour le calcul de alpha est l’obligation publique, avec alpha
(O) = 0. Tous les autres alpha(i) seront donc calculés en référence à l’obligation, et
notamment à sa rémunération.
Dès lors, l’alpha d’un actif i est égal à la rémunération de l’obligation –
rémunération de l’actif dont on veut calculer l’alpha / rémunération de l’obligation :
Alpha(i) = Ro - Ri
Alpha(B) = (Ro – Rb) / Ro = Ro / Ro = 1, car Rb =0.
Exemple : Obligations (4%)
Livret jeune (3%)
Calculer l’alpha (livret jeune) = (Ro – Rlj) / Ro = (4-3)/4 = 1/4 = 0,25.
25% de la quantité disponible dans un livret jeune va servir à des transactions.
Alpha(PEL) = (Ro – R(PEL)) / Ro
Exemple : O(5%) et PEL(3% ,50)
Calculer Alpha(PEL) x PEL
Alpha (PEL) = (Ro-R(PEL)) / Ro x PEL = 2 / 5 x 50 = 20.
M3 = M2 + OPCVM + CT = M1 + LE + OPCVM + CT = B + D + LE + OPCVM + CT.
Alpha x M3 = alpha(B) x B + alpha (D) x D + alpha (LE) x LE + alpha (opcvm) x
OPCVM + alpha(ct) x CT
MP3 = Alpha B x B + Alpha D x D + alpha LE x LE + Alpha OPCVM x OPCVM + Alpha CT x
CT + Alpha PEL x PEL + Alpha T x T
Ro

II) Théories de l’offre et de la demande de monnaie
A) Le modèle de Fisher ou la théorie quantitative de la monnaie
Fisher est un économiste Américain qui va proposer une identité mettant en
relation 4 variables macroéconomiques. Ce modèle date des années 20’s.
Qu’est ce qu’une identité ? Une identité mathématique est une égalité
constamment vérifiée, quelque soit la valeur des variables en question.
La première variable est M : Masse monétaire, elle est notamment mesurée par
sa variation d’une période à une autre.
La 2e variable économique est V : Vitesse de circulation de la monnaie : la
masse monétaire se déplace, circule. On peut mesurer V par le temps que met une unité
monétaire émise pour revenir à son émetteur.
Constatant que la première définition est limitée dans la mesure ou bon nombre
de transactions se font de manière dématérialisée, Ficher propose une autre définition, à
savoir :
Le nombre de transactions effectuées par une unité monétaire, dans un espace
économique donné et sur une période donnée.
La 3e variable économique est P : Niveau général des prix, mesuré par le niveau
d’inflation (=conséquence de la hausse générale des prix). L’inflation monétaire est une
perte de valeur de la monnaie, qui se traduit naturellement par une augmentation des
prix.
La 4e variable économique est T : volume des transactions, il s’agit de la somme
des transactions effectuées dans un espace économique donné et sur une période
donnée.
Fisher fait un lien implicite entre la croissance économique et le volume des
transactions T. Il considère que toutes augmentations de richesse dans un espace
économique se traduit par une augmentation des transactions, et dans les mêmes
proportions.
Fisher propose l’identité suivante : M x V = P x T.
Il existe dans ce modèle 2 variables endogènes (à l’intérieur) et 2 variables
hexogènes (à l’extérieur).
Dans l’économie, on a 2 sphères qui coexistent : la sphère dite réelle : sphère de la
production et de l’échange des biens et des services, et la sphère dite monétaire et
financière : sphère des transactions financières et de la circulation de la masse
monétaire. Il s’agit ici de la sphère monétaire.
Il existe 2 variables appartenant à cette sphère monétaire, et 2 variables en
dehors de cette sphère monétaire.
- M est une variable endogène.
- V est observé par la banque centrale et c’est donc une variable hexogène.
- P est mesuré par l’inflation monétaire, et est donc une variable endogène.
- T est une variable hexogène.

Il existe 2 variables observées : V et T. Leurs valeurs stagnent donc on les écrits : V et T.
Ainsi, M x V = P x T  P x M = P.
La monnaie n’est pas une richesse, c’est un vecteur d’échange de la richesse. La
création monétaire ne contribue pas à l’augmentation de la richesse dans un Etat.
Dès 1973, on abandonne petit à petit l’empreint à notre banque centrale.
B) Le modèle de Marshall
C’est un économiste Américain, il est le chef de fil de « l’école de Chicago », contemporain
du XXe siècle. Il critique le modèle de Fisher :
- Il considère que la vitesse de circulation de la monnaie n’est pas une variable qui
induit nécessairement une incidence sur le niveau général des prix. Il considère V
comme une variable muette.
- Il remet en cause le lien implicite entre la croissance économique et le volume
des transactions. Selon lui, toute augmentation de richesse n’induit pas
nécessairement une augmentation du volume des transactions. Marshall
considère par exemple que les stocks enregistrés par les entreprises font la
preuve que toutes richesses ne sont pas nécessairement échangées.
 Marshall propose de remplacer le volume des transactions T par la richesse
produite : la production nationale.
- Marshall considère qu’il y a une variable très importante mais absente du modèle
de Fisher. En effet, il considère que toute offre de monnaie est conditionnée
d’abord par la demande de monnaie.
 Il propose de remplacer T par Y (production nationale = PIB). Il introduit
également une autre variable qu’il nomme k = demande de monnaie.
M = k x P x Y : le modèle de Marshall se lit de la façon suivante :
L’offre de monnaie est fonction de la demande de monnaie k, en lien avec la production
de richesse nationale et en lien avec le niveau général des prix.
Remarque : Le plus important dans une économie n’est pas tant la masse monétaire en
valeur absolu, mais bien la masse monétaire qui circule. Elle est d’ailleurs mesurée par
l’agrégat MP3. On peut dès lors discuter, s’interroger sur l’incidence de la variable V.
On peut considérer qu’une variable hexogène est constante : Y.
k est une variable endogène.
M = k x P x Y.
Toute augmentation de la masse monétaire n’aura pas de conséquence directe sur le
niveau de l’inflation monétaire P. Une partie sera absorbée par la demande de monnaie.

C) Le modèle Keynes
C’est un économiste Anglais, contemporain du XXe siècle. Selon lui, il existe 3 motifs de
détention de la monnaie :
- Motif de transaction : les agents économiques désirent de la monnaie pour
effectuer des transactions, pour échanger.
- Motif de précaution : les agents économiques désirent de la monnaie pour faire
face aux aléas de la vie, c’est à dire qu’ils désirent épargner.
- Motif de spéculation : les agents économiques veulent de la monnaie pour
spéculer (acheter pour revendre dans l’objectif de faire des plus valu), et
principalement jouer sur les taux d’intérêts.
Keynes introduit la spéculation dans l’analyse économique et considère que cette
variable est dangereuse pour le système capitaliste.
Dans la mesure ou les comportements spéculatifs donnent naissance
à des bulles dites spéculatives, qui lorsqu’elles sont déconnectées de la réalité : la sphère
réelle, s’effondrent brutalement : c’est ce qu’on appelle un krach.
Le modèle de Keynes est le suivant : M = L1 x Y + L2 x i avec :
L1 : la demande de monnaie, pour des motifs de transaction et précaution.
L2 : la demande de monnaie pour des motifs de spéculation
Y : la production nationale
I : le taux d’intérêt directeur
Le modèle se lit de la façon suivante :
L’offre de monnaie est fonction de la demande de transaction et de précaution en lien
avec la richesse produite + la demande de spéculation en lien avec le taux d’intérêt.
La relation entre L2 et I est inverse : lorsque I augmente, L2 diminue et inversement !
D) Modèle de Baumol
Baumol critique le modèle de Keynes et considère que la demande de monnaie L1
dépend également du taux d’intérêt i, ce qui n’apparaît pas dans le modèle de Keynes.
Baumol propose un modèle ou il s’agit de raisonner sur un individu.
D’après Baumol, si l’agent décide de placer son encaisse, il va subir un coût de
transaction. Le placement se fait au taux d’intérêts i. Ce coût de transaction, il le subit
notamment lorsqu’il désire transformer son encaisse de placement en encaisse de
transaction. Ces coûts correspondent notamment à des frais divers ou à des taxes.
C
1
0
Période
Encaisse
C/2
1/2