MouveMent d`un projectile dans un chaMp de pesanteur uniforme

Filière : Physique-chimie CRMEF –Fès- 2012-2013
Encadré par : Pr. L. KADIRA
1
MouveMent d’un projectile dans un chaMp de
pesanteur uniforme
Objectifs :
 Savoir appliquer la 2ème loi de Newton.
 Etablir l’équation de la trajectoire d’un projectile dans un champ de pesanteur.
 Visualiser la trajectoire d’un projectile dans le champ de pesanteur terrestre. Comparer
les résultats des mesures réalisées à partir d’un enregistrement vidéo du mouvement
avec les paramètres déterminés par étude théorique.
 Modéliser une trajectoire et les vecteurs-vitesse et accélération au cours du mouvement.
Matériel
 Balle de tennis
 Règle et niveau
 Webcam et logiciels AVIMECA2, REGRESSI
 Logiciel de simulation numérique Maple
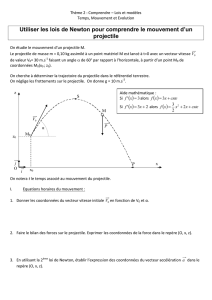
I- Etude théorique
On étudie le lancer d’un projectile, de masse m et de centre d’inertie G avec une vitesse
initiale
0
V
dans un champ de pesanteur uniforme (lancer au voisinage de la terre).

Filière : Physique-chimie CRMEF –Fès- 2012-2013
Encadré par : Pr. L. KADIRA
2
1- Appliquer la 2 éme loi de Newton à la balle dans le champ de pesanteur terrestre uniforme
en supposant que la poussée d’Archimède et les forces de frottement sont négligeables par
rapport au poids.
2- Montrer que le mouvement est plan et que l’on obtient pour :
 le vecteur-accélération
0
0
x
Gy
z
a
aa
ag
 Le vecteur- vitesse
 Le vecteur- position
3- Etablir l’équation y = f(x) de la trajectoire à partir des équations horaires paramétriques.
4- La flèche de la trajectoire est l’altitude maximale atteinte par rapport au point de
lancement. Elle correspond donc ici à z(tF). montrer que :
5- La portée est la distance entre le point de lancement O et le point d’impact P sur le plan
horizontal contenant O. Elle correspond donc ici à xP. montrer que :
6-Calculer toutes les valeurs numériques (des questions 2, 3, 4 et 5) pour la valeur de
V0=6,07m.s-1 et de α=68,03° à fin de les comparer à celles obtenues par modélisation.

Filière : Physique-chimie CRMEF –Fès- 2012-2013
Encadré par : Pr. L. KADIRA
3
II. Etude Expérimentale
II.1. Etude via les logiciels AVIMECA2, REGRESSI
II.1.1 Pointage vidéo
A l’aide d’une webcam , réaliser l’enregistrement d’une balle de tennis lancée
obliquement. On dispose alors d’un fichier vidéo numérique au format avi et on exploite cet
enregistrement avec le logiciel Aviméca, A défaut, on utilisera une vidéo déjà prête.
 Lancer Aviméca. Puis faire Fichier, Ouvrir… Aller chercher le fichier .avi désiré
 Agrandir l’image en cliquant sur Adapter
 Aller dans l’onglet Etalonnage
- cliquer sur l’onglet Etalonnage, sélectionner un système d’axe,
- Choisir échelles identiques : entrer une distance connue entre deux points
donnés.
 Aller dans l’onglet Mesure
- pointer les positions successives de la balle.
 Une fois le pointage achevé, lancer Régressi depuis Aviméca
II.1.2. Modélisations
II.1.2.a. Equations horaires paramétriques
1- Tracer x(t). Quelle est l’allure de la courbe ? Relever le modèle proposé par le logiciel
(type et valeurs numériques). A quoi correspond le coefficient directeur de la fonction linéaire
x(t) ?
2- Tracer y(t). Quelle est l’allure de la courbe ? Relever le modèle proposé par le logiciel
(type et valeurs numériques).
II.1.2.b. Coordonnées du vecteur-vitesse
1- Tracer vx(t). Quelle est l’allure de la courbe ? Relever le modèle proposé par le logiciel
(type et valeurs numériques). Comparer la valeur au coefficient directeur de la fonction x(t).
Que vaut l’accélération suivant l’horizontale ? Qualifier le mouvement suivant l’horizontale.
2- Tracer vy(t). Quelle est l’allure de la courbe ? Relever le modèle proposé par le logiciel
(type et valeurs numériques). A quoi correspond le coefficient directeur de la fonction linéaire
vy(t) ? Quelle valeur devrait-on retrouver ? Qualifier le mouvement suivant la verticale.

Filière : Physique-chimie CRMEF –Fès- 2012-2013
Encadré par : Pr. L. KADIRA
4
3- A quelle date a-t-on vy = 0 m.s-1 ? Comparer le sens des vecteurs
a
et
v
(en fait, il suffit de
comparer ici les signes de ay et vy) et en déduire la nature du mouvement avant et après cette
date.
II.1.2.c. Equation de la trajectoire
1- Tracer y(x). Quelle est l’allure de la courbe ? Relever le modèle proposé par le logiciel
(type et valeurs numériques).
2- A l’aide du curseur réticule relever sur la trajectoire modélisée la valeur de ymax
(correspondant à la flèche), et celle de xmax (correspondant à la portée).
II.2. Etude via Logiciel de simulation numérique Maple.
1- Déclarer tous les paramètres du problème comme des variables globales.
2- Déclarer trois variables eqx, eqy et eqz et leur affecter respectivement les équations du
mouvement selon
x
e
,
y
e
,
z
e
.
3- Déclarer les conditions initiales CIx, CIy et CIz associées aux équations précédentes.
4- Résoudre les équations différentielles du mouvement et extraire les expressions de x(t), y(t)
et z(t).
5- Transformer les expressions x, y et z en fonction afin de pouvoir les manipuler
6- Affecter des valeurs numériques aux paramètres du problème
7- Déterminer via Maple l’instant tF d’impact du projectile sur le sol.Faire calculer alors la
portée xP du tir.
8- Tracer la trajectoire z = f(x) entre la position initiale et le point d’impact.se fait avec la
commande odeplot et se charge via l’instruction with(plots).
9-déclarer plusieurs valeurs d’angle de tir. Observer son influence sur la portée et la flèche.

Filière : Physique-chimie CRMEF –Fès- 2012-2013
Encadré par : Pr. L. KADIRA
5
Correction
I- Etude théorique
On étudie le lancer d’un projectile, de masse m et de centre d’inertie G avec une vitesse
initiale
0
V
dans un champ de pesanteur uniforme (lancer au voisinage de la terre).
I.1- Quelles sont les équations horaires du mouvement ?
 Système d’étude :(Projectile)
 Référentiel d’étude : Toujours définir rigoureusement le référentiel dans lequel sera
effectué l’étude. Prendre garde à ne pas changer implicitement de référentiel durant
l’étude. Le référentiel est terrestre supposé galiléen.
 Bilan des forces s’exerçant sur le système :
- poids
P
du projectile.
- poussée d’Archimède
A
.
- les forces de frottements de l’air (frottement fluide) :
f
proportionnelle à la
vitesse du projectile.
Choisir une base de travail et projeter les forces sur les vecteurs de cette base : ici la base
cartésienne (
x
e
,
y
e
,
z
e
).
On supposera qu’on peut négliger
A
(la masse volumique de l’air est très faible devant celle
du projectile), et
f
(la vitesse initiale du projectile et la distance parcourue suffisamment
faibles) devant
P
On pourra donc considérer que le mouvement du projectile est un
mouvement de chute libre dans un champ de pesanteur uniforme.