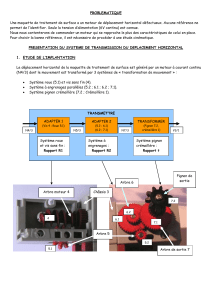
Moment d`une force par rapport à un point - TPWorks

Cours
Notion de Moment d'une force par rapport à un point
Mécanique
Moment d'une force par rapport à un point.doc
STS : Conception Industrialisation Microtechniques Page 1 /2
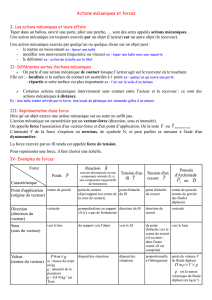
I Définition
On appelle moment, par rapport au point B de la force
2/1
A appliquée au point A, le vecteur d'origine
B défini par la relation :
(
)
2/12/1B
A BA AM ∧= ou
(
)
k A d AM
2/12/1B
r
×±=
- le moment est aussi communément appelé couple
Un moment génère ou interdit un mouvement de rotation autour d'une droite ∆.
On caractérise le moment par :
- son point d'application : B
- sa direction :
perpendiculaire au plan défini par les vecteurs
BA
et
2/1
A
- son sens :
(
)
0 AM
2/1B
≥ sens du vecteur vers
k
r
(
)
0 AM
2/1B
≤ sens du vecteur vers
k
-
r
- sa norme :
(
)
α sin A BA AM
2/12/1B
××=
(
)
A d AM
2/12/1B
×=
(
)
(
)
k N j M i L AMavec NML AM
AAA
2/1B
2
A
2
A
2
A
2/1B
r
r
r
++=++=
- le moment est symbolisé comme vecteur par une flèche à double trait :
L'unité légale du moment est le newton-mètre, son symbole est N.m (on utilise aussi le mN.M = N.mm)
- sens du moment dans repère O,x,y,z
positif x vers y, négatif y vers x
II Rappel sur le produit vectoriel
( )
ABAABA
ABAABA
ABAABA
A
A
A
BA
BA
BA
2/12/1
B
X . y- Y.x Z . x-X .z Y.z -Z . y Z
Y
X
z
y
x
A BA AM =∧=∧=
III Résultante des moments
Soit
R
la résultante des forces (somme vectorielle des n forces s'exerçant sur le solide considéré ), le
moment résultant en n'importe quel point I des n forces est égal au moment en I de la résultante
R
.
Nota : lorsque le solide est en équilibre la résultante des moments est égale à zéro.
( ) ( ) ( ) ( ) ( )
( )
( ) ( ) ( ) k NNj MMi LL RM alors
N
M
L
BM et
N
M
L
AMavec BMAM RM Si
BABABA
I
B
B
B
3/2I
A
A
A
1/2I3/2I1/2II
rrr
+++++=
+=
d : longueur du segment
orthogonal au support de
2/1
A et passant par B
∆
α
2/1
A
(
)
2/1B
AM
A
B
d
O
z
y
x
A
+
B
d
2/1
A
O
y
x
(
)
0 AM
2/1B
≥
A
-
2/1
A
d
O
y
x
B
(
)
0 AM
2/1B
≤

Cours
Notion de Moment d'une force par rapport à un point
Mécanique
Moment d'une force par rapport à un point.doc
STS : Conception Industrialisation Microtechniques Page 2 /2
IV Actions mécaniques dues à un système pignon crémaillère
Lors de son mouvement de translation la
crémaillère 2 génère une action
mécanique de contact
2/1
A inclinée d'un
angle de pression α (en général α = 20°)
Cette force crée en O un moment ou
couple dans le pignon 1 :
(
)
2/12/1O
A OA A M ∧=
Ou bien algébriquement :
(
)
2/1
2/1O
.A d A M += avec
2/1
A d ⊥
Ce moment génère la rotation du pignon 1.
V Actions mécaniques dues un moteur électrique
Au cours du fonctionnement, le stator 1 exerce sur
le rotor 2 des actions mécaniques
i
f
r
; elles se
réduisent à un couple moteur C
m
suivant l'axe x.
Le moment en un point O quelconque de l'axe x
s'écrit : i C M m
O(1/2)
r
=
Ce couple moteur est déterminé par la relation
d'énergétique suivante :
P = C
m
.ω
2/1
P : puissance du moteur (en W)
C
m
: couple moteur (en N.m)
ω
2/1
: vitesse angulaire (en rad/s)
VI Actions mécaniques dues un ressort de flexion enroulé
(complément : cf. cours ressorts)
Une force
2/1
B due à une pièce 2 (non représentée)
génère au point A un moment proportionnel à θ l'angle de
rotation du ressort.
Le moment est défini par la relation :
(
)
l . 12
E.b.h
kavec k . k B M
3
aa
2/1A
== r θ
b : largeur (en mm)
h : épaisseur (en mm)
θ : angle de rotation du ressort (en rad)
l : longueur développée du ressort (en mm)
E : module d'élasticité longitudinal ou d'Young (en Mpa
O
Rotor 2
Stator 1
i
f
r
x
i C M
m
O(1/2)
r
=
2/1
B
B
1
A
h
b
x
y
(
)
k . k B M
a
2/1A
r
θ =
α
Crémaillère 2
2/1
A
A
Pignon 1
d
O
Sens de translation
de la crémaillère
Sens de rotation du
pignon