Les gaz parfaits quantiques II

Physique statistique (PHY433)
Amphi 6
Les gaz parfaits quantiques II
Gilles Montambaux
6 mars 2017 1
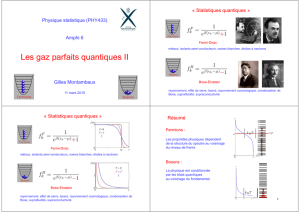
« Statistiques quantiques »
Fermi-Dirac
Bose-Einstein
métaux, isolants, semi-conducteurs, naines blanches, étoiles à neutrons
rayonnement, effet de serre, lasers, rayonnement cosmologique, condensation de
Bose, suprafluidité, supraconductivité
« Statistiques quantiques »
Fermi-Dirac
Bose-Einstein
métaux, isolants, semi-conducteurs, naines blanches, étoiles à neutrons
rayonnement, effet de serre, lasers, rayonnement cosmologique, condensation de
Bose, suprafluidité, supraconductivité
μ(T=0)=²
F
μ≤0
k
B
T
kBT
Fermions :
Les propriétés physiques dépendent
de la structure du spectre au voisinage
du niveau de Fermi
Bosons :
La physique est conditionnée
par les états quantiques
au voisinage du fondamental
Résumé
4

Les Fermions ont tendance à s’éviter : principe d’exclusion de Pauli
Les Bosons ont tendance à se condenser dans le même état
Équation d’état d’un gaz parfait de Fermions / de Bosons
F
B
?
?
5
Les Fermions ont tendance à s’éviter : principe d’exclusion de Pauli
Les Bosons ont tendance à se condenser dans le même état
F
B
A T=0K, les Fermions ont une énergie cinétique finie
les Bosons sont tous dans l’état fondamental
N’oubliez pas
les QCM !
6
Équation d’état d’un gaz parfait de Fermions / de Bosons
Le contrôle…
Le contrôle (3 h) aura lieu le lundi 27 mars de 14h à 17 h
Aucun document autorisé.
Tablette, ordinateur et téléphone interdits.
Calculatrice recommandée.
Un formulaire sera joint au problème.
Dictionnaire papier autorisé pour les EV2 et EV3 densité
Gaz classique
Gaz quantique
Température caractéristique
longueur thermique de de Broglie

I. Généralités: grand potentiel (pression), énergie interne,
facteur d’occupation, densité d’états,
corrections par rapport au G.P. classique
II. Fermions
Propriétés basse température
Deux exemples le gaz d’électrons
les naines blanches
III. Bosons
La condensation de Bose-Einstein
Trois exemples la suprafluidité
les atomes froids
la supraconductivité
Amphi 6
F
B
9
* Le principe de Pauli * impose des conditions sur la nature des états quantiques
* conditionne la répartition des niveaux d’énergie
* et donc la thermodynamique
Fermions Bosons
nombre d’occupation de l’état 10
α=βμ =μ
kT
Résumé : Statistiques quantiques
Fermi-Dirac
AF,B =±kT X
k
ln(1∓fk
)
f
F
k
=1
e
β(²
k
−μ)
+1
fB
k=1
eβ(²k−μ)−1
U=X
k
f
k
²
k
Bose-Einstein
PV =−A
Fermions
Bosons
N=X
k
f
k
²
k
Pression
Grand potentiel
Energie interne
α=βμ =μ
kT
F
B
?
?
Eliminer équations d’état
α
où le potentiel chimique est déterminé par
Équation d’état du gaz parfait quantique
PV =g(N,T
)
U=f(N,T)
U=X
k
fk²k
N=X
k
fk
PV =∓kT X
k
ln(1∓f
k
)

Comment calculer ces sommes ?
U=X
k
f
k
²
k
N=X
k
f
k
PV =∓k
BTX
k
ln(1∓fk
)
μ(T)
13
U=X
~
k
f~
k²~ k
N=X
~
k
f~
k
Pour un gaz parfait, les états sont les états de translation
Dans un grand système, ces états forment un continuum
Remplacer ces sommes discrètes sur par des intégrales sur l’énergie
PV =∓k
B
TX
~
k
ln(1∓f
~
k
)
μ(T)
Comment calculer ces sommes ?
U=X
~
k
f~
k²~ k
N=X
~
k
f~
k
Pour un gaz parfait, les états sont les états de translation
Dans un grand système, ces états forment un continuum
Remplacer ces sommes discrètes sur par des intégrales sur l’énergie
PV =∓k
B
TX
~
k
ln(1∓f
~
k
)
μ(T)
X
k
ϕ(²
k
)=ZD(²)ϕ(²)d²
Comment calculer ces sommes ?
X
k
ϕ(²
k
)=ZD(²)ϕ(²)d²
La densité d’états D( )compte le nombre d’états à une énergie donnée .
Il peut s’agir des états propres d’une particule quantique ou des modes
électromagnétiques ou acoustiques (à une fréquence donnée ) dans une boîte.
D(²)=X
k
δ(²−²
k
)
²
(
D(²)=dN
<
(²)
d²
N
<
(²)=X
k
Θ(²−²
k
)
[
², ² +d²
]
d²
= nombre d’états dans une tranche d’énergie
= nombre d’états d’énergie inférieure à
D(²)d²
N
<
(²
)
On définit aussi
²
( s’appelle aussi densité d’états intégrée )
N
<
(²
)
0
Θ
x
Densité d’états

car dans une boîte de taille , les états sont quantifiés et distants de
L
~
k
2π
L
Dans la limite du continuum,
N
<
(²)=X
~
k
Θ(²−²
~
k
)
N
<
(²)=µL
2π¶
3
Z
²(~ k)<²
d
3
~
k
N
<
(²)=VVolume de l’espace des ~
k|²
~
k
<²
(2π)
3
²(~ k)=²(|~ k|)
N
<(²)=V
(2π)3
4πk3
3
Si , ce volume est isotrope, sphère de rayon
Particule dans une boîte
k(²)
N
<
(²)=V
h
3
4πp
3
3
~p =¯h~ k
remarque
N
<
(²)=µL
2π¶
3
Z
²(~ k)<²
d
3
~
k
c.a.l. périodiques
k
i
=n
i
2π
L
Le résultat ne dépend pas des c.a.l.
n
i
∈Z
k
x
k
y
2π
L
eik
ixi
=eik
i(xi+L)
eik
iL
=1
Densité d’états
Rappel : conditions aux limites
c.a.l. bord dur
k=n2π
L
k=nπ
L
n∈N
∗
c.a.l. périodiques
sin kL =0
n∈Z
²=¯h2k2
2m
²
²
kk
eikx =eik(x+L)⇒eikL =1
×2
×2
×2
×2
×2
×2
×2
La densité d’états ne dépend pas des conditions aux limites 19
²(~ k)=²(k
)
²(~ k)=¯h
2
k
2
2m
N
<
(²)=(2s+1) V
(2π)
3
4π
3µ2m²
¯h
2
¶
3/2
Pour des particules massives,
D(²)=(2s+1) V
4π
2
(2m)
3/2
¯h
3
√²
N
<
(²)=V
(2π)
d
A
d
k
d
N
<(²)∝²d/2
D(²)∝²d/2−1
Si
de spin s
en dimension d
en dimension d=3
N
<
(²)=V
(2π)
3
4πk
3
(²)
3
20