Cours diffraction

DIFFRACTION A L'INFINI PAR UNE OUVERTURE PLANE
Introduction
* historique
Découverte des phénomènes au XVIIe siècle par Grimaldi
Phénomènes étudiés par Huygens (hollandais, 1629-1695)
Interprétation au XIXe siècle par Fresnel (1788-1857)
* diffraction d'autres ondes que les ondes lumineuses
Diffraction d'ondes acoustiques, ondes à la surface de l'eau
* restrictions de l'étude
On fait l'étude seulement de la diffraction à l'infini d'une onde plane, ce qui n'est pas si restrictif car
ce type de diffraction joue un rôle crucial dans la formation des images.
Diaphragme dont on étudie en détail la diffraction : fente rectangulaire (circulaire hors
programme)
I- IDÉES GÉNÉRALES
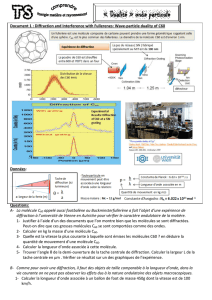
1- Expérience de mise en évidence
dispositif expérimental figure de diffraction
2- Critère de validité de l'optique géométrique :
Si NF<<1 domaine de validité de l'optique géométrique
Si NF>>1 il faut tenir compte de la diffraction
avec où a : ouverture du diaphragme
λ : longueur d'onde de la lumière incidente sur le diaphragme
d : distance diaphragme-écran
II- PRINCIPE D''HUYGENS-FRESNEL ET APPLICATION
1- Présentation
Contribution de Huygens :
analogie ondes à la surface de l'eau/ondes lumineuses
Contribution de Fresnel : utilisation
de la théorie de la théorie ondulatoire
de la lumière et des interférences
lumineuses

2- Réalisation des conditions de diffraction de Fraunhofer
( x , y )
0 0
[ L ]
1
[ L ]
2
d
k
i
k
F
Xx
yz
OF '
P
M
HH '
E c l a i r a g e P l a n d e l a
P u p i l l e O b s e r v a t i o n
ff '
S
Y
3- Formulation mathématique du principe d'Huygens-Fresnel
III- DIFFRACTION A L'INFINI PAR UN DIAPHRAGME PLAN
1- Ouverture rectangulaire
a- Amplitude diffractée b- Éclairement
c- Interprétation de la figure de diffraction
Éclairement en trois dimensions de l'onde diffractée par une ouverture rectangulaire
(pic principal tronqué)

CONCLUSIONS FONDAMENTALES :
avec et
•maxima et minima
maximum principal : il correspond à U = V=0 soit et :
les phénomènes de diffraction modulent les résultats de l'optique géométrique.
Les maxima secondaires se situent à peu près au milieu entre deux minima.
•luminosité de la tache principale
La tache principale reçoit 84% du flux lumineux principal : les maxima secondaires
sont beaucoup moins lumineux que le maximum principal.
•largeur des taches de diffraction
tache centrale : soit et
taches secondaires : et et
donc la tache principale est deux fois plus large que les taches secondaires
Effet de la variation des dimensions de l'ouverture rectangulaire (melusine.eu.org)
diffraction par un trou rectangulaire, de hauteur
5 fois plus grande que la largeur.
diffraction par un trou carré
2- Fente : utiliser la méthode précédente ou calcul direct
3- Ouverture circulaire
figure de diffraction (jf-noblet.fr) : interprétation avec l'intensité 3D (melusine.eu.org)
tache d'Airy
lien rayon de l'ouverture circulaire/ rayon de
la tache centrale de diffraction :
avec r rayon du premier anneau noir : rayon de la tache centrale de diffraction
D diamètre de l'ouverture circulaire
f' distance focale de la lentille L2 ramenant les rayons à l'infini dans son plan focal image.

IV- DIFFRACTION ET POUVOIR DE RÉSOLUTION DES INSTRUMENTS D'OPTIQUE
(HORS PROGRAMME)
1- Position du problème
Par un instrument d'optique, microscope ou lunette astronomique,
l'image d'un point n'est pas un point mais une tache d'Airy. Ceci
empêche l'observateur de distinguer deux objets si les taches
empiètent l'une sur l'autre. On dit que l'instrument ne peut pas
séparer ou résoudre les taches, il a une mauvaise résolution.
Fig a : une étoile Fig a : deux étoiles résolues Fig c : deux étoile à la limite de résolution
2- Limite de résolution d'une lunette astronomique
On souhaite déterminer la valeur minimale de la distance angulaire entre les deux composantes
d'une étoile double pour laquelle on peut séparer les deux taches de diffraction.
Les deux étoiles constituent des sources incohérentes dont on peut superposer les éclairements.
L'oculaire ne limite pas la résolution. L'objectif, qui ramène les rayons dans son plan focal image,
constitue une pupille diffractante circulaire de diamètre D. Pour chaque étoile, il donne une tache
d'Airy.
La règle fixant la limite de résolution est le critère de Rayleigh selon lequel le maximum
principal de la tache de diffraction d'une étoile correspond au premier minimum de la
seconde.
Montrer que la distance angulaire limite vaut
3- Limite de résolution d'un microscope cf. exercice