DS du 13 décembre 2010 : Sujet et corrigé

DS du 13 décembre 2010 : Sujet et corrigé
Exercice 1:
f est une fonction dont le tableau de variation est le suivant :
x-3 -2 0 1 4
fx
-2
0
-1
1
0,5
Pour chacune des affirmations suivantes, répondez par vrai, faux, ou "on ne peut pas savoir", en justifiant
votre réponse.
a)
f−2,5f−2
b)
fx≥−2
pour tout x de
[−3;4]
c)
f1,5f3
d)
f−2,5f0,5
e)
f−2,5f3
a)
f−2,5f−2:
... ... ... ... ... ... ... ... VRAI, en effet la fonction f est strictement croissante sur
[−3;−2],
donc aussi sur
[−2,5 ;−2].
b)
fx≥−2
pour tout x de
[−3;4]:
... VRAI, en effet -2 est le minimum de f sur
[−3;4],
il est atteint
pour
x=−3.
c)
f1,5f3:
... ... ... ... ... ... ... ... ... ... FAUX, en effet la fonction f est décroissante sur
[1;4],
donc
aussi sur
[1,5 ;3]
et on a donc :
f1,5f3.
d)
f−2,5f0,5:
... ... ... ... ... ... ... ... On ne peut pas savoir, en effet d'après le tableau de variations,
on peut seulement déduire que d'une part :
−2f−2,50
et que d'autre part :
−1f0,51
e)
f−2,5f3:
... ... ... ... ... ... ... ... ... VRAI, en effet on remarque que :
f−2,500,5f3
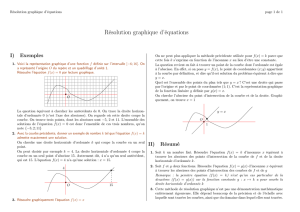
Exercice 2 :
Soit f la fonction définie sur
ℝ
par :
fx=9−x22.
On note
Cf
sa représentation graphique dans le
plan.
1) Développer et réduire
fx,
puis factoriser f(x).
2) Représenter graphiquement f sur votre calculatrice.
3) Lire graphiquement les coordonnées du point d'intersection de
Cf
avec l'axe des ordonnées, puis les
retrouver par le calcul.
4) Lire graphiquement les coordonnées des points d'intersection de
Cf
avec l'axe des abscisses puis les
retrouver par le calcul.
5) Justifier que tous les points de
Cf
ont une ordonnée inférieure ou égale à 9.
Bonus :
6) Justifier que tous les points de
Cf
situés en dessous de l'axe des abscisses ont une abscisse supérieure
à 1 ou inférieure à -5.
1) Forme développée et réduite de f :
Pour tout réel x on a les égalités suivantes :
fx=9−x22=9−x24x4=−x2−4x5
Forme factorisée de f :
Pour tout réel x :
fx=9−x22=32−x22=3−x−23x2=−x1 x5
2) Représentation de f sur la calculatrice : (Il ne fallait rien marquer sur la copie... !!)
3) Intersection de Cf avec l'axe des ordonnées :

En utilisant par exemple la fonction trace du solveur
graphique (touche G-solve) on obtient le graphique de
droite, on en déduit que l'intersection de
Cf
avec l'axe
des ordonnées est le point de coordonnées (0 ; 5)
Pour retrouver ce résultat par le calcul, il suffit de calculer
f0,
et en prenant la forme développée et réduite
de la question 1), le résultat est immédiat.
4) Intersection de C f avec l'axe des abscisses :
En utilisant la fonction ROOT du menu G-solve on obtient
les affichages ci contre. On en déduit que les points
d'intersection de Cf ont pour coordonnées : (-5 ; 0) d'une
part et (1 ; 0) d'autre part.
Retrouver le résultat par le calcul signifie résoudre l'équation
fx=0.
Pour cela, on utilise la forme
factorisée de f obtenue à la question 1).
On a alors l'équivalence :
fx=0⇔ −x1x5=0
D'après la règle du produit nul on a donc :
Soit
−x1=0⇔x=1
soit
x5=0⇔x=−5
Les points d'intersection de
Cf
avec l'axe des abscisses ont donc bien pour coordonnées (-5 ; 0) et (1 ; 0) .
5) Montrons que tous le points de C f ont une ordonnée inférieur ou égale à 9 :
Pour cela on compare
fx
et 9. Une méthode consiste alors à calculer
fx−9
et à montrer que cette
quantité est négative.
Or en prenant la forme de départ donnée pour f(x), il vient :
fx−9=9−x22−9=−x22.
Un carré étant un nombre positif, on a bien que pour tout réel x,
fx−9≤0,
c'est à dire que
fx≤9.
Bonus : 6) Déterminons les abscisses des points de C f situés en dessous de l'axe des abscisses :
Cela revient à résoudre l'inéquation
fx0.
On choisit alors la forme factorisée de f, on se ramène donc à résoudre :
−x1 x50.
Or d'une part :
−x1=0⇔x=1
et d'autre part :
x5=0⇔x=−5
En utilisant alors le sens de variation des fonctions affine (strictement croissante si le coefficient directeur est
positif et strictement décroissante si le coefficient directeur est négatif), on obtient le tableau :
x
−∞
-5 1
∞
−x1
+ + 0 -
x5
- 0 + +
fx
- 0 + 0 -
La courbe de f est donc située en dessous de l'axe des abscisses pour
x−5
ou pour
x1.
Exercice 3 :
On considère la fonction f définie sur I = [-2 ; 4] dont la
représentation graphique Cf dans un repère orthogonal est
donnée ci-contre. Le graphique est à compléter au fur et à
mesure des questions.
On donne le tableau de valeurs ci-dessous :
x-2 -1,83 -1,64 -1 0 1 2 3 3,64 3,83 4
f(x) 16 7 0 -9 0 7 0 -9 0 7 16
1) Donner les images de -2 ; 0 ; 2 et 4 par f.
2) Donner le(s) antécédents(s) de -9 puis de 7 par f.
3) Dresser le tableau de variations de la fonction f sur I.
4) La fonction f admet-elle, sur I, un minimum ou/et un maximum? Pour quelles valeurs sont-ils atteints ?
5) Comment choisir le réel m pour que l'équation f(x) = m admette 4 solutions.

6) Donner le signe de f(x) en fonction des valeurs de x.
7) Résoudre graphiquement :
fx=0
puis
−9fx7.
8) Construire la représentation graphique de la fonction g définie sur I par
gx=2x1.
9) Résoudre graphiquement
fxgx.
1) Images de (-2) ; 0 ; 2 et 4 par f :
D'après le tableau de valeurs, les images de (-2) ; 0 ; 2 et 4 sont respectivement : 16 ; 0 ; 0 et 16
2) Antécédents de (-9) et de 7 :
D'après la représentation graphique de f : - les antécédents de (-9) sont -1 et 3.
- 7 a trois antécédents dont on peut lire les valeurs dans le
tableau : -1,83 ; 1 et 3,83
3) Tableau de variations de f : x -2 -1 1 3 4
f16
-9
7
-9
16
4) Extremum de f sur I :
D'après le tableau ci-dessus : - le maximum de f sur I est 16, il est atteint pour x = -2 et pour x = 4.
- le minimum de f sur I est -9, il est atteint pour x = -1 et pour x = 3.
5) Valeurs de m pour que l'équation f ( x ) = m admette quatre solutions :
L'équation f(x) = m a quatre solution lorsque la courbe
Cf
coupe exactement quatre fois la droite d'équation
y = m, c'est à dire pour m appartenant à l'intervalle ] -9 ; 7 [.
6) Signe de f ( x ) :
Déterminer le signe de f revient graphiquement à trouver les points de
Cf
situés :
- au dessus de l'axe des abscisses
fx0
- en dessous de l'axe des abscisses
fx0
- à l'intersection avec l'axe des abscisses
fx=0
On trouve alors (en comparant la courbe et le tableau de valeurs de f) :
fx0
pour
x∈[−2;−1,64[∪]0;2[∪]3,64 ;4]
fx=0
pour
x∈
{
−1,64 ;0;2;3,64
}
fx0
pour
x∈]−1,64 ;0[∪]2;3,64[
7) Résolution graphique de f ( x ) = 0 :
D'après la question précédente,
fx=0
pour
x∈
{
−1,64 ;0;2;3,64
}
Résolution graphique de -9 < f ( x ) < 7 :
On cherche les point de
Cf
ayant une ordonnée strictement comprise entre -9 et 7. Les solutions sont les
abscisses de ces points.
Par lecture graphique, et en utilisant le tableau de valeurs on trouve que :
S=]−1,83 ;−1[∪]−1;1[∪]1;3[∪]3;3,83[
8) Construction de la représentation graphique de la fonction g :
La fonction g est une fonction affine,
sa représentation graphique est donc une dro ite .
Comme
gx=2x1,
l'ordonnée à l'origine est 1,
la représentation graphique de g passe donc par le point de
coordonnées (0 ; 1).
De plus
g4=2×41=9,
l a représentation graphique de g
passe donc aussi par le point de coordonnées (4 ; 9).
On obtient donc le graphique ci contre :

9) Résolution graphique de f ( x ) > g ( x ) :
On cherche les point de
Cf
situés strictement au dessus des point de
Cg.
Les solutions sont les abscisses
de ces points. Graphiquement on trouve :
S=[−2;−1,6[∪]0,1 ;1,6[∪]3,9 ;4].
Exercice 4 :
Dans une station balnéaire, trois sociétés de location de voitures proposent aux touristes les tarifs suivants :
- Société
S1
: un forfait de 23€ et 0,40€ par kilomètre parcouru.
- Société
S2
: un forfait de 66€, les 72 premiers kilomètres gratuits et 0,30€ par kilomètre au-delà de 70 km.
- Société
S3
: 0,60€ par kilomètre parcouru.
1) Pour une personne qui aura parcouru x kilomètres, calculer :
a) le prix
f1x
qu'elle devra acquitter à la société
S1
b) le prix
f2x
qu'elle devra acquitter à la société
S2
(distinguer les cas (
x≤70
et
x70
)
c) le prix
f3x
qu'elle devra acquitter à la société
S3
2) a) Dans un repère orthogonal (unités : en abscisse 1 cm pour 20km, en ordonnée 1 cm pour 5 €), construire
les représentations graphiques de
f1,f 2
et
f3.
b) Déterminer graphiquement, puis par le calcul, le tarif le plus avantageux selon le nombre de kilomètres
parcourus.
1) Calcul de f 1( x ) :
La société S1 propose une formule avec un forfait de 23€ et 0,40€ le kilomètre parcouru, le coût pour une
personne parcourant x km est donc :
f1x=0,4 x23.
Calcul de f 2( x ) :
La société S2 propose une formule avec un forfait de 66€, 70 km gratuit et 0,30€ le kilomètre parcouru au-delà
de 70km.
- Le coût pour une personne parcourant x km , avec
x≤70
est donc :
f2x=66
- Si
x70
la fonction
f2
est affine de coefficient directeur 0,3. Donc
f2x
est de la forme :
f2x=0,3 xp.
(1)
De plus sa représentation graphique passe par le point de coordonnées (70 ; 66), donc
f270=66.
Or, d'après (1),
f270=0,3×70p=21p
Donc :
21p=66 et donc p=66−21=45
Finalement, si
x70,
f2x=0,3 x45.
Calcul de f 3( x ) :
La société S3 propose une formule à 0,60€ le kilomètre parcouru. Le coût pour une personne parcourant x km
est donc :
f3x=0,6 x.
2 a) Voir sur la page ci-après.
b) Détermination du tarif le plus avantageux selon le nombre de kilomètre parcouru :
1] En utilisant le graphique :
On cherche quelle est la courbe de tarif située sous les deux autres pour une abscisse donnée.
Par lecture graphique, on trouve que :
- Si
x≤115,
le tarif le plus avantageux est celui de la société S3.
- Si
115x≤220,
le tarif le plus avantageux est celui de la société S1.
- Si
x220,
le tarif le plus avantageux est celui de la société S2.
2] Par le calcul :
Comparaison de
f1
et de
f2
sur [0 ; 70] :
f170=0,4×7023=51
donc
f17066
Or la fonction
f1
est strictement croissante (son coefficient directeur est strictement positif),
Donc
f1
est strictement inférieure à
f2
sur [0 ; 70].
On montre de même que
f3
est strictement inférieure à
f2
sur [0 ; 70].

•Comparaison de
f1
et de
f2
si x > 70 :
Pour comparer ces deux fonctions on peut étudier le signe de leur différence
g1−2
:
Si
x70, g1−2x=f2x−f1x=0,3 x45−0,4 x23=−0,1 x22
donc :
g1−2x=0⇔x=−22
−0,1 =220
On a donc le tableau de signes :
x
−∞
220
∞
g1−2x
+ 0 -
Donc si
70x220, g1−2x0,
c'est à dire que
f1xf2x.
Avec ce qui a été démontré plus haut, on en déduit que la société
S1
propose un tarif plus avantageux que
celui de la société
S2
pour une distance parcourue comprise entre 0 et 220 km. Au delà, le tarif de la
société
S2
devient plus intéressant.
•On compare donc maintenant les tarifs de la société
S1
et de la société
S3
:
On étudie donc le signe de la fonction
g1−3
définie par
g1−3x=f3x−f1x:
Expression de
g1−3x
:
g1−3x=0,6 x−0,4 x23=0,2 x−23
donc :
g1−3x=0⇔x=23
0,2=115
On a donc le tableau de signes :
x
−∞
115
∞
g1−3x
- 0 +
Donc si
0x115, g1−3x0,
c'est à dire que
f3xf1x.
La société
S3,
est donc plus intéressante que la société
S1
pour une distance parcourue comprise entre
0 et 115 km. Au delà, la société
S1
est plus intéressante que la société
S3.
Conclusion : Si la distance parcourue est inférieure à 115km, le tarif le plus avantageux est celui de la
société
S3.
Si la distance parcourue est comprise entre 115km et 220km, le tarif le plus avantageux est
celui de la société
S1.
Au delà de 220km, le meilleur tarif est celui de la société
S2.