Les ondes mécaniques progressives périodiques

Les ondes mécaniques progressives périodiques
I.Observation de mouvements périodiques par stroboscopie
I.a. Les mouvements périodiques



Un mouvement qui se répète à intervalles de temps égaux, de manière identique, est
dit périodique.
La période T est le mis pour que le système se retrouve dans le même état
consécutivement
La fréquence F (en hertz Hz) est l’inverse de la période T (en seconde s).
F= 1
T
Exemples : balançoire, pendule, ressort, marée, rotation de la Terre
I.b. La persistance rétinienne
Expérience de la diode :
L’oeil ne peut pas détecter des mouvements qui ne durent pas plus de 0,1 seconde.
I.c. Introduction à la stroboscopie
La stroboscopie donne l’impression qu’un mouvement périodique est immobilisé ou ralenti
dans le temps
II.Ondes progressives périodiques à une dimension
Définition
Une onde progressive périodique est générée par un une source qui impose une perturbation
périodique.
III.Onde progressive sinusoïdale à une dimension
III.a. Définition. Périodicité temporelle T
Vous vous baignez dans la mer il y a des vagues vous ne bougez pas.
 Représenter le niveau de l’eau en fonction du temps
 Indiquer la période T
 Exprimer la fréquence F en fonction de T
TS
Page 1
10
Niveau de
l’eau
9
8
7
Période T
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18
Temps
III.b. Périodicité spatiale : longueur d’onde λ
Le temps s’est arrêté, vous êtes toujours dans l’eau.
 Représenter le niveau de l’eau en fonction de la position x quand on se déplace sur la
mer pour un instant donné.
 Indiquer la longueur d’onde λ.
10
Niveau de
l’eau
9
Longueur
d’onde λ
8
7
6
5
4
3
2
1
0
0
TS
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18
Position x
Page 2
III.c. Relation entre la période T et la longueur d’onde λ.
Animation
Niveau de
l’eau
10
La longueur d’onde λ est la distance
parcourue par l’onde durant la période
T à la vitesse V (V est la célérité de
l’onde).
On peut donc écrire :
9
8
7
λ
𝛌= 𝐕×𝐓
6
5
4
3
2
𝑡1
1
𝑡3
𝑡2
Position x
0
0
2
4
6
8
10
12
14
16
18
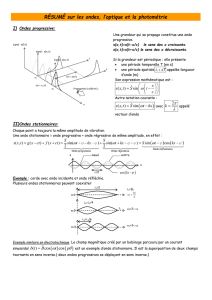
III.d. Etude mathématique (hors programme)
Y
M
Célérité C de l’onde
YM
A
O
xM
x
Animation 1
Animation 2
Une onde peut-être modélisée par un cosinus ou un sinus :
 A : amplitude
TS
Page 3
 T : période
 t : temps (ici variable)




2 .t
)
T
M reproduit le mouvement de O avec un retard τ (l’onde est passée en O puis en M)
x
τ= M
C
2 .(t   )
En xM on écrire que l’élongation vaut Y(t,xM) = A sin(
)
T
2 .t 2 .xM
soit Y(t,xM) = A sin(
)
T C
T
2 .t 2 .xM
De plus λ = T.C d’où : Y(t,xM) = A sin(
)

T
Pour simplifier l’écriture on introduit 2 autres grandeurs :
2.
 ω=
= 2π.F en rad.s-1
T
2.
 k=
en rad.m-1
En x0 =0 on peut écrire :
Y(t,x0) = A sin (

Périodicité temporelle
Périodicité spatiale
Y(t, xM) = A sin(ω.t – k.xM )
Cette équation modélise une onde progressive périodique d’amplitude A qui se
propage vers les x positifs
IV.Cas de milieux à deux ou trois dimensions
IV.a. Ondes circulaires à la surface de l’eau : deux dimensions
TS
Page 4
Animation
IV.b. Cas du son : trois dimensions
Animation sonores.gif
Extrait CPS : le son
1) Quel est le domaine de fréquences audible pour l’homme ?
20 hz - 20 000 Hz
2) Est-ce que le son se propage dans le vide ?
Non, car il faut un support matériel
3) Est-ce que la vitesse du son est la même dans tous les matériaux
La vitesse du son dépend des matériaux traversés, plus il est dense plus la vitesse du
son est grande
V.Diffraction des ondes progressives sinusoïdales
V.a. Phénomène de diffraction
Représenter l’onde après le trou.
θ
Trouver l’illustration de diffaction
TS
Page 5
Voir complément
Ici représentation de la fonction :
𝜋 𝑎 sin 𝜃 2
𝑠𝑖𝑛 (
)
𝜆
𝐼 = 𝐴2 (
)
𝜋 a sin 𝜃
𝜆
2
a
Intensité I

a

a
Sin θ
2
a
V.b. Influence des dimensions de l’ouverture ou de l’obstacle
diffractant
𝐎𝐧 𝐚𝐮𝐫𝐚 𝐥𝐚 𝐩𝐫𝐞𝐦𝐢è𝐫𝐞 𝐞𝐱𝐭𝐢𝐧𝐜𝐭𝐢𝐨𝐧 𝐩𝐨𝐮𝐫
𝝀
𝐬𝐢𝐧 𝜽 =
𝒂
 a < λ alors 1 <
 a = λ donc
 a > λ alors

il n’y pas de direction ou l’amplitude de l’onde est nulle
a

= 1. La tache centrale est très grosse les minimums sont aux extrémités
a

2
<1,
< 1 … donc il existe une ou plusieurs directions où
a
a

l’amplitude de l’onde est nulle. A chaque fois que sin θ = k
TS
a
où k = 1, 2,3 …
Page 6
amplitude de l'onde
a<λ
a≈λ
-1
a>λ
1
Sin θ
Tout phénomène physique pour lequel on observerait un phénomène de diffraction peut-être
considéré comme ondulatoire.
VI.Milieu dispersif
Si la célérité d’une onde dans un milieu donné dépend de la fréquence alors le milieu est dit
dispersif.
D’après le document ci-contre, est-ce que la
surface de l’eau est un milieu dispersif pour
les vagues ?
On voit que les ondes basses fréquences se
propagent moins vites que les ondes de
hautes fréquences, donc la surface de l’eau
est un milieu dispersif pour les vagues.
Est-ce que l’air est un milieu dispersif pour le
son ?
Non l’air n’est pas vraiment un milieu
dispersif pour le son.
TS
Page 7
7,9,22,25 P 43
TS
Page 8