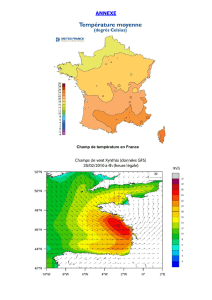
Physique Appliquée à la Géologie (Cours) STU — S3

Université Sidi Mohamed ben Abdellah
Faculté des Sciences Dhar El Mehraz — Fès
Département de Géologie
Physique Appliquée à la Géologie
(Cours)
STU — S3
Pr. Abdelkrim AHARMOUCH
Année Universitaire : 2016—2017

1
Chapitre 1
LA BOITE A OUTILS
1. Fonctions à valeurs scalaires
1.1. Fonctions de points à valeurs scalaires
On peut étendre la notion de fonction au cas où la connaissance des valeurs de nvariables est
nécessaire.
3
( , , ) ( , , )x y z f x y z .
La fonction fétant à valeurs scalaires.
On définit 2 types de scalaires :
– un vrai scalaire , dont le signe est indépendant du référentiel. Par exemple : la masse,
la pression la température le potentiel électrique,…etc.
– un pseudo scalaire mais dont le signe dépend du référentiel. Par exemple le moment
d’une force.
En physique il existe des fonctions à valeurs scalaires qui sont définies en tout point de
l’espace : ( , , ) ( , , )M u v w f u v w . Ce sont des fonctions de point. On les note :
( , , ) ; ( ) ou ( )
f u v w f M f OM
Exemples :
La pression P, la température T, le potentiel électrique V, …etc.
Si on définit dans une région de l’espace une fonction de points à valeurs scalaires, on dit
qu’on a un champ de scalaire.
Pour le caractériser, on prend ( )
f M Cte
et on définit une surface de niveau ou (une
surface équipotentielle).
Exemple :
L'espace
M , O un point fixe (l’origine). La position de M para rapport à O est définie
par :
OM r
. On cherche l’équipotentielle correspondant à la fonction scalaire définie par :
2
( )f M
r
.
Pour cela on résout l’équation : 2 ( )
f M Cte
r
  .
On trouve :
(constante)
r C . C’est l’équation d’une sphère. L’équipotentielle est donc une
sphère de rayon r.
1.2. Différentielles et Dérivées
Soit f une fonction réelle d’une variable réelle :

2
:( ) f
x f x y
On dit que fest différentiable au point x0s’il existe une application linéaire
h lh
et une
fonction
( )
h h
définie sur un intervalle I de centre zéro telles que :
0 0
0
( I) ( ) ( ) ( )
avec
lim 0.
h
h f x h f x lh h h
(1)
L’application :
h lh
est appelée fonction linéaire tangente à la fonction fau point x0. On la
note
0
x
df
.Le nombre ls’appelle le coefficient de la différentielle de fau point x0.Nous avons
donc pour tout hréel :
0( )
x
df h lh
(2)
Il résulte de la définition qu’une fonction f différentiable en x0est définie sur un intervalle
ouvert centré sur x0et vérifiant (1) :
0 0
0
( ) ( )
( ) lim 0.
h
f x h f x l h h avec
h
(3)
Donc :
0 0
0
( ) ( )
lim
h
f x h f x
l
h
(4)
Réciproquement si 0 0
0
( ) ( )
lim
h
f x h f x
l
h
on peut trouver une fonction telle que :
0 0
( ) ( )
( ) f x h f x
h l
h
sur un intervalle I de centre 0 (exclu) et telle que
(0) 0
.
Nous avons alors :
0 0
( I) ( ) ( ) ( )
h f x h f x lh h h
      (5)
étant définie sir I et telle que 0
lim 0
h
Nous voyons donc que la recherche de la fonction linéaire tangente à fen x0(
h lh
) revient
à la recherche de la limite :
0 0
0
( ) ( )
lim
h
f x h f x
h
(6)
Dire que fest différentiable en x0équivaut à dire que 0 0
0
( ) ( )
lim
h
f x h f x
l
h
. Cette limite
est le coefficient de la différentielle en x0. C’est aussi est aussi la dérivée de fau point x0et on
dit que fest dérivable en x0.On note 0
( )
f x l
.
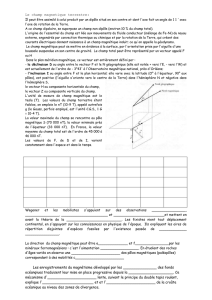
Interprétation géométrique de la dérivée et de la différentielle.

3
Figure 1. Dérivée et différentielle.
L’équation de la tangente
0
en
0
x
est donnée par :
0 0
( ) ( )
y f x l x x
   (7)
De (1) on peut voir que si
0
l
,
lh
est une valeur approchée de
0 0
( ) ( )
f x h f x
  pour
h
"petit", soit géométriquement (Figure 1) :
'
PM PM
(8)
'
PM lh
est la valeur de la différentielle de fau point x0pour un accroissement hde la
variable x.
Le calcul de la différentielle est utile aux calculs d’incertitudes. En effet on peut apprécier
l’erreur commise sur une quantité physique
( )
f x
dès lors que l’on connait l’erreur commise
sur la variable xdont elle dépend suivant la loi :
( ) ( )
df x f x dx
.
Exemple :
Calcul de l’erreur sur l’énergie cinétique :
2
1
2
E mv
dE dE dv
mv
dt dv dt
Donc connaissant l’erreur commise sur la mesure du temps t, on peut connaitre l’erreur
commise sur l’énergie E. Nous obtenons :
E mv t

4
1.3. Différentielles et dérivées de fonctions de plusieurs variables
Comme pour des fonctions à une seule variable, on peut aussi définir des différentielles et des
dérivées de fonctions à plusieurs variables.
Soit
( , , )
f x y z
une fonction et x,y,zde 3 variables indépendantes. On définit la dérivée par
rapport à xpar exemple de la façon suivante :
0 0 0 0 0 0
0
0
( , , ) ( , , )
lim ( )
x
h
f x h y z f x y z
f x
h
(9)
On définira les dérivées par rapport à yet zde la même façon que pour x. Ces dérivées sont
dites des dérivées partielles premières (ou de premier ordre) par rapport à x,yet zet sont
notées respectivement : , ,
f f f
x y z
ou
, ,
x y z
f f f
ou encore , ,
x y z
f f f
.
Exemple :
2
( , ) 2 ln
f x y x y
2
2ln .2
1
2 .
f
y x
x
fx
y y
La différentielle dans le cas d’une fonction de plusieurs variables.
Soit
( , , )
f x y z
une fonction et x,y,zde 3 variables indépendantes. La différentielle est
obtenue de la façon suivante :
f f f
df dx dy dz
x y z
   (10)
Les dérivées d’ordre supérieur :
Pour une seule variable :
2
2
,
x x
df
d
df d f
dx
f f
dx dx dx
   (11)
Pour plusieurs variables :
2 2 2 2
2 2 2
, , ,....., ,....
f f f f
x x y y z      (12)
Remarque
L’ordre des dérivations peut être changé sans que pour autant le résultat change. Nous aurons
alors :