Modelisation et simulation sous matlab/simulink de la

http://www.ucadjds.org Journal des Sciences
S. Ndoye et al / J. Sci.Vol. 9, N° 2 (2009) 45 – 55 - 45 -
MODELISATION ET SIMULATION SOUS MATLAB/SIMULINK DE LA CHAINE
D’ALIMENTATION D’UNE STATION RELAIS DE TELECOMMUNICATIONS EN ENERGIE
SOLAIRE PHOTOVOLTAIQUE DANS UNE ZONE ISOLEE DU RESEAU ELECTRIQUE
Souleymane NDOYE+, Ibrahima LY++, Fabé Idrissa BARRO+, Ould Habiboulahi LEMRABOTT+++,
Grégoire SISSOKO+*
+ Laboratoire de Semiconducteurs et d’Energie Solaire, Département de Physique,
Faculté des Sciences et Techniques, Université Cheikh Anta Diop, Dakar, SENEGAL
++Département Génie Electromécanique, Ecole Polytechnique de Thiès, Sénégal
+++ Ecole Supérieure Multinationale de Télécommunications, Sénégal
Abstract:
Theorical study of the solar cell is based on one diode
representation. The temperature and irradiance effects on the
solar cell are studied, particularly on the short circuit current
Icc, the open circuit voltage Vco, the photovoltaic conversion
efficiency η, and the fill factor FF.
Depending on the load (a base transmitter station BTS, I=60A,
V=48V)) direct current, and the operating conditions
(temperature, irradiance), we can found a highly gap between
the potential peak power and the real power transferred to the
BTS.
A maximum power point tracker (MPPT) based on a boost
converter driven by a Pulse Width Modulation (PWM) is used
for extracting the maximum power from the solar photovoltaic
generator.
The modeling and simulation of the system (photovoltaic
generator, boost converter, Pulse Width Modulation and MPPT
algorithm P&O) is then made with Matlab / Simulink software.
Résumé:
L’Etude théorique de la photopile est basée sur une
représentation à une diode de la photopile. Les effets de la
température, de l’irradiation sur la photopile sont étudiés, en
particulier, sur les grandeurs telles que le courant de court circuit
Icc, la tension de circuit ouvert Vco, le rendement η et le facteur
de forme FF. Selon les caractéristiques de la charge à courant
continu (3kW) , qui est une station relais de télécommunications
BTS (I=60A, V=48V) et les conditions de fonctionnement
(température, Irradiation), nous pouvons trouver un très fort
écart entre la puissance maximale potentielle du générateur et
celle réellement transférée à la BTS. Afin d’extraire à chaque
instant le maximum de puissance disponible aux bornes du GPV
et de la transférer à la BTS, on utilise un étage d’adaptation
composé d’un hacheur Boost commandé par une modulation de
largeur d’impulsion(MLI).
La modélisation puis la simulation du système (générateur
photovoltaïque, hacheur Boost, Modulation de largeur
d’Impulsion de même que l’algorithme MPPT) est ensuite
effectuée grâce au logiciel Matlab/Simulink.
Keywords: Photovoltaic generator, BST, Boost converter, PWM,
MPPT
Mots clés: Générateur photovoltaïque, BTS, Hacheur Boost, MLI,
MPPT.
I. INTRODUCTION
Nous étudions dans cet article le meilleur moyen de transférer toute la puissance utile du générateur
photovoltaïque à une station relais de télécommunications (BTS) [1]. Sachant que sur la caractéristique
courant-tension du générateur (qui dépend des conditions d’éclairement, de température, de vieillissement),
il existe un point de fonctionnement où la puissance débitée est maximale, l’optimisation consiste à se fixer
sur ce point en permanence en agissant de façon automatique sur la charge vue par le générateur. Cette
adaptation de charge s’effectue à l’aide d’un convertisseur statique dont les pertes doivent être aussi faibles
que possible et qui peut, par ailleurs, assurer une fonction de mise en forme d’une grandeur de sortie
(conversion continu-continu avec modification de tension).
Nous avons choisi d’utiliser la technologie de recherche du point de puissance maximale MPPT [2, 3],
basée sur l’algorithme « Perturb and Observ (P&O)» [4], commandé par un signal en Modulation de largeur
d’Impulsion (MLI) [4-6].
Une modélisation sous Matlab/Simulink des différentes parties du système est proposée.
* Auteur correspondant : Email : [email protected]m

http://www.ucadjds.org Journal des Sciences
S. Ndoye et al / J. Sci.Vol. 9, N° 2 (2009) 45 – 55 - 46 -
II. MODELISATION DU SYSTEME
Le système étudié est constitué par le générateur PV, le convertisseur DC-DC (hacheur de type survolteur) et la
BTS, de puissance égale à 3kW. Le convertisseur DC-DC est commandé par un signal à modulation de largeur
d’impulsion avec une stratégie de recherche du point de puissance maximale MPPT.
La figure ci-dessous présente le synoptique de l’ensemble du système :
Figure 1 : Schéma synoptique du système PV contrôlé par
MPPT
La commande MPPT délivre l’action de contrôle appropriée afin de suivre le point de puissance maximale en
chaque instant. Ce contrôle, dans le cas d’un transformateur DC, agit directement sur le rapport cyclique du
convertisseur DC-DC.
II.1 Modèle du module photovoltaïque
Dans le cas idéal, la jonction PN soumise à l’éclairement photovoltaïque connectée à une charge peut être
schématisée par un générateur de courant Icc en parallèle avec une diode. Sous obscurité, l’équation de la
diode est donnée par [7, 8]: = [ exp 
 1] (1)
Sous éclairement, on aura : = [exp 
1] (2)
Avec : Is, courant de saturation inverse de la diode ; q, la charge de l’électron (1.6 10-19C) ; k, la
constante de Boltzmann (1.38 10-23J/K) ; n, le facteur de non idéalité de la photopile (1< n <2) ; T, la
température de la jonction en K ; i, le courant circulant dans la diode ; I, le courant de sortie, et V la tension de
sortie.
En circuit ouvert, la charge tend vers l’infini et V tend vers Vco, qui est la tension en circuit ouvert.
Lorsque les résistances de contacts et les pertes ohmiques sont prises en compte comme dans le cas réel,
nous devons associer au schéma équivalent une résistance série (Rs) et une résistance parallèle (Rp), le
modèle de la cellule devient :
Figure 2 : Modèle d’une cellule réelle
Ainsi l’équation (2) devient :
= exp +
  1  (3) avec = +

http://www.ucadjds.org Journal des Sciences
S. Ndoye et al / J. Sci.Vol. 9, N° 2 (2009) 45 – 55 - 47 -
Dans le cas idéal, on a Rs qui tend vers 0 et Rp qui tend vers l’infini.
Ces résistances (Rs et Rp) donnent dans le cas réel une évaluation des imperfections de la diode ; en
considérant que Rs présente une valeur faible et que Rs<<Rp, les pentes de la caractéristique I(V) sous
illumination, calculées en I=0 (circuit ouvert) et V=0 (court circuit), donnent respectivement les valeurs
inverses des résistances série et shunt.
II.1.1 Influence de la température
L’équation de Boltzmann donne : Is = Io exp (eVo/kT). L’expérience montre que la tension de circuit ouvert
d’une cellule solaire diminue avec l’augmentation de la température de la cellule. Un ordre de grandeur
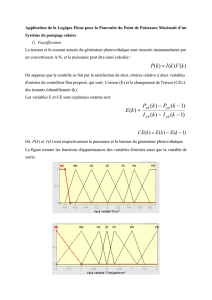
courant de la perte est de 2.3mV/°C/cellule [8]. Nous présentons ci-dessous la caractéristique I-V d’un module
photovoltaïque pour un niveau d’ensoleillement G donné et pour différentes températures :
Figure 3 : Caractéristique courant-tension pour différentes
valeurs de la température
Le courant de court circuit, par contre, augmente légèrement avec la température de la cellule (environ 0.05%
par degré Celsius).
II.1.2 Influence du rayonnement
Nous avons fait varier le niveau d’ensoleillement G et tracé les caractéristiques I-V associées :
Figure 4 : Caractéristique courant-tension pour différentes valeurs
du rayonnement
II.2 Modélisation du générateur photovoltaïque
0 5 10 15 20 25 30 35 40 45 50
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5Courbe I-V du module à G constant pour diverses températures
Tension Module en V
Courant Module en A
0°C
25°C
50°C
75°C
PPM
0 5 10 15 20 25 30 35 40 45 50
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5Courbe I-V du module à T constante pour divers ensoleillements
Tension Module en V
Courant Module en A
1000W/m2
800W/m2
600W/m2
400W/m2
200W/m2

http://www.ucadjds.org Journal des Sciences
S. Ndoye et al / J. Sci.Vol. 9, N° 2 (2009) 45 – 55 - 48 -
La puissance délivrée par une cellule ne suffit par pour alimenter une charge DC de la taille d’une station
relais de télécommunications (BTS). Il va falloir interconnecter plusieurs cellules en série et en parallèle pour
former un module photovoltaïque et atteindre la puissance désirée.
A leur tour, l’interconnexion de modules entre eux en série et en parallèle, pour obtenir une puissance
encore plus grande, définit la notion de générateur photovoltaïque (GPV).
Pour chaque module, le constructeur, le constructeur donne le courant de court-circuit (Icc) et la tension de
circuit couvert (Vco) aux conditions standards (T=25°C et Es=1000W/m2).
Si on pose Ns, le nombre de modules connectés en série dans une branche et Np, le nombre de
branches connectées en parallèle.
Le schéma équivalent du générateur photovoltaïque devient :
Figure 5 : Modèle du générateur
photovoltaïque
L’équation régissant ce modèle de générateur photovoltaïque est obtenue à partir de l’équation (3) :
= exp + 
 1 (4)
Ce qui donne
 exp +
 1=
et : exp( (+ 
)
 ) =   + 1
puis :
+ 
=  ln   + 1
d’où :
= 
ln    + 1  (5)
A partir de l’équation (5), nous établissons le modèle Simulink du générateur photovoltaïque donné par la
figure suivante :
Figure 6: Modèle Simulink du générateur photovoltaïque
II.3 Modélisation du hacheur boost
alpha del I
del V Ns
Np
2
Inew
1
Vnew
25
Tref
Vref
Iref
Subsystem
0.7
Rs Product3
Product2
Product1
Product
11/2
Ns/Np
2.41
Isc
1000
Gref
4
35
-K-
-K-
Beta
1
1
2
G
1
T

http://www.ucadjds.org Journal des Sciences
S. Ndoye et al / J. Sci.Vol. 9, N° 2 (2009) 45 – 55 - 49 -
Le convertisseur continu-continu est un hacheur à transistor de type parallèle donc élévateur de tension.
Il est dimensionné pour une puissance de 3kW correspondant aux valeurs nominales I=60A, V=48V, coté BTS,
et I=172A et V=17.4V, coté générateur. Son rapport de transformation est, en appelant α le rapport cyclique
(rapport du temps pendant lequel le transistor est fermé, à la période de hachage) :
= 1 1 avec α < 1
Pour une puissance incidente, la puissance optimale transférée à la charge ne pourrait être maximale que
pour un rapport cyclique bien défini.
Ce modèle de hacheur Boost ou Hacheur survolteur, est utilisé pour augmenter la tension de sortie, par
rapport à la source. Sa forme la plus simple est présentée comme suit [9]:
Figure 7: Forme simple du hacheur Boost
Ce hacheur comporte trois composants :
Une inductance L, une capacité C et un interrupteur qui peut prendre deux états, u=1 et u=0.
Son principe peut être expliqué de la manière suivante :
Quand l’interrupteur est en position 1, le circuit est séparé en deux parties : à gauche, la source charge
l’inductance, pendant ce temps, la capacité à droite maintient la tension de sortie utilisant l’énergie
précédemment stockée. Quand l’interrupteur change de position vers 0, la source DC et l’énergie stockée
dans l’inductance vont ensemble alimenter le circuit à droite, d’où une augmentation de la tension de sortie.
Dans les conditions idéales, c’est à dire : interrupteur idéal, capacité idéale et inductance idéale, le hacheur
Boost peut être modélisé en utilisant les équations différentielles ordinaires suivantes :
 =1    (6)   =1 (7)
V0 = Ri (8)
Le modèle Simulink du hacheur idéal est alors le suivant :
Figure 8 : Modèle Simulink du hacheur idéal
Dans le cas général, une résistance interne à l’inductance, RL et une résistance interne à la capacité RC,
peuvent être ajoutées au modèle précédent.
Les équations (6) et (7) deviennent :
 =1 0   (9)   =1 (10)
IL
V0
IL
2
V0
1
Vin
5
V0,iL
Subtract
Masse
0
MOSFET 1
MOSFET
Integrator 1
1
s
Integrator
1
s
1/R
1/6
1/L
-K-
1/C
-K-
MLI
1