Lettre au format pdf

Mardi 12 décembre 1995 à 17 h
Analyser un son
Bernard Vuilleumier
On appelle son pur la sensation auditive produite par une oscillation harmonique simple. On
obtient un son doué de timbre en superposant des sons purs de fréquences f, 2f, 3f, ... nf, où f
est la fréquence fondamentale déterminant la «hauteur» du son et 2f, 3f, ... n f les h a r m o n i q u e s
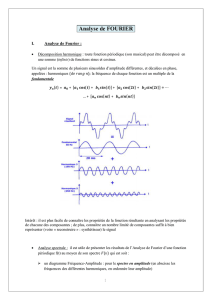
naturels. La forme obtenue en superposant plusieurs sons purs s’appelle enveloppe. Si nous
reportons l’amplitude ades différentes composantes d’un son doué de timbre en fonction de
leurs fréquences f, nous obtenons le spectre du son (fig. 1 c).
Fig. 1. A gauche: Superposition de trois sons purs de fréquences f, 2fet 3f; au centre: enveloppe du son
r é s u l t a n t; à droite: spectre des fréquences.
Nous percevons un son lorsque l’air ambiant ébranle nos tympans. Les sons qui
sont généralement considérés comme plaisants peuvent être décrits à l’aide de fonctions
p é r i o d i q u e s. Considérons les fonctions y= sin(t) et y= sin(4t):
La première oscille une fois en 2πsecondes et la deuxième quatre fois dans le même temps.
Si nous voulons une fonction présentant foscillations par seconde, nous devons donc écrire
y= sin(2πft). Lorsqu’une corde ébranle l’air ambiant en vibrant à la fréquence f, l ’ a m p l i t u d e
de vibration yen un point de la corde peut être décrite à l’aide de la fonction y= sin(2πft).
Le logiciel Mathematica est capable d’enregistrer environ 8000 fois par seconde l’amplitude
d’une telle fonction, de la convertir en une tension et de soumettre un haut parleur à cette
tension. Cette technique, qui permet d’obtenir une suite de nombres à partir d’une fonction,
est appelée échantillonnage. Il est possible, à partir d’une liste de nombres, d’obtenir une
somme de fonctions sinus et cosinus qui définissent une fonction périodique. Cette opération
s’appelle une transformation de Fourier. Lorsque nous enregistrons un son à l’aide d’un
ordinateur, nous effectuons en fait un échantillonnage qui fournit une liste de nombres.
En enregistrant un son d’une durée d’une seconde par exemple, nous obtenons déjà une liste
comportant plusieurs milliers de nombres. Si nous faisons subir une transformation de Fourier à
cette liste, nous obtenons une somme de fonctions sinus et cosinus déraisonnablement l o n g u e .
Mais il est possible de réduire le volume des données: les fonctions dont les coefficients sont
très petits peuvent être ignorées, et si nous considérons plusieurs périodes, il n’est plus
nécessaire de distinguer, pour une fréquence donnée, les termes cosinus des termes sinus car il
s’agit uniquement d’un déphasage qui n’a pas d’importance pour un son d’une certaine durée.
En regroupant les termes restants par fréquences et en présentant le résultat sous la forme de
couples {amplitude, fréquence}, nous obtenons une liste d’une longueur plus raisonnable qui
définit le spectre du son.
odélisation
imulation
Centre informatique
pédagogique (CIP)
Rue Théodore-de-Bèze 2
Case Postale 3144
1211 GENÈVE 3
Tél: [phone]
Fax: [phone]
Directeur: Raymond Morel
Lettre nº 44
Le timbre d’un son est lié à
la présence d’harmoniques,
c’est-à-dire de sons dont les
fréquences de vibration sont
des multiples entiers de la
fréquence fondamentale
Echantillonner un son,
c’est examiner et enregistrer
l’amplitude de la fonction qui
le décrit un grand nombre de
fois par seconde
y y a
t t f
π2π π 2π

Travaux pratiques
Mots clefs
oscillation, son, h a r m o n i q u e, enveloppe, spectre, échantillonnage, transformation de Fourier.
Exercice 1
Supposons qu'une corde de longueur 2ldonne, en vibrant, la note mi. Une corde de longueur
ldonne le m i situé une octave au-dessus. Une corde de longueur égale à la moyenne harmonique
4l/3 de ces deux longueurs donnera le s i, et une corde de longueur égale à la moyenne
a r i t h m é t i q u e 3l/2 le la.
a) Comment la moyenne harmonique divise-t-elle l'octave mi-mi ?
b) Comment la moyenne arithmétique divise-t-elle l'octave mi-mi ?
c) Calculez, en partant des longueurs 2let l, les longueurs de corde donnant les notes si, mi,
la, ré, sol, do, fa en utilisant une moyenne harmonique, puis des moyennes arithmétiques.
N.B. Les longueurs obtenues doivent toujours être comprises entre 2let lpour que les
notes se trouvent dans l'octave de départ. Les notes obtenues par ce procédé forment la
gamme de Pythagore.
d) Calculez le rapport des longueurs de corde – ou intervalles – des notes voisines.
Exercice 2
a ) Dessinez – à la souris, sur l’écran – une centaine de points sur un système d’axes, et formez la
liste des coordonnées de ces points.
b ) Répartissez ces points sur l’intervalle 0 – 2π en les espaçant régulièrement et formez la liste
des ordonnées (échantillon).
c ) Construisez une fonction périodique qui prend les valeurs de l'échantillon.
d ) Calculez les fréquences à partir de l'échantillon, comptez le nombre de composantes et
dessinez le spectre obtenu.
e ) Supprimez toutes les fréquences dont l’amplitude est inférieure à un certain seuil. Comptez le
nombre de composantes et dessinez le nouveau spectre.
f) Reconstruisez les fonctions correspondant à chaque spectre et comparez-les.
P rochaine réunion: mardi 16 janvier 1996 à 17h .
Pour mettre en relation la
consonance des sons et la
longueur des cordes vibrantes
qui les produisent
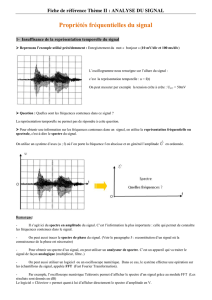
Pour obtenir un spectre de
fréquences à partir d’un
échantillonnage d’amplitudes
à l’aide d’une transformation de
F o u r i e r