l`alternateur synchrone - Le blog de Mesures Physiques

L’ALTERNATEUR SYNCHRONE
I) Définition et intérêt :
1) Définition :
Un alternateur synchrone = machine électrique tournante en mode génératrice et produisant de
l’énergie électrique alternative.
Nous étudierons le cas d’un alternateur synchrone triphasé : l’induit peut être câblé en Y ou en ∆.
2) Intérêt :
 Convertie de la puissance méca. en puissance électrique.
 Principe simple et rendement très important ( 100 %)
 Peut être intégré dans des systèmes embarqués et dans des installations de puissance
 Sa taille est négligeable par rapport à la puissance délivrée
Ex : un alternateur de centrale = plusieurs dizaines de  pour un diamètre de plusieurs dizaines de mètre
 L’alternateur est la base de presque toute la production d’énergie électrique mondiale
II) Principe de fonctionnement :
1) Production d’une f.e.m sinusoïdale dans une bobine :
Avec  : la valeur efficace du champ d’induction magn. tel que : , =.
Et le flux d’induction : =.2. .. sin(.) , Avec S : section de la bobine.
Par suite, comme =
 , on obtient =.2. ...cos()
 =.2. cos() ; Avec =...
Notons qu’une période correspond à une rotation du champ magn. d’un tour.
2) Principe de la production de forces électromotrices triphasées équilibrées :
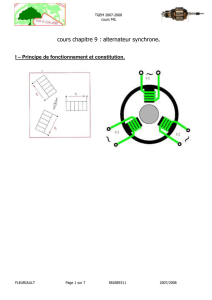
Soit trois bobines identiques décalées entre elles de 120° et soumise au même champ tournant.
A ces décalages correspondent des retards de phase de 2
 et de 4  d’où :
1=.2. cos()
2=.2. cos(  2
3)
3=.2. cos  +2
3=.2. cos(  4 3)
On choisie l’origine des phases horizontale et le sens direct dans le sens trigonométrique.
De plus, on constate que les 3 f.e.m produites par le champ magn. d’intensité constante forment un
système triphasé équilibré.
Soit une bobine plate de  spires dans un champ
d’induction magn. avec une vitesse angulaire .
Ce champ magn. tournant pourra être obtenu par
la rotation d’un aimant ou d’un électro-aimant :

III) Technologie de l’alternateur synchrone :
1) Les circuits électriques :
Le rotor est l’inducteur : c’est lui que va absorber la puissance mécanique :
 Le rotor-inducteur de l’alternateur peut être constitué par un aimant permanent = rotor brushless
 Le rotor-inducteur peut aussi être constitué d’un bobinage que l’on fait parcourir par un courant
continu = rotor bobiné.
Cependant, ce dernier doit être alimenté en courant durant son mouvement : il sera donc confronté au
problème des balais et du collecteur.
Ainsi, le cas de l’alternateur brushless correspondra à une simplification de ce cas général.
 le courant inducteur = courant d’excitation
 Par son principe de fonctionnement le rotor-inducteur est aussi appelé roue polaire.
Le stator est l’induit : il produit la puissance électrique.
 Il est constitué de 3 bobinages décalés de 
 , afin de créer des f.e.m ayant ce même décalage.
Remarque : Les champs induits tournent dans le stator à la même vitesse que le rotor. C’est pour cela
que l’alternateur est dit synchrone. Sa vitesse de rotation est notée :  (.1)
2) Les paires de pôles :
=.
p : nombre de paires de pôles
 : fréquence (Hz)
En jouant sur le nombre de paires de pôles, il sera possible de s’adapter à toutes les situations :
- Les centrales thermiques ou à vapeur = alternateur tournant à des vitesses rapides (1500-3000 /min)
- Les centrales hydroélectriques = alternateur tournant à vitesse lente (qq centaine de /min)
On peut constater que le rotor porte le même nombre de paires de pôles que le stator.
3) Symboles électriques :
Avec :
GS : Génératrice synchrone
 : Courant continu
Pour améliorer le fonctionnement du stator il suffit de
mettre 2 bobinages par phase : cela permet de profiter au
maximum du champ magn. et d’augmenter ainsi le
rendement de conversion (sans changer les fréquences
des f.e.m). Si l’un des 2 bobinages induits = pôle nord pour
le rotor alors l’autre présente le pôle sud : paire de pôle.

IV) Fonctionnement de l’alternateur synchrone :
1) Schémas électriques équivalents :
En condition de fonctionnement raisonnable, le comportement électrique de la machine est donné par le
modèle équivalent de Behn-Eschenburg :
Avec :
 : Résistance de l’enroulement
 Pertes par échauffement dans la phase
 = . : réactance synchrone
 Pertes de flux magn. et réaction magn. d’induit
Remarque :
La présence des notations V et J permettent de dresser un modèle dans le cas générale :
- Si alt. monté en étoile : chaque phase délivre V et I.
- Si alt. monté en triangle : chaque phase délivre U et J
Dans la pratique, on préfère les alt. monté en étoile afin de créer le neutre.
D’après la loi des mailles : =+.. +
Or les bobinages induits sont faits de façon à être très peu résistants tels que :  
Donc : =.. +
2) Détermination des grandeurs d’une phase :
a) Force électromotrice :
=...=....
K : constante de la machine = coef. de Kapp
N : nombre de conducteur d’une phase
E : valeur efficace de la f.e.m 
Φ : flux magn.
La valeur efficace de la force électromotrice peut aussi être évalué par mesure à vide, car si l’on supprime la
charge, alors le courant = et donc : =   =
b) La réactance synchrone :
La réactance synchrone se détermine elle-aussi par la mesure : si l’on remplace la charge, par un court-
circuit alors la tension de sortie est annulée et le courant prend une valeur élevée de court-circuit.
On obtient donc : = 0 et =  . Et ainsi : =..  .=
 , Par suite : =
On en conclue que la réactance synchrone d’une phase se mesure à l’aide d’un essai à vide (en circuit
ouvert) suivi d’un essai en court-circuit.
3) Caractéristiques de l’alternateur synchrone :
a) Caractéristique interne :
Caractéristique interne d’un alternateur = courbe () , avec  : courant inducteur (ou d’excitation)
Or  s’obtient à vide donc il s’agit de la
caractéristique () effectuée :
- A vitesse ou fréquence de rotation : =
- A courant induit d’intensité nulle : = 0

b) Caractéristique en court-circuit :
Cette proportionnalité entre  et  est toujours valable dans un alternateur synchrone.
c) Caractéristique externe :
Caractéristique externe = caractéristique en charge de l’alternateur, réalisée à l’aide d’une charge
d’impédance variable mais de () constant. On obtient donc la courbe () :
- A vitesse de rotation =
- A courant d’excitation d’intensité =
- Avec une charge dont cos=
Même si  et cos() peuvent être choisis arbitrairement, la fréquence de rotation est imposée puisqu’elle
conditionne la fréquence  des grandeurs électriques.
d) Diagramme de Behn-Eschenburg :
- Lorsque < : l’alternateur est dit sur-excité (V en avance sur J)  cas d’une charge inductive (a)
- Lorsque > : l’alternateur est dit sous-excité (V en retard sur J)  cas d’une charge capacitive (b)
La courbe  = charge purement résistive
La courbe  = charge résistive et inductive
 La chute de tension est d’autant plus grande que la
charge est inductive.
La courbe  = charge résistive et capacitive
 La chute de tension est d’autant plus petite que la
charge est capacitive
Caractéristique en court-circuit = courbe () tracée :
- A vitesse de rotation : =
- A tension = 0

e) Bilan des pertes et puissances :
 Puissance absorbée : =.= 2..
Même en mode génératrice une puissance électrique . doit être fournie au rotor-inducteur pour créer
l’excitation et le champ d’induction.
 Puissance utile : =..3. cos()
 Les pertes variables : = + =3
2² + .
 Les pertes constantes  = +  mesurables à vide
 Rendement : =
= + + + =  
f) Détermination des pertes constantes dans l’alternateur :
A vide :
0= 0 , car 0= 0, de plus 0= . Donc :  = 2.0.0
Pertes joule au rotor
.