Supraconducteurs et cristaux liquides : histoire d`une

La force de l’analogie en matière condensée
Supraconducteurs et cristaux
liquides : histoire d’une analogie
L’existence possible d’une phase cristal liquide mixte (smectique torsadée) a été mentionnée dès
1972 par P.-G. de Gennes. Issue d’une analogie entre les cristaux liquides et les supraconducteurs,
elle est aujourd’hui une réalité expérimentale. Elle présente des propriétés physiques spectaculaires
liées à la compétition entre ordre lamellaire et arrangement hélicoïdal. La torsion pénètre
la structure lamellaire grâce à un réseau de défauts de la même façon que le flux magnétique
pénètre les supraconducteurs de type II par un réseau de vortex.
L
a matière se présente généra-
lement sous trois états : so-
lide, liquide ou gazeux. Cette
classification est en fait incomplète
car de nombreuses substances orga-
niques ne présentent pas un change-
ment d’état unique (ou transition de
phase) entre le cristal et le liquide,
mais une série de transitions faisant
apparaître des états dont les proprié-
tés physiques sont intermédiaires en-
tre le cristal et le liquide. Ces états,
baptisés cristaux liquides par Leh-
mann au XIX
e
siècle, sont aussi ap-
pelés des mésophases ou états méso-
morphes (du grec signifiant de forme
intermédiaire).
LES CRISTAUX LIQUIDES
Les cristaux liquides (encadré 1)
sont des états intermédiaires qui pos-
sèdent un ordre de position ou
d’orientation à longue portée, mais
pour lesquels le désordre de type
liquide subsiste dans une direction
spatiale au moins. Les cristaux liqui-
des thermotropes (c’est-à-dire dont la
séquence de phase s’obtient par va-
riation de la température) sont cons-
titués de molécules organiques dont
la géométrie conditionne fortement
les structures mésomorphes. Le chi-
miste imagine donc l’architecture
moléculaire de son système afin de
lui donner des propriétés physiques
particulières. Un cœur rigide formé
de cycles aromatiques donne la
forme générale de la molécule. Ces
molécules fortement anisotropes peu-
vent être modélisées par des ellipsoï-
des de révolution de longueur a et de
diamètre b (avec a >> b). Ces molé-
cules allongées en forme de bâton-
nets, dites calamitiques, produisent
généralement des phases nématiques
et smectiques.
Les mésophases nématiques ne
présentent pas d’ordre de position à
longue portée des unités mésogènes
mais un ordre d’orientation à longue
distance. Les axes longs des molécu-
les sont en moyenne parallèles à une
direction macroscopique repérée par
un vecteur directeur n(r). Un tel or-
dre orientationnel donne au système
des propriétés optiques anisotropes
(biréfringence) alors que le manque
d’ordre de position autorise une
grande fluidité. Une rotation de la
molécule autour d’un axe parallèle au
directeur laisse la molécule inchan-
gée contrairement à des rotations
autour d’axes perpendiculaires. L’an-
gle que fait l’axe long de chaque mo-
lécule par rapport au directeur étant
noté θ, la mesure de l’ordre dans la
phase nématique est donnée par
S=1/2
^
3 cos
2
h−1
&
.
Les mésophases smectiques sont
caractérisées par un ordre de position
de type solide dans une direction spa-
tiale et un ordre de type liquide dans
les deux autres ; elles sont donc des
empilements réguliers de couches
liquides. Pas moins de 13 phases
smectiques ont été répertoriées. Du
strict point de vue de la symétrie, on
reconnaît trois ordres smectiques seu-
lement. Dans la phase smectique A
(SmA), la normale Naux couches est
parallèle au vecteur directeur n.Le
milieu est uniaxe. La période des
couches d est en général voisine de la
longueur a d’une molécule dans sa
conformation la plus étendue. La
structure en couche est caractérisée
par une modulation périodique de
toutes les propriétés microscopiques
le long de la direction x du directeur
n. La densité électronique, par exem-
ple, peut être développée en série de
Fourier :
q
~
r
!
=
(
n=1
∞
~
wneinqs⋅r+wn
*e−inqs⋅r
!
avec l
S
=2π/q
S
la longueur d’onde
de la modulation smectique. Le
terme fondamental w
1
du dévelop-
pement de Fourier est égal à zéro
dans la phase nématique et peut
être naturellement choisi comme
paramètre d’ordre smectique :
w
1
(r)=q
1
(r)e
iφ
1
(r)
.
La phase smectique C (SmC) a sa
normale aux couches Ninclinée d’un
angle hpar rapport au vecteur direc-
teur n. Le milieu est optiquement
– Groupe de dynamique des phases conden-
sées, UMR 5581 CNRS, place E. Bataillon,
34095 Montpellier cedex 05.
– Centre de recherche Paul Pascal, UPR
8641 CNRS, avenue A. Schweitzer, 33600
Pessac.
36

biaxe et la période d des couches est
proche de acos h. Enfin, la phase
smectique B hexatique présente un
ordre partiel d’orientation des
liaisons des molécules dans le plan
des couches. Chaque molécule ayant
en moyenne 6 premiers voisins, la
symétrie est d’ordre 6 (hexatique).
Chiralité dans les cristaux liquides
Une molécule chirale est générale-
ment obtenue par l’introduction d’un
Encadré 1
L’ÉTAT CRISTAL LIQUIDE :
UN ÉTAT DE LA MATIÈRE « INTERMÉDIAIRE »
Friedrich Reinitzer, botaniste autrichien, travaillait en 1888 sur
la fonction du cholestérol dans les végétaux. Il constate qu’à
145,5°C son cristal devient trouble et fluide à la fois, puis se
transforme en un liquide complètement transparent à 178,5°C.
Surpris, il envoie ses échantillons chez le physicien allemand
Otto Lehmann. Celui-ci se convainc que le « liquide trouble »
de Reinitzer constitue effectivement une phase homogène. De
plus, la manière dont il affecte la propagation de la lumière est
typique du comportement d’un cristal, d’où le nom finalement
choisi par Lehmann pour qualifier ce nouvel état de la
matière : cristal liquide. Toute une zoologie de mésophases est
finalement observée et Georges Friedel, en 1922, propose une
classification des mésophases toujours en vigueur.
Exemple de molécule cristal liquide (7S5) modélisée par un ellipsoïde de révolution de longueur a :
Représentations schématiques de différents états ou phases :
État liquide Phase nématique
Phase smectique A Phase smectique C
La force de l’analogie en matière condensée
37

carbone à quatre substituants diffé-
rents (appelé carbone asymétrique).
Elle ne peut donc pas être super-
posée à son image dans un miroir. En
présence de chiralité, une phase né-
matique présente une torsion sponta-
née d’axe perpendiculaire au vecteur
directeur. Une telle phase nématique
torsadée (figure 1), découverte au
XIX
e
siècle dans des dérivés du cho-
lestérol, est appelée phase cholestéri-
que (N*). Dans cet état, la direction
de l’alignement moléculaire moyen
tourne de façon hélicoïdale le long de
l’axe z. Le pas P (distance entre
plans équivalents) dépend de la
concentration et du degré de chiralité
des molécules.
Dans un smectique A, la normale
aux couches Nest confondue avec le
vecteur directeur net la période des
couches d est constante. La torsion et
la courbure ne peuvent pas se déve-
lopper à une échelle macroscopique.
Le lecteur s’en convaincra en es-
sayant de tordre un annuaire télépho-
nique, qui constitue un modèle de
smectique rudimentaire, les couches
de celui-ci étant matérialisées par les
pages de celui-là. La torsion ne va ja-
mais très loin, sauf si l’on parvient à
déchirer le bloc de pages. Cette dé-
chirure s’identifie alors aux disloca-
tions vis des plans smectiques que
nous décrirons plus loin. La pénétra-
tion de la torsion nécessite des épais-
seurs de couches non uniformes ou la
présence de défauts comme des dis-
locations. Dans une phase smectique
C, la normale aux couches n’est plus
confondue avec le directeur. Ce de-
gré de liberté supplémentaire autorise
la torsion macroscopique : le direc-
teur développe une structure hélicoï-
dale d’axe perpendiculaire aux cou-
ches (phase SmC*).
Comment introduire de la torsion
dans un smectique ?
Le glissement d’une partie du ma-
tériau smectique perpendiculairement
aux couches induit un défaut appelé
ligne de dislocation (figure 2a). Une
boucle tracée autour de cette disloca-
tion traverse nécessairement un nom-
bre entier b de couches (best appelé
le vecteur de Burgers). La phase du
paramètre d’ordre smectique varie de
2p×b sur un tel circuit ; comme les
plans tournent de façon hélicoïdale, ce
défaut est appelé dislocation vis.
Imaginons un empilement régulier
dans un plan de dislocations vis équi-
distantes et parallèles (figure 2b). Les
lignes en trait plein et en pointillé
correspondent à deux réseaux de cou-
ches en avant et en arrière du plan.
Ce plan est en fait un joint de grain
qui produit une rotation globale en-
tre ces deux réseaux d’un angle D.
Une relation géométrique simple re-
lie Dà la période smectique (d) et à
la distance entre deux lignes de dis-
location vis (l
d
). La torsion dans un
smectique résulte donc d’un empile-
ment régulier de dislocations vis.
UNE SURPRENANTE ANALOGIE
Cristaux liquides et supraconduc-
teurs : quel rapport peut-il y avoir en-
tre deux domaines aussi différents de
la physique de la matière condensée ?
Les premiers affichent l’heure, les se-
conds conduisent le courant électri-
que sans résistance dans les instru-
ments de haute technologie ; ceux-ci
opèrent à température ambiante,
ceux-là ne supportent que les très
basses températures ; d’un côté des
molécules organiques à l’architecture
savamment étudiée, de l’autre des
métaux purs ou des alliages miné-
raux.
La base de l’analogie est simple :
les phases ordonnées du smectique A
et du supraconducteur sont caractéri-
sées par un paramètre d’ordre com-
plexe ψ. Pour le supraconducteur, le
paramètre d’ordre est la densité de
paires d’électrons supraconducteurs
(paires de Cooper) tandis que, pour le
smectique, il s’agit de la modulation
périodique de densité associée à l’or-
dre smectique. Le développement
Figure 1 - Représentation schématique de la
phase cholestérique. Le directeur ntourne de fa-
çon hélicoïdale le long de l’axe z.
Figure 2 -(a) Représentation schématique d’une ligne de dislocation vis obtenue par glissement d’une
partie du matériau smectique perpendiculairement aux couches. (b) Paroi de torsion formée d’un em-
pilement régulier dans un plan de lignes de dislocations vis parallèles à une distance l
d
.
38

complet de l’analogie, par comparai-
son des hamiltoniens décrivant les
deux systèmes (encadré 2), montre en
outre que le champ de directeur n(r)
(représentant l’axe moyen des molé-
cules de cristal liquide) s’identifie au
potentiel vecteur magnétique Ades
supraconducteurs. Alors que la tor-
sion du directeur correspond à l’in-
duction magnétique B, le champ H
s’identifie à la chiralité.
Ainsi, lorsque le chimiste « chira-
lise » un cristal liquide par l’intro-
duction d’un carbone asymétrique, il
produit un effet analogue à la réponse
d’un matériau supraconducteur à un
champ magnétique extérieur. Le cho-
lestérique est alors l’analogue du
conducteur normal dans un champ
magnétique extérieur. L’expulsion de
la torsion qui apparaît à la transition
cholestérique-smectique A est l’ana-
logue pour un cristal liquide de l’ef-
fet Meissner (expulsion de l’induc-
tion magnétique).
L’analogie suggère l’existence
d’une phase intermédiaire entre la
phase cholestérique et la phase smec-
tique A habituelle, analogue de la
phase de flux d’Abrikosov des supra-
conducteurs de type II. Dans cette
phase mixte la torsion pénétrerait la
structure grâce à un réseau de défauts
tout comme le flux magnétique pénè-
tre les supraconducteurs par un
réseau de lignes de tourbillon ou vor-
tex. Les vortex ont, comme analo-
gues, les lignes de dislocation vis
dans les cristaux liquides chiraux,
mais rien de semblable à la phase
mixte n’était connu dans les cristaux
liquides en 1972. Le tableau ci-
dessus résume l’analogie entre les
grandeurs physiques des deux domai-
nes : supraconducteurs et cristaux
liquides.
LA PHASE À TORSION PAR JOINT
DE GRAIN (TGB)
L’espoir revient en 1988 lorsque
Scott Renn et Tom Lubensky identi-
fient la forme que devrait prendre la
phase mixte dans le cristal liquide.
Combinant la démarche propre aux
supraconducteurs et les particularités
des cristaux liquides, ils aboutissent à
trois conclusions théoriques :
1) Ils proposent l’existence d’une
phase nommée TGB (pour Twist
Grain Boundary phase) analogue de
la phase de flux d’Abrikosov (figure
3). La structure du réseau de disloca-
tion vis est par contre différente de la
structure triangulaire du réseau de li-
gnes de tourbillons d’Abrikosov. La
torsion macroscopique résulte d’un
empilement régulier de joints de
grains équidistants et séparés d’une
distance l
b
. Chaque joint de grain est
formé d’un réseau de lignes de dislo-
cations vis parallèles et équidistantes.
La distance entre deux lignes adja-
centes est égale à l
d
. La structure
TGB est donc caractérisée par 5 pa-
ramètres : la taille des blocs smecti-
ques (l
b
), la distance entre deux li-
gnes de dislocations vis (l
d
), la
période des couches smectiques (d),
le pas de l’hélice (P) et l’angle de ro-
tation entre deux blocs smectiques
adjacents (D). Ces 5 paramètres sont
reliés par deux relations structurales :
d
2l
d=sin D
2et lb/P =D/2 p
La nature de la phase TGB dépend
de la valeur de D=2pa.Siαest ir-
rationnel, la phase est incommen-
surable le long de l’axe de l’hélice.
Si aest rationnel (a=m/n), la
structure est commensurable et pré-
sente un axe de torsion d’ordre n.
Elle est périodique de période
nl
b
= mP le long de l’axe de torsion.
Si la symétrie de torsion n’est pas
permise par la cristallographie (c’est-
à-dire n 72, 3, 4 ou 6), l’ar-
rangement est quasi-cristallin et
incommensurable dans le plan
perpendiculaire à l’axe hélicoïdal.
2) Les phases TGB doivent appa-
raître dans la région du diagramme
de phase où se rencontrent trois pha-
ses cristal liquide chirales : le néma-
tique torsadé N*, le smectique A et le
smectique C (point dit NAC chiral).
C’est à cet endroit que la condition
de type II est satisfaite.
3) Trois types de phases TGB sont
prévus : TGB
A
, TGB
C
et TGB
C*
pour des structures locales de type
SmA, SmC et SmC* respectivement.
En 1989, John Goodby et ses col-
laborateurs synthétisent une nouvelle
molécule chirale dont une phase pos-
sède les propriétés optiques et struc-
turales de la phase TGB
A
incommen-
surable. A la lumière des prédictions
théoriques de Renn et Lubensky et
de la découverte expérimentale de
Goodby, Tinh Nguyen synthétise,
avec son équipe du centre de recher-
che Paul-Pascal (Pessac), de nouvel-
les séries de cristaux liquides chiraux
combinant une forte chiralité et un
polymorphisme NAC. Après plu-
sieurs mois de recherche, la décou-
Supraconducteurs Cristaux liquides
ψ: densité des paires de Cooper ψ: paramètre d’ordre smectique
A : potentiel vecteur magnétique n : directeur
B = rot A : induction magnétique n.rot n : torsion
H=B/µ: champ magnétique h : chiralité
Conducteur normal Phase nématique
Conducteur normal en champ magnétique Phase cholestérique
Phase Meissner Phase smectique A
Effet Meissner Expulsion de la torsion
λ
2
: longueur de pénétration de London λ
2
: longueur de pénétration de la torsion
ê: longueur de cohérence ê: longueur de corrélation du paramètre d’ordre
Lignes de tourbillon (vortex) Lignes de dislocation vis
Réseau de flux d’Abrikosov Phase smectique à torsion par joint de grain (ou
TGB)
La force de l’analogie en matière condensée
39

verte de la phase TGB
C
viendra de la
série ayant pour formule générale :
*
Toute la complexité de la phase
TGB réside dans cette compétition entre un ordre hélicoïdal (comme dans le cholestérique) et un ordre en
couche (comme dans le smectique
habituel). L’étude structurale de la
phase TGB doit donc se faire princi-
palement par la mesure de trois para-
mètres. Tout d’abord, il est nécessaire
Encadré 2
UNE SURPRENANTE ANALOGIE
La densité d’énergie libre associée à la transition nématique-
smectique A peut être développée en puissances paires de
u
w
u
(paramètre d’ordre smectique). En incluant les termes en
gradient et les fluctuations du directeur nématique
dn⊥=n(r)−n0(n07zˆ), la fonctionnelle de Landau-Ginzburg
s’écrit :
DFN−SmA =1
2
*
$
r
u
w
u
2+u
2
u
w
u
4+C{
u
∇zw
u
2
+C⊥
u
~
∇⊥−iqsdn⊥
!
w
u
2+
K1
~
div dn⊥
!
2+K2
~
zˆ, rot n
!
2+K3
~
∇zdn⊥
!
2
%
d3x
(1)
Les trois derniers termes décrivent l’énergie élastique de
déformation du directeur (énergie de Frank). K1,K
2et K3sont
respectivement les constantes élastiques de déformation en
éventail, de torsion et de courbure. A cause de l’anisotropie
du cristal liquide, les termes en gradient présentent des
coeffıcients anisotropes (C{7C⊥)le long des directions
parallèle et perpendiculaire au directeur n. Un simple
changement d’échelle anisotrope permet de retrouver une
écriture isotrope (C{7C⊥).
L’équation (1) présente de fortes analogies avec la
fonctionnelle de Landau-Ginzburg décrivant la transition
conducteur normal-supraconducteur dans les métaux :
F=
*
$
r
u
w
u
2+u
2
u
w
u
4
+1
4m
u
~
\∇−i2e
cA
!
w
u
2+1
8pµ
~
rot A
!
2
%
d3x (2)
Dans l’équation (2), west le paramètre d’ordre
supraconducteur (densité de paires de Cooper), Aest le
potentiel vecteur magnétique (analogue au directeur n),mete
la masse et la charge de l’électron, \est la constante Planck,
c est la vitesse de la lumière et µla perméabilité magnétique
du métal. La comparaison des équations (1) et (2) montre que
rot n est analogue au champ magnétique B=rotA. La torsion
(n.rotn) et la courbure (n×rot n) sont les composantes
parallèle et perpendiculaire du directeur. Tout comme les
supraconducteurs expulsent le champ magnétique rot A (effet
Meissner), les smectiques expulsent la torsion et la courbure.
Les expériences confirment que les constantes élastiques de
torsion et de courbure (K
2
et K
3
) divergent à l’approche du
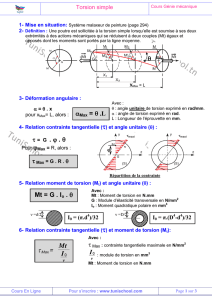
smectique. Les diagrammes de phase ci-dessous résument
l’analogie pour les supraconducteurs de type I et de type II :
40