MISE EN EQUATION D`UN SYSTEME MECANIQUE EN ROTATION

MISE EN EQUATION D'UN SYSTEME MECANIQUE EN ROTATION
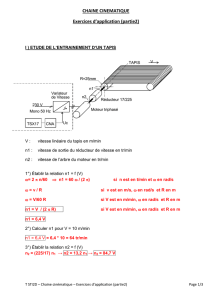
Pour le système mécanique suivant :
→ Ecrire les équations de bilan énergétique et en déduire l'équation différentielle liant
le couple Γm appliqué à l'entrée et la vitesse angulaire de sortie ω.
→ Déterminer la fonction de transfert correspondante (entrée Γm, sortie Ω).
Le réducteur a un rapport (n), ce qui signifie que si on note ωm la vitesse de rotation de l'arbre
moteur, alors on a : ω = ωm / n
Jm
fm
f
J
ω
Γm
Réducteur

RELATION entre le principe fondamental de la dynamique et les bilans à
partir de l'énergie cinétique
Pour les systèmes mécaniques en translation on considère un élément de masse m, et
pour les systèmes en rotation un élément d'inertie J.
Bilan général :
Σ−Σ+ Σ−Σ+
=ji
ji
cinétique MM
QQ
dt
dE
Pour un système en translation :
Ecinétique = 2
1mv2où v est la vitesse du système,
Q = quantité de mouvement = v.F où F est une force appliquée au système.
Le bilan s'écrit donc :
ji vFvF
dt
mvdΣ−Σ+=
2
2
1
i.e.
[]
ji
2FFv
dt
dv
m
2
1Σ−Σ+= (la vitesse est la même pour un élément de masse m donnée)
i.e.
[]
ji FFv
dt
dv
v2m
2
1Σ−Σ+=
Après simplification par v, on obtient :
ji FF
dt
dv
mΣ−Σ+=
c'est-à-dire le principe fondamental de la dynamique.
Pour un système en rotation :
Ecinétique = 2
1Jω2où ω est la vitesse de rotation du système,
M = moment cinétique = ω.Γoù Γ est un couple appliqué au système.
Le bilan s'écrit donc :
ji
2
dt
J
2
1
dΓωΣ−ΓωΣ+=
ω
De la même manière que pour le système en translation, on obtient :
ji
dt
d
JΣΓ−ΣΓ+=
ω
c'est-à-dire le principe fondamental de la dynamique.

CORRECTION
Détermination du nombre d'équations différentielles à considérer.
On repère 2 éléments qui stockent/déstockent l’énergie :
L'arbre moteur d'inertie Jm→ sous-système I
L'arbre de sortie d'inertie J → sous-système III
On repère 1 élément qui transmet la puissance sans pertes :
Réducteur de rapport (n) → sous-système II
Bilan pour le sous-système I
On utilise le principe fondamental de la dynamique. On cherche les termes faisant
varier la vitesse de rotation de l'arbre moteur, ωm :
• entraînement de l’arbre moteur : couple Γm, signe "+" (l'entrainement fait
augmenter la vitesse).
• frottements visqueux proportionnels à la vitesse : fmωm, signe "-"
(résistance à la rotation qui fait diminuer la vitesse).
• Le couple à l’interface arbre moteur (sous-système I) /réducteur (sous-
système II), ΓI/II. Fait-il ↑ou ↓ la vitesse ? L’arbre moteur entraîne l’arbre
de sortie, ce qui se traduit par une résistance à l’entraînement de l’arbre de
sortie vue par l’arbre moteur à travers le réducteur sous la forme d’un
couple résistant ΓI/II ⇒ ΓI/II a un signe "-" (négatif).
D'ou l'équation différentielle suivante :
() () () ()
ttft
dt td
JIIImmm
m
m/
Γ−−Γ+=
ω
ω
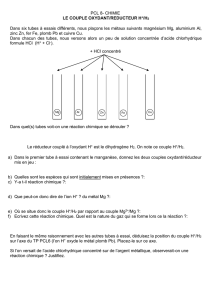
Système
II S
y
stème III
Système I
Jm
fm
f
J
ω
ΓmΓI/II
ΓII/III

Bilan pour le sous-système III
On utilise le principe fondamental de la dynamique. On cherche les termes faisant
varier la vitesse de rotation l'arbre de sortie , ω :
• frottements visqueux proportionnels à la vitesse : f*ω, signe "-" (résistance
à la rotation qui fait diminuer la vitesse).
• Le couple à l’interface réducteur (sous-système II) / arbre de sortie (sous-
système III), ΓII/III. Fait-il ↑ou ↓ la vitesse ? L’arbre de sortie est entraîné
par l’arbre moteur. Par conséquent, ΓII/III est l’effet d’entraînement de
l’arbre moteur sur l’arbre de sortie à travers le réducteur ⇒ ΓII/III a un
signe "+" (positif).
D'ou l'équation différentielle suivante :
() () ()
tft
dttd
JIIIII
ω
ω
−Γ= /
Bilan pour le sous-système II
La puissance à l’entrée du réducteur est intégralement transmise à la sortie du
réducteur, c'est-à-dire :
() () () () tttt IIIIIIIIm // Γ=Γ
ωω
avec la propriété du réducteur : () ()
nt
tm
ω
ω
=
Equations différentielles de bilan et calcul de la fonction de transfert :
() () () () ()
() () () ()
( ) () () () ()
() ()
=
Γ=Γ
−Γ=
Γ−−Γ=
nt
t
ttttII
tft
dttd
JIII
ttft
dt td
JI
m
IIIIIIIIm
IIIII
IIImmm
m
m
ω
ω
ωω
ω
ω
ω
ω
Avec
//
/
/
[1]
Pour obtenir la fonction de transfert
()
()
p
p
m
Γ
Ω, on peut directement prendre la transformée de
Laplace, plutôt que de passer par l’équation différentielle entrée/sortie.
TL( [1] ) ⇔
() () [] () () ()
() ()
[] () ()
() ()
() () () ()
ΓΩ=ΓΩ Ω=Ω Ω−Γ=−Ω Γ−Ω−Γ=−Ω pppp
pnp
pfpppJ
ppfpppJ
IIImIIIII
m
IIIII
IIImmmmmm
//
/
/
0
0
ωω

TL( [1] ) ⇔
() () () () ()
() () () ()
() ()
() ()
() () ()
Γ
=Γ
Ω
Ω
=Γ
Ω=Ω Γ=Ω+−Ω Γ=Γ+Ω+−Ω
np
p
p
p
p
pnp
ppfJpJp
pppfJppJ
IIIII
IIIII
m
III
m
IIIII
mIIImmmmmm
/
//
/
/
0
0
ωω
⇔ () () () () () () ()
[]
0
1
0
ωω
JpfpJp
n
JnpfnppJp mmmmm −Ω+Ω+−Ω+Ω=Γ
⇔ () () () () () 00
ωω
n
J
Jp
n
f
nfpp
n
J
nJp mmmmm −−Ω ++Ω +=Γ
⇔
() () () ()
00
ωω
n
J
Jp
n
f
nfp
n
J
nJp mmmmm ++Γ= ++ +Ω
La transformée de Laplace du système [1] devient :
()
() () () ()
se libree la réponcaractéris
mm
mm
m
se forcéee la réponcaractéris
mm
mn
f
nfp
n
J
nJ
n
J
J
p
n
f
nfp
n
J
nJ
p
p
++ +
+
Γ
+
++ +
=
Γ
Ω00 11
ωω
Le terme correspondant à la réponse libre est noté "PCI" pour Polynôme aux
Conditions Initiales.
Le terme correspondant à la réponse forcée, noté "FT", est la Fonction de Transfert du
système. Il correspond au cas où l'on suppose les conditions initiales identiquement nulles (CI
≡ 0), c'est-à-dire à PCI = 0.
Dans notre cas, CI ≡ 0 signifie ωm(0)=0 et ω(0)=0.
Lorsque l'on cherche la FT d'un système, on suppose les CI ≡ 0 dès le début du calcul
de la transformée de Laplace. Cela permet de simplifier les calculs.
Remarque sur le réducteur :
On a ω(t) = ωm(t) / n
i.e.
()
()
np
p
m
1
=
Ω
Ω
Or
()
() () () ()
()
p
p
p
p
p
p
m
m
mm Γ
Ω
Ω
Ω
=
Γ
Ω.
D’où
()
()
++ +
=
++ +
=
Γ
Ω
22
11
nf
fp
n
J
J
n
f
nfp
n
J
nJ
n
p
p
mmmm
m
m