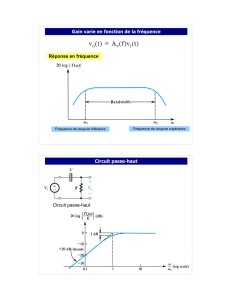
EIS App Systèmes et Composants Electroniques Grenoble INP

GD Partie II 1/37
E I S
App
Systèmes
et
Composants
Electroniques
Grenoble INP
ESISAR
Cours EE470
ELECTRONIQUE
de
PRECISION
Pierre Simon De Laplace (Français, 1749-1827)
Hendrik Wade Bode (USA-1905-1982)
Paul Dirac (UK – 1902-1984)
Harry Nyquist (1889-1976)
Responsable : Dehay
Auteurs : Guy Dehay
Imprimé le mercredi 19 avril 2017

EE479 Electronique de précision SCE
GD Amplificateur d’instrumentation 2/17
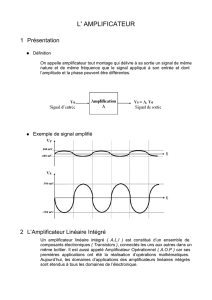
I Présentation
I.1/ Introduction
Aujourd’hui le nombre de chaîne de mesures utilisées par des
systèmes industriels est très important dû à l’accroissement des
systèmes automatisés. En effet ces dispositifs nécessitent pour
leur bon fonctionnement la mesure de grandeurs physiques avec
des précisions toujours plus grandes. L’électronique mise en
œuvre qui était réservée il y a encore peu aux laboratoires se
retrouve dans un grand nombre de réalisations industrielles
actuelles (cimenterie, centrale électrique, traction ferroviaire…).
Cela a été possible par un accroissement des qualités de
l’électronique analogique et du développement de
l’informatique.
I.2/ Quel type d’électronique
L’électronique qui nous intéresse est celle constitutive des
chaînes d’acquisitions. C’est une électronique analogique des
faibles niveaux qui vient récupérer des signaux électriques issus
de capteur. Ces signaux sont porteurs d’une information
correspondant à une grandeur physique (Fig. 1). Cette
électronique doit adapter les niveaux électriques sans déformer
l’information pour que celle-ci puisse être manipulée plus
simplement (niveaux de tension élevés, numérisation, transport
par différents canaux…)
Grandeur physique
Système 
Signaux faibles niveaux
Signaux forts niveaux
Signaux utiles
Capteur
Conditionneur
Amplificateur
Traitements
Fig. 1 : Chaîne d’acquisition simple.
I.3/ Problématique
Plusieurs difficultés coexistent pour la mise en œuvre de cette
électronique de précision.
 Le signal informatif est souvent minuscule vis à vis des
grandeurs avoisinantes.
 La présence de perturbations extérieures est permanente ce qui
détériore la mesure.
 Les constituants de la chaîne d’acquisition elle-même ne sont
pas parfaits.
Nous parlerons de conditionneur, d’amplificateur, de bruit. Les
parties capteurs sont vues en physique avec M. Lemaître et la
limitation des perturbations extérieures en CEM avec
M. Grosjean.
Les pages qui vont suivre sont là pour donner des réponses aux
problèmes que posent la mise en œuvre de certains éléments
d’une chaîne d’acquisition. Il n’y a pas en générale de solution
parfaite car les contraintes techniques et économiques imposent
des compromis.
II Notions primordiales
II.1/ Mode commun, mode différentiel (série)
L’information est transportée par la différence des tensions
(Fig. 2) dont le support matériel sont les conducteurs (1) et (2).
Ils sont soumis à des tensions parasites vp1 et vp2.
Il y a une perturbation de mode commun lorsqu’un parasite
identique apparaît à la fois sur les deux conducteurs. Les deux
tensions varient simultanément par rapport à la masse (fig. 2a).
vp1 = vp2
Il y a perturbation différentielle ou mode série lorsque le
parasite apparaît comme une différence de potentiel entre les
conducteurs.
vp1  vp2
vp2
vp1
(1)
(2)
masse
parasite
vp2
vp1
(1)
(2)
vp2 - vp1
parasite
(a)
(b)
vp1 = vp2
vp1  vp2
Fig. 2 : types de perturbations en : (a) mode commun ; (b) mode série.
La tension parasite de mode commun est par définition :
vp_mc = ½ (vp1 + vp2)
vp_mc = vp lorsque vp1 = vp2 = vp
La tension parasite différentielle est par définition :
v p_d = vp2  vp1
v p_d = 0 lorsque vp1 = vp2 = vp
Conclusion
Lorsque les parasites sont identiques sur les conducteurs du
signal, la perturbation est uniquement en mode commun.
Lorsque les parasites ont des amplitudes différentes sur chacun
des conducteurs, il apparaît en plus d’une tension parasite en
mode commun, une perturbation en mode différentiel.
Nous verrons que l’utilisation d’un amplificateur différentiel
permet de s’affranchir d’une grande part des perturbations en
mode commun puisqu’il n’amplifie que la différence des
tensions d’entrées. Cependant, dans la pratique il reste
légèrement sensible au mode commun, sensibilité qu’on
quantifie avec le taux de réjection du mode commun.
La réduction des parasites en mode différentiel est plus délicate.
Le filtrage est un des moyens utilisé. Il reste qu’une bonne
conception électronique ainsi qu’une bonne protection CEM
évite la présence de ces perturbations.
III Conditionneurs
III.1/ Rôles
Les qualités et la souplesse de l'électronique font que toutes
informations nécessaires au traitement d'un processus qui sont
des grandeurs variées (niveau d'eau, pression, contrainte

EE479 Electronique de précision SCE
GD Amplificateur d’instrumentation 3/17
mécanique …) sont toutes transformées en une information
électrique. Cependant, avant de manipuler une tension qui est le
support de l'information dans la chaîne d'acquisition, nombre de
capteurs fournissent une information électrique d'un autre type
comme la variation de résistance ou un générateur de
courant….Le rôle du conditionneur est d'adapter la grandeur
électrique de sortie du capteur en une tension qui pourra ensuite
être amplifiée. Des compensations et/ou des linéarisations sont
quelquefois intégrés dans les conditionneurs.
III.2/ Capteurs : Résistifs
Quelles mesures ?
On distingue deux types de mesures de résistances.
Mesure de la résistance R(m)
A travers la mesure de R, on déduit directement par le biais
d'une table de correspondance la valeur de la grandeur physique
recherchée. (ex: la mesure de température avec une sonde de
platine PT100). Un montage "quatre fils" alimenté par une
source de courant convient. Il s'agit d'une mesure absolue.
Mesure d'une variation de résistance R(m)
C'est au travers des variations d'une résistance R(m) qu'on
retranscrit les variations de la mesurande m. La mesure des
variations de résistance d'une thermistance permet la mesure
d'une faible variation de température T autour d'une
température fixée To. On utilisera alors un pont de Wheatstone.
Il s'agit d'une mesure relative.
Montage 4 fils
La résistance de mesure R(m) est alimentée par une source
(2 fils) de courant I (constant). Puis avec 2 autres fils on vient
prélever la ddp aux bornes de R(m). L'impédance mis en
parallèle avec R(m) est la mise en série des fils d'amenés Rf et
de l'impédance d'entrée de l'instrumentation Ri.
I
R(m)
Ri
Rf
Rf
Instrumentation
Alimentation
en courant
vm
Fig. 3 : Montage 4 fils.
La résistance véritablement mesurée est :
I.v if
)m( if
)m( RR2R )RR2.(R
m
Dans le cas où R(m) << 2Rf + Ri on a
Vm = R(m) I
Remarque
Il est important de soigner la "connectique" de façon à limiter le
plus possible la chute de tension de contact au niveau de la prise
de mesure.
Pont de Wheatstone déséquilibré
Le pont de Wheatstone est un réseau de résistances qui permet
avec une tension intermédiaire d'exprimer des conditions sur les
résistances constituant le pont.
RthB
RthA
A
R3
R4
B
vm
R1
R2
C
D
E
D
EthA
EthB
A
B
vm
Fig. 4 : Pont de Wheatstone.
Les deux branches en parallèle CD sont alimentées par la même
source de tension E. On sépare intellectuellement les deux
branches et elles sont remplacées par leurs générateurs de
Thévenin équivalent vue de AD et BD respectivement. On a
alors
EEEv )RR)(RR( RRRR
RRR RRR
m4321
4132
43
4
21
2
1er cas : Une seule résistance variable
Le pont est constitué de trois résistances identiques fixes et
d'une jauge de contrainte :
R1 = R3 = R4 = Ro et R2 = Ro +R
On obtient alors
EEv )RR2(R2 RR
)RR)(RRR( RRR)RR(
moo
o
oooo
oooo 
4
E
1
4
E
1
R2R4 R
m2
o
R2 R
o
RR
oEv 
Cette relation n'est pas linéaire. Cependant pour de faible valeur
de , on a
4
E
4
E
24
E
1
m)1(v 2
soit
4
E
RR
mo
v
Amélioration
Il existe des montages avec des AOP qui permettent de
linéariser la relation. Cependant, la présence de ce composant
actif amène son lot de désagréments (bruit de fond, courant de
polarisation, …). Cf. TD.
2ème cas : Montage Push-Pull, 4 résistances variables.
Sur le même montage, on utilise cette fois-ci 4 éléments
variables qui sont montés de telle sorte que les variations de
chacun accroissent globalement l'écart du pont.
R2 = R3 =  R1=  R4
On trouve alors
Ev
Ev
2
o
2
o
2
o
2
o
2
o
oooo
2
o
2
o
R4
)RRR2R()RRR2R(
m
)RRRR)(RRRR( )RR()RR(
m
Ev o
RR
m
La relation est linéaire mais on a supposé que les quatre jauges
avaient des variations identiques, ce qui n'est pas vrai.
III.3/ Capteur : Réactifs
En préambule, il faut noter que l'information apportée par un
changement d'élément réactif peut avoir deux supports
différents.
 Soit sur l'amplitude au moyen d'un pont d'impédance.

EE479 Electronique de précision SCE
GD Amplificateur d’instrumentation 4/17
 Soit sur la fréquence, en modifiant une cellule d'accord d'un
oscillateur.
Pont d’impédance
RthB
ZthA
A
Ro
Ro
B
vm
Z1
Z2
C
D
e(t)
D
ethA
ethB
A
B
vm
Fig. 5 : Pont de Wheatstone.
Une tension sinusoïdale alimente le pont. L'information est la
tension vm de déséquilibre du pont. Avec la représentation de
Thévenin (Fig. 5) on a.
o
2
1
thB
)t(
2
1
thB
ZZ
.ZZ
thA
)t(
ZZ
Z
thA
RRee
Zee 21
21
21
2
Le choix d'une mesure en tension ou en courant est réalisé par la
connaissance de l'impédance équivalente du pont Z et de Zm
l'impédance d'entrée de l'appareil de mesure associé avec une
capacité parasite Cp. A la fréquence de travail qui nous intéresse
on a ZcP >> Zm d'où Zin = Zm.
Mesure en tension
Zm >> Z alors vm  eth
Mesure en courant
Zm << Z alors im 
Z
eth
Z
eth
A
B
vm
Zm
Cp
im
Instrumentation
Fig. 6 : Schéma de Thévenin
équivalent au pont de Wheatstone.
Cpm
Cpm
o
21
21
21
12
ZZ .ZZ
in
2
R
ZZ .ZZ
thBthA
(t)
ZZ ZZ 2
1
thBthAth
Z
ZZZ
eeee
C'est la connaissance du capteur qui permettrait de déterminer le
type de mesure à réaliser.
Applications : Capteurs inductifs
La fréquence d'utilisation est de 10 kHz et la bobine est de
l'ordre de 30 mH. La capacité Cp est de 10 pF. Soit
e(t) = Ecos(t)
Z1 = Z2 = L = 30.210 = 1,88 k d'où ZthA = 942 
Zcp = (Cp.)1 = (10.1012. 210.103)1 = 1,6 M
La mesure en tension s'impose puisque il est aisé d'avoir une
impédance d'entrée d'amplificateur voisine du M et que Zcp et
du même ordre de grandeur. Nous sommes en présence d'une
mesure en tension.
(t)
ZZ ZZ 2
1
(t)
th
(t)
m.eev 21
12
Afin de linéariser la mesure, on utilise deux inductances de
mesures montées en push-pull afin d'augmenter le déséquilibre
du pont fig. 7.
fig. 7 : Double inductances avec noyau mobile.
On a alors
thA
ZZ
m
voùdZetZ  'ZZZZ 21
Au premier ordre les inductances sont proportionnelles au
déplacement d'un noyau ferromagnétique, alors
)ax1(LL
e.x.aevoù'd)ax1(LL
o2
)t()t(
LL LL 2
1
)t(
mo1 21
12
La tension mesurande est finalement
2
E
mm
)t(
maSoùx.SVavec)tcos(Vv 
Remarque
La tension vm est finalement une modulation d'amplitude sans
porteuse du signal d'alimentation du pont e(t). L'amplitude est
modulée par la position du noyau. Il est alors possible d'utiliser
une détection synchrone pour retrouver x(t).
Dans le cas d'un capteur de type capacitif, la mesure se réalise
plutôt en courant.
Détection synchrone
Un détecteur synchrone (Fig. 8) est constitué d'un oscillateur
sinusoïdal qui alimente le pont de Wheatstone et un déphaseur
de  (réglable) en parallèle.
vo1(t)
vo(t)
Pont
X
Filtre
passe bas
Déphaseur 
x(t)
vm(t)
Oscillateur
cos(t)
e(t)
e(t)
ed(t)
Fig. 8 : Détection synchrone.
Les tensions e(t) et ed(t) s'expriment
)tcos(.E oo )t(e 
)tcos(.E oo )t(ed
Comme il est montré plus haut le signal vm(t) est modulé en
amplitude (sans porteuse) par x(t). Le pont apporte un
déphasage .
)tcos().t(x.Sv o )t(
m
Le signal modulé vm est multiplié par un signal déphasé de 
avec la porteuse. Le réglage du déphaseur  égale à  permet
d'obtenir cos = 1.  [V-1]
)t2cos(
2
SE
x
2
SE
)tcos(E)tcos(xS
)t(e)t(vv
o
o
)t(
o
ooo
)t(
dm1o
Le signal obtenue traverse alors un filtre passe bas qui élimine
la partie en 2o pour ne conserver que le signal informatif.

EE479 Electronique de précision SCE
GD Amplificateur d’instrumentation 5/17
)t(
o
ox
2
SE
v
Il faut remarquer que le spectre de x(t) doit être très inférieur à
la pulsation de la porteuse o.
III.4/ Détection de phase
On veut concevoir une chaîne de mesure de différence de phase
sur des signaux noyés dans du bruit et fluctuant en amplitude
dans une large bande de fréquence. Pour cela on utilise une
détection synchrone (Fig. 9) dont le déphaseur est un système à
retard variable . Le filtre est remplacé par un intégrateur suivi
d'un détecteur de zéro.
p(t, )
m() = Mcos
X
Retard 
e2(t) = E2cos(t+)
e1(t-)
e1(t) = E1cos(t)
Détecteur
de zéro
Fig. 9 : Détection de phase par détection synchrone.
Un premier signal pris pour référence passe par le retard.
)tcos(.E )(
o1
)t(
1
e 
Le produit de e1 et e2 (le deuxième signal de mesure) donne
VMavec
tMtp
ttEEtp
EE
ooo
oo
2
)(
21
21
)cos()2cos(),(
)cos()cos(.),(
L'intégration de p(t,) déprend la valeur moyenne du signal.
 2
T
0
T
1Tavecdt).,t(p)(m
m() = M.cos( +  )
Le réglage du retard  =  jusqu'à obtenir m() = 0 permet la
mesure du déphasage .
 kavec)1k2( 2
oo
Avoir k différent de zéro représente une mesure de phase dans
laquelle il y a k périodes complètes plus le déphasage. En
supposant k = 0, on a alors
1
2 bavecb o
Le signe devant /2 représente l'ordre des signaux ou bien la
référence des signaux. La distinction pratique s'opère par la
mesure du signe de la variation de m() au voisinage de o.
m() = M cos()
½
M cos()
½
3/2 
Changement de repère
b = -1
b = 1
Fig. 1: m().
On effectue un changement de variable où ' est au voisinage de
zéro en posant
 = o + ' soit ' =    o
m(' = M cos(+oo+o') = M cos(
2
b
+ o')
m(' = b M sin(o')
d)'(dm
=  b M..cos(o')
On pose  = o'
b = 1 ( I )
b = 1 ( II )
Si
d)(dm
< 0 alors b = 1
m( =  M.sin(')
Si
d)(dm
> 0 alors b = 1
m( = +M.sin(')
M
-M
'
m(')
90°
-90°
(I)
(II)
b = 1
b =  1
Fig. 10 : Caractéristique de m(o)
b = 1 (Fig. 17 I' )
b = 1 (Fig. 17 II' )
m(=Msin o
d'où
oo
2 
m(=+M.sino
d'où
oo
2 
180°
o
()
90°
-90°
(I')
(II')
90°
-90°
-180°
b = 1
b =  1
Fig. 11 : Caractéristique de (o)
Avantages
 Grande facilité de mise en œuvre.
 Mesures indépendantes de l'amplitude des signaux.
 Bonne sensibilité :