Corrigé de l`examen de commande par vision

ENSPS 3A ISAV – MASTER IRIV AR – Janvier 2016 1
Corrigé de l’examen de commande par vision
Durée : 1 heure. Partie à rendre sur copie séparée.
Documents autorisés.
Calculatrice autorisée. Pondération : 10 points.
Problème : robot artiste
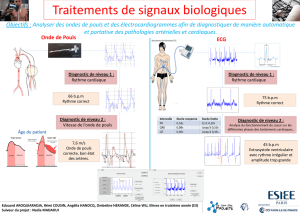
Soit le système suivant constitué d’une caméra déportée et d’un robot parallèle à câbles suspendu aux bords d’un tableau
blanc :
Caméra
Tableau
Robot
Vue de profil Vue de face
Câble Câble
Robot
Marqueur
2m
2m
Figure 1 – Robot artiste
Le point Mdu robot laisse une trace sur le tableau lorsque le robot se déplace (marqueur). Sa position cartésienne
tM= (xtyt)est définie dans le repère Rtlié au tableau. Il est matérialisé dans l’image de la caméra par une cible constituée
d’un disque noir sur fond blanc. La position (XcYc)en pixels du centre de cette cible est extraite par traitement d’image.
Le montage est tel que (XcYc) = (0 0) lorsque tM= (0 0), c’est à dire lorsque le robot est au centre du tableau (tel que
représenté sur la figure). L’orientation des axes xcet ycde l’image est définie par le repère Rclié à la caméra. La vue de
face sur la figure est celle que voit la caméra.
1. La caméra est de résolution 500 ×500 pixels. Son champ de vision couvre exactement la surface du tableau. Calculer
xtet yten fonction de Xcet Yc.
Solution : xt=Xc/500 ∗2yt=−Yc/500 ∗2
2. On souhaite faire tracer au robot un cercle de centre Met de rayon 0,5mà la vitesse de 1m/s. Donner l’équation
paramétrique définissant tM(t) = (xtyt)en fonction du temps tsachant que la position initiale du robot est
tM(0) = (0,5 0). En déduire l’équation paramétrique de (XcYc)en fonction de t.
Vitesse angulaire w : w*0.5=1 => w=2 rad/s

ENSPS 3A ISAV – MASTER IRIV AR – Janvier 2016 2
xt= 0.5∗cos(wt)yt= 0.5∗sin(wt)
Xc= 125 ∗cos(wt)Yc=−125 ∗sin(wt)
3. On utilise une connexion USB3 pour relier la caméra à l’ordinateur chargé du traitement d’image. Cette caméra est
réglée sur 100 images par secondes avec un temps d’intégration de 10ms. Elle délivre une image en noir et blanc. La
luminance de chaque pixel est codée sur 256 niveaux de gris par un octet. Calculer le temps de transfert d’une image
sachant que le débit pratique de l’USB3 est de 625 ×106octets/s.
Solution : 500 ∗500/(625.106) = 400us
4. On néglige le temps de transfert de l’image par rapport à la période d’acquisition. D’après le cours, comment se
nomme l’architecture de traitement d’image correspondante ?
Solution : "A la volée".
5. On désire asservir la position du point M dans l’image grâce à un asservissement visuel 2D de type dynamique. On
dispose d’un ordinateur très puissant sur lequel le temps de traitement d’image et le temps de calcul de la commande
sont négligeables. Pour un asservissement visuel à 100Hz et un temps d’intégration de l’image de 10ms, en déduire
la fonction de transfert en zmodélisant l’acquisition et le traitement de l’image.
Solution : (1 + z−1)/2
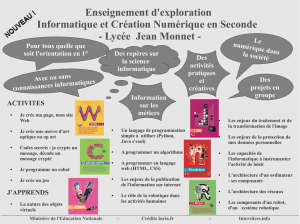
6. Le robot est approché par un intégrateur pur. On peut démontrer que la boucle de vision peut être modélisée par le
schéma-bloc de la figure 2. Calculer la fonction de transfert en boucle fermée entre (X∗
c(z)Y∗ c(z)) et (Xc(z)Yc(z))
Figure 2 – Schéma-bloc de l’asservissement visuel
en considérant que le correcteur C(z)=1.
BOZ ∗1/s -> (1 −z−1)Z(1/s2) = (1 −z−1)T z/(z−1)2=T z−1/(1 −z−1)
FTBO : T z−1/(1 −z−1)∗(1 + z−1)/2(transfo bilinéaire d’une intégrale)
FTBF : T z−1/(1 + z−1(T /2−1) + T/2z−2)
7. Pour une référence (X∗
cY∗ c)identique à celle calculée à la question 2 (équation en fonction de tdes coordonnées du
point Mdans l’image telles que le robot décrit un cercle centré en Mde rayon 0,5mà la vitesse de 1m/s), calculer
l’erreur en régime permanent de l’asservissement visuel sur le rayon (on suppose que le robot fait plusieurs tours et
que le régime permanent harmonique est atteint).
FTBF(exp(jwT))=0.1992-j0.4045
Norme = 0.45
Erreur de 55%.