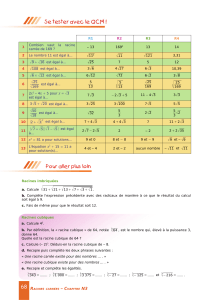
Les racines nièmes Rappel La racine carrée

Les racines nièmes

1
Rappel
La racine carrée :
Définition :
La racine carrée d'un nombre réel positif x est le nombre positif dont le carré est x.
Quelques exemples :
 la racine carrée du nombre réel 9 est 3, en effet 3 est positif et 3² = 9
 la racine carrée du nombre réel 16 est 4, en effet 4 est positif et 4² = 16
 la racine carrée du nombre réel 
 et   , en effet   est positif et 
ATTENTION !
La racine carrée n'est pas définie pour un nombre négatif, puisque le carré d'un nombre
quelconque est toujours positif.
Tout réel strictement positif admet deux racines de signes opposés
Propriétés :
 carré d'une racine carrée :  
 racine carrée d'un produit :  
 racine carrée d'un quotient : 
 racine carrée d'un carré :   
Exercices :
1) Effectue :
a)  
b) 
c)  
d) 
e)  
f)  
g)  
h) 

2
La racine cubique :
Définition :
La racine cubique d'un nombre réel positif x est le nombre positif dont le cube est x.
Quelques exemples :
 La racine cubique du nombre réel 8 est 2, en effet 2³ = 8
 La racine cubique du nombre réel 27 est 3, en effet 3³ = 27
Tableau des dix premiers cubes :
Nombre
Nombre au cube
1
1
2
8
3
27
4
64
5
125
6
216
7
343
8
512
9
729
10
1000
Petite astuce pour retrouver la racine cubique d’un réel dont la réponse est un nombre
entier :
Supposez que l’on vous donne à extraire la racine cubique de 287 496. Le dernier chiffre de ce
nombre est 6, en allant voir dans le tableau ci-dessus, on remarque que le nombre se terminant par
6 est le cube de 6, donc le dernier chiffre dans ce cas est 6. Pour déterminer le premier chiffre de la
racine cubique : supprimez les trois derniers chiffres du cube (quel que soit le nombre de chiffre le
composant) pour ne retenir que les chiffres restants. Dans cet exemple on a 287. Dans la table ci-
dessus 287 se situe entre les cubes de 6 et 7. Le plus petit de deux ces chiffres (6) correspond au
premier chiffre de la racine du nombre annoncé. La réponse est 66.
Exerce-toi !
Propriétés :
 la racine cubique d’un nombre négatif est un nombre négatif : 
Attention !
Les propriétés citées pour la racine carrée sont les mêmes pour la racine cubique !

3
Introduction
1) Complète le tableau suivant. Quelle conclusion peux-tu en tirer ?
X
0
1
|x|
X²
Conclusion :
2) Complète les tableaux suivants à l’aide de ta calculatrice et tire une conclusion :
X
X
3) À quelles conditions l’expression 
 représente-t-elle un réel ?

4
Les racines d’indice n
1. Généralisation :
Définitions :
Le nombre b est une racine nième du nombre réel a si et seulement si  
si n est pair : 
si n est impair :    
Notations et vocabulaire :
a) La racine nième de a se note 
 et a est appelé le radicand
(      )
b) 
 se lit également racine d’indice n de a (ou radical d’indice n) où n est l’indice
(      )
Propriétés :
1) Les propriétés des racines carrées sont valables pour toutes racines d’indice pair
2) Les propriétés des racines cubiques sont valables pour toutes racines d’indice
impair
Donc :
Si n est pair :
 La nième puissance d’un nombre réel est un nombre réel positif
 Aucun réel strictement négatif n’admet de racine nième
 Tout réel strictement positif admet deux racines nièmes opposées
Si n est impair :
 La nième puissance d’un nombre réel possède le même signe que ce nombre réel
 Tout nombre réel admet une seule racine nième