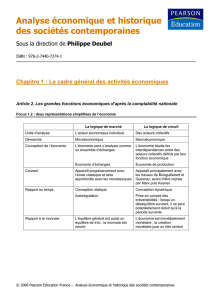
Théorie Relative de la Monnaie

Théorie Relative
de la Monnaie
version 2.0
Licence GPL V3

© Stéphane Laborde 2011 (GPL V3)
http://wiki.creationmonetaire.info
Publié en Juin 2011

Préface de Yoland Bresson
La théorie relative de la monnaie de Stéphane
Laborde s’inscrit dans la grande tradition
française de travaux de sciences économiques
produit par des ingénieurs tels ceux de Dupuit,
Cournot... jusqu’à notre seul prix Nobel de la
discipline : Maurice Allais.
Mais, toute science se construit un langage
particulier et je crains que les économistes,
comme l’honnête homme du siècle, ne saisissent
pas vraiment tout l’intérêt de cet apport
théorique sans une « traduction ».
Le « Système à Dividende Universel » que
propose l’auteur est un système monétaire dans
lequel la monnaie est uniformément distribuée
entre tous les acteurs, individus de tout âge et
de tout sexe, chacun d’eux en en recevant une
part égale.
Nous avons presque tous déjà pratiqué un tel
système… en jouant au Monopoly. En effet
chaque joueur reçoit au départ la même quantité
de monnaie, et à chaque tour par passage à la
case départ de la monnaie supplémentaire est
ajoutée, chacun percevant une même somme.
Un tour est la période de base théoriquement
3

identique pour tous, sauf que selon les aléas du
jeu, les jets de dés... le tour est fait plus ou
moins vite et que les ajouts de monnaie s’en
différencient selon les joueurs. Notez que
l’égalité des dotations monétaires n’empêche
pas l’apparition de gagnants et de perdants
selon les choix individuels et les opportunités du
hasard.
Actuellement, dans notre réalité, la répartition
de la masse monétaire ne correspond pas à un
tel système. Elle est créée et distribuée sous
forme de dette par l’intermédiaire du système
bancaire qui répond à la demande de monnaie
des particuliers en leur prêtant bien plus de
monnaie qu’elles ne détiennent elles-mêmes
contre un intérêt supérieur à celui qu’elles-
mêmes doivent supporter en s’approvisionnant
auprès de la Banque Centrale, émettrice en
premier et dernier ressort. Le pays dispose ainsi
d’une masse monétaire dite M3.
Il faut bien distinguer la masse monétaire,
stock de monnaie disponible, comme
éternellement présent, fixe sauf création
monétaire supplémentaire, des flux de revenus
en monnaie que captent les individus dans
l’activité économiques et les échanges : la masse
monétaire engendre des flux de revenus dont la
somme sur l’année est traditionnellement
évaluée comme le PIB. Ce lien qui paraît trivial
est en vérité très subtil comme nous le verrons
plus loin.
4

Dès lors l’auteur cherche à répondre à la
question suivante : Quelle règle de création
monétaire doit-on adopter, et à quelle rythme
faut-il accroître la masse monétaire, de façon à
instituer un système à Dividende Universel, tel
que sa densité, c'est-à-dire sa répartition selon
les individus, soit uniforme dans l’espace et dans
le temps ?
Il suppose une population stable en nombre
avec une espérance de vie donnée. C'est-à-dire
qu’il admet un solde démographique naturel nul :
il y a autant de naissances que de décès et pas
de migrations. L’espérance de vie correspond
alors à la durée au bout de laquelle il n’y a plus
aucun ancien vivant. La population est
totalement renouvelée depuis la mise en place
de la nouvelle règle ; la densité est maintenant
pour tous uniforme qu’elle que soit celle qui
prévalait à l’origine. Le Système à Dividende
Universel, celui rappelons-le où chacun reçoit
une part égale de la masse monétaire est
complètement réalisé.
La réponse est ce que l’auteur appelle le
« Dividende Universel Optimal » : la masse
monétaire doit annuellement croître d’un facteur
« c », évidemment inversement proportionnel à
l’espérance de vie- c'est-à-dire à la durée de
renouvellement de la population ou à celle de la
mise en place complète du système - et ce
surplus de monnaie doit être également et
inconditionnellement distribué entre tous les
membres de la population. Ce facteur c est égal
5