Oscillations dans le circuit RLC série (Correction)

Physique – Terminale S
Chapitre 8
Travaux Pratiques n°8
Le dipôle RLC série - Correction
Oscillations dans le circuit RLC série (Correction)
1 – DECHARGE D’UN CONDENSATEUR A TRAVERS UNE BOBINE REELLE OU DANS UN CIRCUIT RLC SERIE
1.1 – Montage
Nom du fichier : « RLC_decharge »
1. Montrer, sur ce schéma, comment acquérir uC et uR.
On acquiert UR par la voie EA0 et UC par la voie EA1, en convention récepteur.
2. Que se passe-t-il lorsque l’interrupteur est en 1 ?
En basculant K sur la position 1, le générateur est relié aux bornes du condensateur : on charge le
condensateur.
3. Que se passe-t-il lorsque l’interrupteur est en 2 ?
En basculant K sur la position 2, on décharge le condensateur dans la bobine et le conducteur ohmique en
série.
4. Mesurer L pour 500 spires et 250 spires avec l’inductancemètre et r de la bobine dans chaque cas.
Pour 500 spires : L = 11,0 mH et r = 9,8 Ω.
Pour 250 spires : L = 2,5 mH et r = 4,8 Ω.
5. On veut étudier la décharge du condensateur donc on déclenche lorsque l’interrupteur passe de 1 de 2.
Déterminer les conditions initiales (tensions, intensités) de cette étude.
Initialement, le condensateur est chargé (position 1) : la tension à ses bornes uC est donc maximale (uC = E).
L’intensité dans le circuit est initialement nulle (le circuit est ouvert le temps qu’on bascule de 1 à 2) : la
tension uR est donc initialement nulle ; en revanche, puisque le courant s’établit,
0
0
t
di
dt 
  et la tension uL
aux bornes de la bobine n’est pas nulle (sa composante résistive « r × I » est toutefois nulle).
1.2 – Observation de uC
Réglages : E = 6,0 V, bobine de 500 spires, C = 2 F, R = 2 .
1. Tracer uC = f(t) dans la fenêtre 2.  Courbe n°1.2
2. Comment varie l’amplitude de uC dans le temps ? Justifier le terme de « pseudo-période ».
La courbe représentative de uC(t) présente des oscillations amorties : on pourrait parler d’un évolution
périodique s’il n’y avait pas d’amortissement, mais il convient de parler d’une évolution « pseudo-
périodique ».
3. Mesurer 5 pseudo-périodes afin de déterminer la pseudo-période. Quel est l’intérêt de cette méthode ?
On mesure, pour 5 pseudo-périodes, Δt = 4,603 ms. On en déduit T = 4,603 / 5 = 0,9206 ms. On aurait pu ne
mesurer qu’une pseudo-période… mais l’intérêt d’en mesurer 5 est d’augmenter la précision, en faisant une
sorte de moyenne sur une durée plus grande (donc mesurée avec moins d’incertitude relative).
1.3 – Observation de l’intensité dans le circuit
1. Déterminer l’expression de l’intensité dans le circuit.
Régler les paramètres d’acquisition
suivant dans le logiciel
LATIS PRO :
Nombre de points : 1000 points, Total temps : 5 ms.
Déclenchement : source : uR; sens : montant et seuil : 0,05 V.
C
L, r
R
E
+
1
2
K
EA0
EA1
Les courbes sont en annexe

Physique – Terminale S
Chapitre 8
Travaux Pratiques n°8
Le dipôle RLC série - Correction
( )
( ) R
U t
i t
R
2. Tracer i = f(t) dans la fenêtre 3.  Courbe n°1.3
3. Comment varie i par rapport à t ? Conclure.
L’intensité i(t) est une grandeur oscillante et amortie dans le temps.
1.4 – Observation de la charge des armatures du condensateur
1. Déterminer l’expression de la charge en fonction de uC.
( ) ( )
C
q t C U t
2. Tracer q = f(t) dans la fenêtre 4.  Courbe n°1.4
3. Comment varie q par rapport à t ? Conclure.
La charge q(t) du condensateur est une grandeur oscillante et amortie dans le temps.
4. Que dire de la charge lorsque i est maximale et lorsque i est nulle ?
Lorsqu’on regarde les courbes i(t) et q(t), on peut se rendre compte que lorsque i est maximale, q est nulle, et
lorsque i est nulle, q est extrémale (minimale ou maximale, mais maximale en valeur absolue).
2 – INFLUENCE DES PARAMETRES DU CIRCUIT
2.1 – Influence de la capacité du condensateur (fichier RLC_influ_C.ltp)
On a tracé uC = f(t) avec C1≈1F, C2≈ 2 µF, C5≈ 5 µF et C10 ≈10 F. Pour ces mesures, L = 40 mH.
1. Sur quoi influe la capacité du condensateur ?
La capacité C du condensateur influe sur la valeur de la pseudo-période T : plus C est grande, plus la pseudo-
période est grande.
Remarque : les courbes uC(t) ne démarrent pas toutes de la valeur uC,max = E = 6,0 V. Ceci s’explique par la
durée entre le début de l’acquisition et la bascule de l’interrupteur, le condensateur commençant à se
décharger entre temps… Ceci n’influe toutefois pas du tout sur la valeur des pseudo-périodes obtenues.
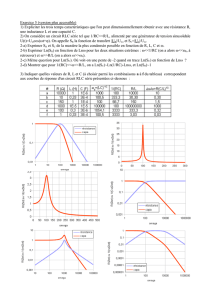
2. Déterminer les pseudo-périodes dans les quatre 4 cas, T1, T2, T5 et T10. Justifier votre méthode.
C (µF) 1,02 2,02 5,25 10,47
T (ms) 1,37 1,85 2,90 4,10
C
(µF½) 1,01 1,42 2,29 3,24
Pour chaque valeur de T, on détermine la durée de plusieurs pseudo-périodes, comme nous avons procédé au
1.2.
3. Tracer T = f(C)  Courbe n°2.1a et T = f( C)  Courbe n°2.1b. Conclure.
La courbe T = f(L) ne correspond à aucune fonction simple, mais ressemble à une racine carrée : en traçant T
= f( C), on voit apparaître une relation linéaire,
T = 1,2753 × C
2.2 – Influence de l’inductance de la bobine (fichier RLC_influ_L.ltp)
On a tracé uC = f(t) avec une bobine de L10 ≈ 10 mH, L40 ≈ 40 mH, L70 ≈ 70 mH et L90 ≈ 90 mH. Pour ces
mesures, C = 10,5 µF.
1. Sur quoi influe l’inductance de la bobine ?
L’inductance L de la bobine influe sur la valeur de la pseudo-période T : plus L est grande, plus la pseudo-
période est grande.
2. Déterminer les pseudo-périodes dans les quatre cas, T10, T40, T70 et T90. Justifier votre méthode.
L (mH) 11,1 40,0 71,3 93,7
T (ms) 2,15 4,09 5,00 6,27
L
(mH-½) 3,33 6,23 8,44 9,68

Physique – Terminale S
Chapitre 8
Travaux Pratiques n°8
Le dipôle RLC série - Correction
Pour chaque valeur de T, on détermine la durée de plusieurs pseudo-périodes, comme nous avons procédé au
1.2.
3. Tracer T = f(L)  Courbe n°2.2a et T = f( L)  Courbe n°2.2b. Conclure.
La courbe T = f(L) ne correspond à aucune fonction simple, mais ressemble à une racine carrée : en traçant T
= f( L), on voit apparaître une relation linéaire,
T = 0,0205 × L
Détermination de l’expression de la pseudo-période
1. Déduire des questions 2.1 et 2.2 précédentes que la pseudo-période peut s’écrire sous la forme
T k L C
, k étant une constante.
Résumons. Nous avons déterminé les relations empiriques
T = 1,2753 × C avec L = 40,0 mH
T = 0,0205 × L avec C = 10,47 µF
On peut synthétiser ces résultats sous la forme
T k L C
2. Montrer que k n’a pas de dimension, par analyse dimensionnelle, et qu’elle s’exprime simplement en
fonction du nombre π.
2
/ / ( / ) /
U q q q
L C L C t
di dt U di dt q t t
        donc
L C t
Ainsi,
t
T
kt
L C
  .
T = 1,2753 × C avec L = 40,0 mH conduit à
1, 2753
k L  soit 3
1, 2753 1, 2753
6,38
40,0.10
kL
T = 0,0205 × L avec C = 10,47 µF conduit à
0,0205
k C  soit 6
0,0205 0,0205
6,34
10,47.10
kL
On peut donc conjecturer que 2k .
Ainsi,
2
T L C
NB : si nous n’avions pas fait de régressions linéaires en 2.1 et 2.2, il suffit de prendre quelques couples de
valeurs (T,L) et/ou (T,C).
2.3 – Influence de la résistance du circuit
a) Si R est faible
1. Tracer uC = f(t) avec une résistance de 2 et de 20 dans la fenêtre 4 sans changer les autres paramètres.
Ne pas oublier de légender  Courbe n°2.3a
2. Sur quoi influe la résistance du circuit ?
La résistance R du circuit influe sur l’amortissement des oscillations : plus R est grand, plus les oscillations
s’amortissent rapidement.
b) Si R est grand
1. Tracer uC = f(t) avec une résistance de 50  et de 90 dans la fenêtre 4 sans changer les autres paramètres
du circuit.  Courbe n°2.3b
2. Comment qualifier le régime de fonctionnement du circuit RLC série lorsque R est grand ?
Le régime de fonctionnement du circuit RLC, pseudo-périodique si R est petit, tend à devenir apériodique
lorsque R est grand.
NB :
3
6
11,0.10
2 2 148
2,00.10
c
L
RC
c) Si R était nulle

Physique – Terminale S
Chapitre 8
Travaux Pratiques n°8
Le dipôle RLC série - Correction
1. Prévoir ce qu’il se passerait si RT était nulle. Schématiser uC = f(t) dans ce cas.
Si R était nul, les oscillations ne seraient pas amorties : le régime de fonctionnement serait alors purement
périodique.
2. Comment appellerait-on ce genre de circuit ?
Le circuit RLC serait alors un circuit oscillant périodique non amorti.
4 – ETUDE ENERGETIQUE DU CIRCUIT RLC SERIE :
Nom du fichier : RLC_energie ».
Acquérir uC = f(t) et uR = f(t) comme dans le I.
1. Déterminer les expressions des énergies emmagasinées par le condensateur EC et par la bobine EL ainsi que
l’énergie totale du système condensateur-bobine, qu’on notera E.
2. Tracer EC = f(t) et EL = f(t) dans la fenêtre 2  Courbe n°4.2. Comment varie EC et EL?
EC et EL oscillent à la manière de UC(t) et de i(t), mais en restant positives (présence du carré dans leurs
expressions). Par ailleurs, les variations sont en opposition de phase : lorsque EC est maximale, EL est
minimale, et réciproquement.
3. Tracer EC = f(t), EL = f(t) et E = f(t) dans la fenêtre 3  Courbe n°4.3 . Comment varie E ?
L’énergie totale E = EC + EL décroît, à la manière des oscillations observées dans UC(t) et i(t). L’énergie totale
du circuit diminue au cours du temps.
4. A quoi est due la diminution de l’énergie totale du système au cours du temps ?
C’est dans l’amortissement des oscillations qu’il faut chercher la diminution d’énergie : la présence de R
implique une dissipation de l’énergie par effet Joule ; cette énergie dissipée est transmise à l’environnement
sous forme d’énergie thermique au niveau de la résistance (bobine et conducteur ohmique).
5. Comment serait l’énergie totale si RT était nulle ?
Dans le cas où R est nulle, les oscillations ne seraient plus amorties : l’énergie totale serait constante.
6. Représenter EC = f(t), EL = f(t) et E = f(t) dans ce cas.
5 – BILAN DE CE TP
Le dipôle RLC série constitue est le siège d’oscillations électriques pour peu que la résistance totale du circuit
soit suffisamment faible ; dès lors, la pseudopériode To des oscillations amorties est fonction des paramètres du
dipôle,
2
o
T L C

Physique – Terminale S
Chapitre 8
Travaux Pratiques n°8
Le dipôle RLC série - Correction
Ce TP permet de constater expérimentalement le principe de fonctionnement d’un tel dispositif : le
condensateur initialement chargé se décharge dans la bobine ; cette dernière lui répond en intensité et le
recharge en inversant le signe de ses armatures, et ainsi de suite… jusqu’à ce que la dissipation intervenant par
effet Joule au niveau de la résistance « à chaque échange » annule totalement l’énergie initiale stockée dans le
condensateur. Cette dissipation serait en théorie nulle dans un circuit où la résistance serait négligeable.
Les élèves de spécialité le savent : le RLC série constitue un filtre passe-bande passif très simple permettant
d’éliminer une bande de fréquences donnée dans un signal. La largeur de bande est évidemment commandée
par les paramètres physiques des composants R, L et C qui sont utilisés. Il permet alors, par exemple, de
sélectionner la fréquence captée par un récepteur d’ondes radio…