note sur la modelisation du risque d`inflation

Note Modélisation Risque Inflation
Infra Finances – SARL au capital de 120 000 € - RCS de Paris 504 510 405
Adresse : 23, avenue Foch – 75116 Paris – Tél. : [phone]
Courriel : [e-mail] – Site : www.infrafinances.com Page | 1
NOTE SUR LA MODELISATION DU RISQUE D’INFLATION
1/ RESUME DE L’ANALYSE
Cette étude a pour objectif de modéliser l’écart entre deux indices d’inflation afin
d’appréhender le risque à très long terme qui serait pris par un opérateur économique qui
aurait un coût de production lié à un indice et un chiffre d’affaire lié à un autre indice.
Nous retrouvons ce type de risque dans le cas des partenariats publics-privés où le
titulaire du contrat reçoit une redevance indexée sur un indice ou un ensemble d’indices mais peut,
sur une période longue, avoir des coûts de production qui ne sont pas corrélés aux indices de
référence du contrat.
A partir de chroniques à très long terme (depuis 1956) de l’indice général des prix à la
consommation (IC) et de l’indice du coût de construction (ICC), nous démontrons que l’écart entre
ces deux indices suit une loi normale de moyenne 0,34 et d’écart-type 2,6. Nous utilisons la méthode
de Monte-Carlo pour simuler le risque d’écart entre deux indices d’inflation et estimer la
valorisation du risque d’indexation en fonction de la maturité du contrat. Nous calculons qu’un
opérateur économique demanderait un montant supplémentaire de 9% en Valeur Actuelle Nette pour
augmenter la maturité du contrat de 7 à 20 ans.
2/ ANALYSE GRAPHIQUE DES SERIES LONGUES D’INFLATION ET
FORMALISATION DU PROBLEME
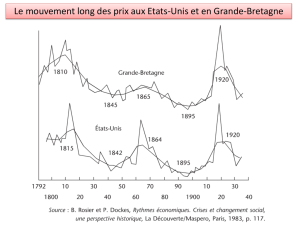
La courbe de superposition des 2 jeux de données montre une corrélation des 2 données sur
l’ensemble de la période en se basant sur l’allure de la courbe. On peut voir une nette augmentation
au-delà des 10% des 2 taux qui sont quasiment superposés notamment lors des chocs pétroliers de
1973 et 1979 (qui ne sont ressentis que 2 à 3 ans après en France). On constate néanmoins que
l’impact de l’inflation sur l’indice ICC n’est pas le même d’une année sur l’autre. C’est cette différence
d’impact qui nous intéresse et qu’il convient d’étudier.
Tableau 1 : Graphique superposé (ICC et Inflation)
Tableau 2 : Graphique évolution écart

Note Modélisation Risque Inflation
Infra Finances – SARL au capital de 120 000 € - RCS de Paris 504 510 405
Adresse : 23, avenue Foch – 75116 Paris – Tél. : [phone]
Courriel : [e-mail] – Site : www.infrafinances.com Page | 2
Nous modélisons ε correspondant à l’équation : ε = ICC – Inflation
Après avoir rassemblé des jeux de données en nombre suffisant, l’intérêt a été de voir d’un
point de vue statistique comment la variable aléatoire ε se comportait. A partir de l’ensemble des
observations entre 1956 et 2009, nous obtenons la moyenne et l’écart-type de ε. En classant les
données par ordre croissant (en partant donc du minimum de la série), on obtient la fonction de
répartition de la série ICC-Inflation.
Tableau 3 : Statistiques et fonction de répartition
STATISTIQUES
Nbr Observation 54,00
Moyenne 0,34
Min -5,93
Max 8,29
Ecart-type 2,586
Max-Min 14,22
3/ MODELISATION MATHEMATIQUE
Nous effectuons un test de Khi-2, appelé « Goodness of fit Test » (test qui permet de
valider la modélisation d’une variable aléatoire par une loi de probabilité connue). Cette analyse
distribue les données de la série en fractiles (plusieurs intervalles). Ainsi chaque intervalle a une
probabilité d’apparition et on peut obtenir la courbe de densité de probabilité. A partir des données
obtenues, on peut valider ou non l’hypothèse selon laquelle la variable aléatoire étudiée est
modélisable par une loi normale.
Dans le cas présent, pour l’étude d’ICC-Inflation, l’hypothèse est validée selon le test de Khi-2.
Nous avions divisé l’intervalle de l’échantillon en 12 fractiles pour arriver à un résultat visible
graphiquement. L’outil permet une comparaison entre l’échantillon, la densité de probabilité de la loi
normale pour l’échantillon donnée et la densité de probabilité de la loi de Gumble. Graphiquement le
résultat est le suivant :

Note Modélisation Risque Inflation
Infra Finances – SARL au capital de 120 000 € - RCS de Paris 504 510 405
Adresse : 23, avenue Foch – 75116 Paris – Tél. : [phone]
Courriel : [e-mail] – Site : www.infrafinances.com Page | 3
Tableau 4 : Vue de l’outil d’analyse et de modélisation
Tableau 5 : Graphe de comparaison
 On note donc que la densité de probabilité de l’échantillon est plus proche de celle de
la loi normale en termes de rapprochement. De plus, l’outil d’analyse valide l’hypothèse
selon laquelle ε est modélisable par une loi normale car le Chi-Square calculé est inférieur
au Chi-Square donné par la table standard du Khi-2 pour un seuil d’erreur de 5%.
 De plus une autre bonne indication est le coefficient de détermination R² qui est calculé par
simulation de Monte-Carlo. On obtient une valeur légèrement supérieure à 1 due à la
précision de la simulation. Par extension, on dit donc que R² ~ 1. Ce qui confirme que le
modèle statistique et probabiliste choisi est valable et que la variable aléatoire ε est
modélisable par une loi normale.

Note Modélisation Risque Inflation
Infra Finances – SARL au capital de 120 000 € - RCS de Paris 504 510 405
Adresse : 23, avenue Foch – 75116 Paris – Tél. : [phone]
Courriel : [e-mail] – Site : www.infrafinances.com Page | 4
4/ QUANTIFICATION DU RISQUE D’INFLATION
A l’aide d’autres chroniques, notamment les indices nationaux des prix du bâtiment et de la
construction (indices BT01 sur 23 ans et indices BT50 sur 17 ans), nous avons réalisé une autre étude
statistique de la même manière que l’étude ICC-Inflation :
Tableau 6 : Moyennes et écart-types sur d’autres exemples de risques d’inflation
Nous constatons que les moyennes historiques des 4 premières comparaisons (taux BT01 et
BT50 avec le taux d’inflation et le taux d’indice des coûts de construction) sont supérieures à la
moyenne que l’on a trouvé dans l’étude précédente. Leurs écart-types respectifs sont quant à eux
inférieurs à la série à long terme ICC-Inflation que nous avons étudié.
Nous utilisons la méthode de Monte-Carlo en simulant l’impact de la variable aléatoire
correspondant au risque d’indexation en utilisant la méthode suivante :
 Etape 1 : (pour une estimation du risque d’indexation à 20 ans par exemple)
Tirage aléatoire de 20 variables suivant une loi normale de moyenne 0,34 et d’écart-type 2,6
pour simuler le risque annuel entre l’année 1 et l’année 20.
 Etape 2 : Actualisation des 20 estimations annuelles futures du risque au taux de 4% pour
calculer la valeur actuelle nette (VAN).
 Etape 3 : Utilisation de la méthode de Monte-Carlo (avec 10,000 itérations) qui va calculer la
VAN moyenne Standard, la VAN moyenne valeurs positives, la VAR 95% standard et la VAR
95% valeurs positives.
Tableau 7 : Vue de la simulation réalisée
Taux d'actualisation 4%
Nombre de simulations 10 000
Paramètres Loi normale
Mu (Moyenne) 0,34%
Sigma (Ecart-type) 2,59%
7 ans 20 ans
VAN moyenne standard 1,89% 4,66%
VAN moyenne valeurs positives 7,21% 16,49%
VAR95% standard 11,67% 17,63%
VAR95% valeurs positives 13,94% 25,10%
LANCER Simulation de Monte-Carlo

Note Modélisation Risque Inflation
Infra Finances – SARL au capital de 120 000 € - RCS de Paris 504 510 405
Adresse : 23, avenue Foch – 75116 Paris – Tél. : [phone]
Courriel : [e-mail] – Site : www.infrafinances.com Page | 5
Nous avons démontré que l’écart entre deux indices d’inflation était une variable aléatoire qui
suivait une loi normale. Cet écart futur est un estimateur du risque pris par un opérateur économique
qui aurait signé un contrat de prestation de service indexé sur un indice défini contractuellement à
l’avance mais dont les coûts de production pourraient varier en fonction d’un autre indice.
A partir des données de taux d’actualisation, du nombre de simulations (itérations pour Monte-
Carlo), et des paramètres de la loi normale, le programme simule sur 7 ou 20 ans des estimations
des écarts annuels futurs entre deux indices d’inflation et actualise ces séries d’écarts afin de
mesurer la différence de risque entre un contrat de service à 7 ans et un contrat de service à 20 ans
pour calculer la valeur actuelle nette des risques futurs.
On distingue la VAN « standard » de la VAN « valeurs positives » :
 Dans le cas « standard », toutes les variables aléatoires simulées sont prises en compte
dans le calcul de la VAN : nous estimons dans ce cas que l’opérateur économique
demanderait un montant supplémentaire de 2,77% (4,66% : VAN du risque à 20 ans –
1,89% : VAN du risque à 7 ans) pour augmenter la maturité du contrat de 7 à 20 ans.
 Dans le cas « valeurs positives », seules les variables aléatoires positives sont prises en
compte dans le calcul de la VAN. Il est donc logique de trouver une VAN moyenne plus
élevée dans ce cas : dans ce cas l’opérateur économique demanderait un montant
supplémentaire de 9,28% (16,49% : VAN des valeurs positives à 20 ans – 7,21% : VAN
des valeurs positives à 7 ans) pour augmenter la maturité du contrat de 7 à 20 ans.
Nous estimons donc qu’un opérateur économique demanderait un prix supplémentaire afin de se
protéger contre le risque d’indexation de 9,3% s’il ne tenait compte que du risque de perte
(moyenne des cas de perte où l’indexation de ses coûts de production est supérieure à l’indexation
de son chiffre d’affaires) ou de 6% qui représente le risque supplémentaire dans tous les cas de
figure avec une probabilité d’occurrence de 95%.