DS n°3 : optique et niveaux d`énergie

1S Correction du DS n°3
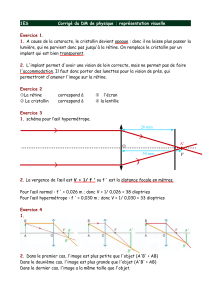
n 1) Pour être perçue comme nette, l’image doit se former sur la rétine.
2) La relation de Descartes s’écrit : 111
'
OA' OA f
−=
.
L’objet est à l’infini donc OA →−∞ ce qui donne 10
OA →.
Dans la relation de Descartes : 11
'
OA' f
=.
Donc la distance à laquelle doit se former l’image (OA’) est égale à la
distance focale f ’.
3) D’après la question 1) l’image doit se former sur la rétine donc à 16,7 mm
de la « lentille ». Donc OA’ = f’ = 16,7 mm.
Par définition de la vergence : -3
159,9
16,7.10
C==
La vergence de l’œil normal au repos vaut 59,9 δ
4)
5) Maintenant on a OA 0,5m=− puisque l’œil doit percevoir une image nette
qui se forme toujours sur la rétine.
3
11 1 1
0,5
OA' OA 16,7.10 -
C−
=−= −= 61,9 δ
La vergence de l’œil qui accommode pour observer un objet placé à 50 cm
est égale à 62 dioptries.
6) Ici C = 63 δ ; et OA' =16,7 mm.
3
11 1 63
OA OA' 16,7.10
C−
=−= − = -3,1 m-1.
1
OA 3,1 =
−= - 0,32 m, soir 32 cm.
Donc l’objet est placé à 32 cm de l’œil.
o Le spectre solaire
1) Pour λ < 400 nm : Ultraviolets ; pour 400 nm < λ < 800 nm : visible ;
pour λ > 800 nm : infrarouges.
2) Le maximum d’intensité lumineuse est atteint pour λmax = 480 nm.
La loi de Wien permet alors de calculer : 33
9
max
2,89.10 2,89.10
480.10
T
λ
−
−
−
== = 6021 K
qui devrait s’écrire 6,02.103 K avec 3 C.S.
3) – Le fond continu du spectre solaire est dû à la présence de gaz chauds qui
produisent l’émission d’un spectre continu d’origine thermique analogue à
l’émission d’un corps noir.
- Les raies noires sont dues à la présence d’entités (atomes, ions) dans la
chromosphère qui reçoivent la lumière blanche et qui absorbent certaines
radiations.
4) Ces raies noires permettent de connaître la composition chimique du
Soleil.
5)
c d e f g
434 nm 486 nm 518 nm 589 nm 656 nm
H ou Cr H Mg Na H
Un atome peut être caractérisé par ses raies d’émission ou d’absorption.
Comme ses niveaux d’énergie sont quantifiés et sont propres à chaque type
d’atome, les raies d’absorption ou d’émission permettent d’identifier un
atome.
A
B
Rétine
Cristallin B’
300 400 500 600 700 λ (nm)
intensité
lumineuse
λ
max

p La nébuleuse d’Orion
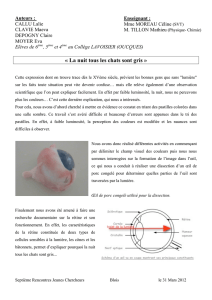
1) Il y a émission puisque l’atome effectue
une transition d’un niveau d’énergie
(E2 = - 1,51 eV) vers un niveau inférieur
(E1 = - 3,4 eV).
2)
3) La relation de Planck s’écrit :
hc
E
λ
Δ= donc
34 8
19
6,63.10 3.10
(1,513,4)1,6.10
hc
E
λ
−
−
×
==
Δ−+ × = 6,58.10-7 m
λ = 658 nm.
4) C’est une radiation rouge- orangé (voir photo de la nébuleuse ci-dessus).
5a et b)
6 a) Ces particules sont appelées photons.
6 b) Chaque photon transporte une énergie donnée par la relation : Eh
ν
=.
Donc E = 6,63.10-34 × 3,64.1014 = 2,41.10-19 J.
6 c) L’énergie de chaque photon vaut 19
19
2,41.10
1, 6. 10
−
−= 1,51 eV.
La seule transition possible est alors E 2 → E ∞ .
6 d) L’énergie totale du flash vaut 1,208.10-13 J et chaque photon emporte
2,41.10-19 J. On aura donc 13
19
1,208.10
2,41.10
−
−= 5,01.105 photons susceptibles
d’ioniser autant d’atomes d’hydrogène. (3 C.S. dans le résultat puisque la
fréquence ν = 3,64.1014 Hz qui a servi à calculer l’énergie de chaque photon
en comportait 3).
E 2
E 1
Ionisation
Niveau
fondamental