initialement-1

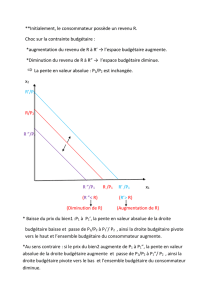
**Initialement, le consommateur possède un revenu R.
Choc sur la contrainte budgétaire :
*augmentation du revenu de R à R’ → l’espace budgétaire augmente.
*Diminution du revenu de R à R” → l’espace budgétaire diminue.
La pente en valeur absolue : P1/P2 est inchangée.
x2
R’/P2
R/P2
R ”/P2
R ”/P1 R /P1 R’ /P1 x1
(R ”˂ R) (R’˃ R)
(Diminution de R) (Augmentation de R)
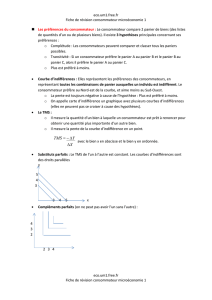
* Baisse du prix du bien1 :P1 à P1’, la pente en valeur absolue de la droite
budgétaire baisse et passe de P1/P2 à P1’/ P2 , ainsi la droite budgétaire pivote
vers le haut et l’ensemble budgétaire du consommateur augmente.
*Au sens contraire : si le prix du bien2 augmente de P1 à P1”, la pente en valeur
absolue de la droite budgétaire augmente et passe de P1/P2 à P1”/ P2 , ainsi la
droite budgétaire pivote vers le bas et l’ensemble budgétaire du consommateur
diminue.

x2
R/P2
R/P1” R/P1 R/P1’ x1
1.2-Résolution du programme du consommateur :
A -la maximisation de l’utilité sous la contrainte du budget :
Le consommateur cherche à maximiser son utilité sous la contrainte de son
revenu. Ce choix de consommation peut être analysé de manière graphique mais
aussi de manière algébrique.
1.2.1-La résolution graphique :
*Pour atteindre le maximum d’utilité sous la contrainte de son revenu, le
consommateur doit choisir un panier qui se situe sur la courbe d’indifférence la
plus élevée possible et sur sa droite de budget (puisqu’il dépense tout son
revenu.).

x2
x’1 E
U¨
U’
U
x’2 x2
**Le panier E procure au consommateur un maximum d’utilité dans le respect
de sa contrainte budgétaire (CB). E est donc le panier optimal.
**En valeur absolue, la pente de la tangente en valeur absolue à la courbe
d’indifférence (C.I) est égale au TMS.
**la pente de la droite du budget est égale au rapport des prix.
**A l’équilibre, (au point E, panier optimal) , il y a égalité entre le TMS et le
rapport des prix des biens.
**A l’équilibre, on a donc égalité entre les utilités marginales pondérées par
tous les prix pour tous les biens.
TMS =Um1(x1, x2) /Um2(x1, x2) = P1/P2
Um1(x1, x2) / P2 = Um2(x1, x2) / P1

1.2.2- Résolution algébrique :
Max U(x1, x2)
x1, x2
Sous contrainte budgétaire (s.c) : P1.x1+P2.x2 = R
**Il y a deux méthodes pour résoudre ce programme :
1. la méthode de substitution.
2. La méthode du Lagrangien.
** Méthode par substitution**
La contrainte budgétaire est : P1.x1+P2.x2 = R
On exprime x2 en fonction de x1 :
x2= (- P1 / P2). x1 + R/ P2
On remplace x2 par son expression dans la fonction d’utilité :
U( x1 , x2(x1) ) = U( x1 , R/ P2 – (P1 / P2). x1 )
On maximise,
Max U( x1 , R/ P2 – (P1 / P2). x1)
X1 X2
On atteint l’optimum lorsque la différentielle totale de U par rapport à x1 est
nulle.
dU/ dx1 = ƏU/ Ə x1 + ƏU /Ə x2. dx2/ dx1 =0
(On a : d U= ƏU/ Ə x1.dx1 + ƏU /Ə x2. dx2)
dx2/ d x1 = - P1 / P2 (car : x2= (- P1 / P2). x1 + R/P2 )

 Retrouve bien que les valeurs d’équilibre (x1*, x2*)
(ƏU(x1*, x2*)/Ə x1) / (ƏU(x1*, x2*)/ Ə x2) = P1 / P2
→ Um1(x1*, x2*)/Um2(x1*, x2*)= P1 / P2
** Méthode de Lagrangien** :
La fonction de Lagrange, dite Lagrangienne s’écrit :
L(x1,x2, λ)= U(x1, x2)+ λ( R-P1.x1-P2. x2) ( λ ≠0)
Où λ est appelé ^^ multiplicateur de Lagrange^^
 Le théorème de Lagrange indique que les valeurs optimales de : x1 et
x2 respectent les trois conditions du premier ordre :
 ƏL(x1, x2, λ)/ Ə x1=0
 ƏL(x1, x2, λ)/ Ə x2=0
 ƏL(x1, x2, λ)/ Ə λ=0
ƏU(x1, x2)/ Ə x1 – λP1=0 (1)
ƏU(x1, x2)/ Ə x2 – λP2=0 (2)
R - P1.x1 – P2.x2 =0 (3)
(1)/(2) (ƏU(x1, x2)/ Ə x1) / (ƏU(x1, x2)/ Ə x2) = P1 /P2
Um1(x1, x2) /Um2(x1, x2) = P1 /P2 (4)
Nous retrouvons donc le résultat précédent selon lequel le panier du
bien optimale est caractérisé par l’égalité entre le TMS et le rapport
des prix des biens.
La troisième condition du premier ordre (3) assure que le
consommateur sature sa contrainte de budget.