Chapitre n°8 : « Parallélogrammes particuliers »

5ème4 2009-2010
Chapitre n°8 : « Parallélogrammes particuliers »
Chapitre n°8 : « Parallélogrammes particuliers »
I. Rappels
Définition
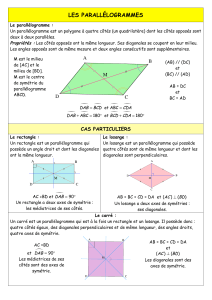
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Construction au compas
Propriétés
Dans un parallélogramme :
•les côtés opposés sont de même longueur ;
•les diagonales se coupent en leur milieu ;
•les angles opposés sont de même mesure ;
•les angles consécutifs sont supplémentaires.
II. Rectangle
Définition
Un rectangle est un quadrilatère qui possède quatre angles droits.
Illustration
On remarque qu'il a suffit de faire trois angles droits.

5ème4 2009-2010
Propriétés
On a les propriétés communes à tous les parallélogrammes :
•les côtés opposés sont de même longueur ; les diagonales se coupent en leur milieu.
Et la propriété qu'on a seulement pour les rectangles :
•les diagonales sont de même longueur.
Exemple
JHYU
est un rectangle de centre
G
. Fais une figure à main levée et indique toutes les
longueurs égales. Code la figure.
On a :
•
JH =UY
;
JU =HY
;
•
GJ =GH =GY =GU
;
•
JY =UH
.
Propriétés réciproques (en partant du parallélogramme)
•Si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle.
•Si un parallélogramme possède un angle droit alors c'est un rectangle.
Exemple 1
On considère le parallélogramme
IJKL
codé ci-contre.
Que peut- on dire ? Démontre-le.
On peut dire que
IJKL
est en fait un rectangle. En
effet, on sait que si un parallélogramme a ses
diagonales de même longueur alors c'est un rectangle.
Or sur la figure, le codage indique que
OI =OJ =OK =OL
, c'est à dire que
LJ =IK
.
D'où la justification.
Exemple 2
On suppose que
THGY
est un parallélogramme tel que
THG=90°
.
Fais une figure à main levée. Que peut-on dire ?
Démontre-le !

5ème4 2009-2010
Rédiger une démonstration (méthode à connaître !)
Il y a trois points à respecter dans toute démonstration.
•1 ère étape : « On donne la propriété, la définition ou un théorème utile pour
répondre au problème »
Si un parallélogramme possède un angle droit alors c'est un rectangle.
•2ème étape : « On donne les éléments de l'énoncé ou du codage qui permettent
d'utiliser la propriété donnée avant ».
D'après l'énoncé, on sait que
THGY
est un parallélogramme. D'après le codage, on
sait que
THG=90°
.
•3ème étape : « On conclut »
Donc
THGY
est un rectangle.
Axes et centre de symétries
•Il y a deux axes de symétrie :
ils passent par les milieux des
côtés (droites en rouge)
•Il y a un centre de symétrie :
c'est le point
I
, centre du
rectangle.
III. Losange
Définition
Un losange est un quadrilatère qui a ses quatre côtés de même longueur.
Illustration
On commence par tracer deux demi-droites de même
origine.
On choisit un écartement à l'aide du compas. Cela
permet de construire quatre côtés de même longueur.

5ème4 2009-2010
Propriétés
Les propriétés communes aux parallélogrammes :
•les côtés opposés sont parallèles ; les diagonales se coupent en leur milieu.
La propriété qui est propre aux losanges :
•les diagonales sont perpendiculaires .
Exemple
On considère un losange
UHYT
. Fais une figure à main levée. Code la figure puis donne les
longueurs égales et les droites perpendiculaires.
On a :
UT =TY =YH =UH
;
UO=OY
;
OT =OH
UY 
est perpendiculaire à
TH 
Propriété réciproque (en partant du parallélogramme)
•Si un parallélogramme a ses diagonales perpendiculaires alors c'est un losange.
•Si un parallélogramme a deux côtés consécutifs de même longueur alors c'est un
losange.
U
H
Y
T

5ème4 2009-2010
Exemple 1 (démonstration)
On considère un parallélogramme
UJHY
tel que
JH =HY
. Que remarques-tu ?
Démontre-le ?
•On remarque que
UJHY
est un losange.
•On sait que
UJHY
est un parallélogramme et que les côtés consécutifs
[JH ]
et
[HY ]
sont de la même longueur (
JH =HY
).
•Or, si un parallélogramme possède deux côtés consécutifs de même longueur alors
c'est un losange.
•D'où le résultat !
Exemple 2
On considère un parallélogramme
GHJK
de centre
O
. On suppose que
GOH =90°
. Fais
une figure à main levée. Que peux-tu dire ? Démontre-le.
GHJK
est un parallélogramme dont les diagonales sont perpendiculaires (
GOH =90°
).
Si un parallélogramme a ses diagonales qui sont perpendiculaires alors c'est un losange.
Donc
GHJK
est un losange.
Axes et centre de symétries
Si
ABCD
est un losange de centre
O
alors :
•
BD
et
AC 
sont des axes de symétrie ;
•
O
est un centre de symétrie.
U
J
H
Y
GH
J
K
O