TD Electrocinétique 2

PSI Brizeux
EXERCICES Électrocinétique 2
EXERCICES Électrocinétique 2
Filtrage
 El21 Diagrammes de Bode de systèmes fondamentaux du second ordre
Représenter les diagrammes de Bode en amplitude et en phase des fonctions de transfert suivantes (une
discussion en fonction du facteur d’amortissement sera à mener) :
1°) Passe-bas d’ordre 2 : H (jx) =
!
H0
1+2"(jx)+(jx)2
2°) Passe-haut d’ordre 2 : H (jx) =
!
H0(jx)2
1+2"(jx)+(jx)2
3°) Passe-bande d’ordre 2 : H (jx) =
!
H0
1+jQ(x "1
x)
4°) Coupe-bande d’ordre 2 : H(jx) =
!
H01+(jx)2
( )
1+2"(jx)+(jx)2
Classer les montages suivants (sortie ouverte) dans une des catégories précédentes, puis dans le cas du passe-
bas, déterminer le gain statique, la pulsation propre et le facteur de qualité.
ve(t)
L
C
vs(t)
R
A
ve(t)
L
C
vs(t)
R
B
ve(t)
L
C
vs(t)
R
C
ve(t)
L
C
vs(t)
R
D
Rép : A = passe-haut ; B = passe-bas ; C = passe-bande ; D = réjecteur ; cas du passe-bande : H0 = 1, ω0 = 1
LC , Q = Lω0
R
 El22 Réponse d’un système linéaire à une rampe de tension
Etant donné un système linéaire stationnaire initialement au repos et dont la réponse au signal échelon
u(t) est su(t), déterminer sa réponse, les conditions initiales étant les mêmes, à la rampe de position : e(t) =
atu(t) pour t > 0 et e(t) = 0 pour t ≤ 0.

PSI Brizeux
 El23 Identification d’un système linéaire.
L’essai à l’échelon unitaire de 2
systèmes linéaires (ordre 1 ou 2)
comprenant éventuellement un retard pur,
a donné les résultats représentés ci-
dessous. Identifier la nature et déterminer
graphiquement les paramètres
caractéristiques de ces systèmes.
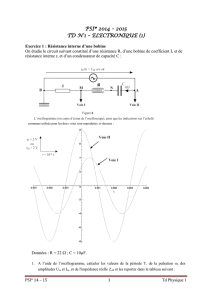
 El24 Identification d’un filtre.
Le relevé du diagramme de Bode en
amplitude et en phase d’un système
linéaire a donné les résultats
représentés ci-contre.
A quel type de filtre cela correspond-
il ? Evaluer alors approximativement
ses paramètres.
Rép : H0 = 10 ; ω0 = 10 rad.s-1 ; σ = 0,15

PSI Brizeux
 El25 Réponses indicielles de systèmes linéaires.
S1 et S2 sont deux systèmes linéaires et invariants dont les réponses à l’échelon unitaire sont données ci-
dessous :
1°) Proposer pour chacun de ces systèmes, une équation différentielle faisant intervenir les signaux d’entrée
et de sortie.
2°) En déduire la fonction de transfert et l’allure du diagramme de Bode de chaque système.
3°) Proposer une structure électronique simple pour chaque système (on pourra choisir A et B inférieures à 1
et n’utiliser que des composants résistifs et capacitifs purs.
 El26. Caractéristiques de filtres du premier ordre.
1°) Les graphes représentés ci-dessous donnent la réponse d’un filtre du premier ordre à un signal
triangulaire d’amplitude 1V, de fréquence 50 Hz et 10 kHz.
Déterminer le type du filtre et sa fréquence caractéristique.
2°) Les graphes représentés ci-dessous donnent la réponse d’un filtre du premier ordre à un signal créneau
d’amplitude 1V, de fréquence 100 Hz et 20 kHz.
Déterminer le type du filtre et sa fréquence caractéristique.
Rép : 1°) passe haut fc = 500 Hz. 2°) passe-bas fc = 1,5kHz

PSI Brizeux
 El27 Comportement fréquentiel d’un filtre. Réponse à un signal triangulaire
1°) Examiner rapidement le comportement basse fréquence et haute fréquence du système représenté ci-
dessous.
+
_
+
_
R
R
!R
R
C
C
e
s
A
A'
B
2°) Déterminer la fonction de transfert H= S
E . On la mettra sous la forme canonique généralement adoptée
pour un tel filtre : H = H0
1+jQ( ω
ω0 - ω0
ω ) . Quelles sont les expressions et les significations des termes H0, ω0 et Q ?
Donner l’équation différentielle reliant s(t) et e(t).
3°) Tracer le diagramme de Bode correspondant pour α=1 et α=10.
4°) e(t) est un signal triangulaire de valeur moyenne nulle, d’amplitude 2E0 et de période T.
On observe les réponses suivantes pour α = 10. Interpréter ces deux résultats (T0 = 2π/ω0)
en BF (T = 10 T0) en HF (T = 0,1 T0)
5°) a) On considère maintenant que la tension d’entrée ve est une tension en créneaux de période T, qui vaut
V0 pour 0 < t < T/2 et -V0 pour T/2 < t < T.
Donner le développement en série de Fourier de cette tension.
b) Que devient ce développement si ve=V0 pour -T/4 < t < T/4 et ve = -V0 pour T/4 < t < 3T/4 ?
c) Compte tenu des valeurs numériques précédentes, quelle doit être la valeur la fréquence de ve pour que
f0 = ω0/2π corresponde à la fréquence de l’harmonique 3 de la décomposition du 5°)a) ?
Quelles seront les amplitudes du fondamental et des harmoniques 2,3,4 et 5 à l’entrée et à la sortie du
montage ? On prendre V0 = 0,5V. Conclure.
Rép : : 1°) A H.F. et B.F. on a s = 0. 2°) H0 = -α/3, Q = 1
3 1+α , ω0 = 1 RC 1+α

PSI Brizeux
 El28. Filtre passe-haut du deuxième ordre à basse-fréquence
1°) Quelle est la fonction de transfert d’un filtre passe-haut du deuxième ordre ? Introduire le facteur de
qualité Q et x la fréquence réduite x = f/f0.
2°) Préciser les domaines dans lesquels un signal sinusoïdal de fréquence f peut être considéré comme
transmis sans atténuation, dérivé une fois, dérivé deux fois (il est nécessaire de discuter en fonction du facteur
de qualité).
3°) La fonction de transfert est HÏ(jx) = -x2
1+ 2jx - x2 (filtre de Butterworth) de fréquence caractéristique 10
kHz.
Le signal d’entrée est un triangle d’amplitude 1V et de fréquence 100 Hz. Quelle est qualitativement la
forme du signal de sortie ?
4°) Interpréter la forme du signal de sortie obtenu pour un signal créneau variant entre 0 et 1V et de
fréquence 100 Hz ?
Rép : : transmis sans atténuation pour ω
ω0 >> 1/Q pour Q < 1 ou ω ω0 >> 1 pour Q > 1 ; simple dérivation pour Q << 1 et 1/Q
>> ω
ω0 >> Q ; double dérivation pour ω ω0 << 1/Q pour Q > 1 ou ω ω0 << 1 pour Q < 1.
 El29 Filtre universel à fréquence de coupure commandée
On considère le dispositif de la figure 1 dans lequel les opérateurs « -int » sont ceux définis figure 2 et les
multiplieurs vérifient la loi p = k.u.v (k = 0,1 V-1) comme indiqué également figure 2. Tous les amplificateurs
opérationnels présents dans le dispositif sont idéaux et fonctionnent en régime linéaire.
Le signal d’entrée est noté e ; VC est un signal de commande continu qui permet de modifier certaines
caractéristiques des divers filtres obtenus (sorties s1, s2 et s2). VC peut varier de 0,1 à 10 V. On notera Hi la
fonction de transfert correspondant à la sortie si.
1°) Déterminer les fonctions de transfert Hi et donner l’allure de leur diagramme de Bode asymptotique.
Indiquer dans chaque cas de quel type de filtre il s’agit.
2°) On désire disposer, pour une valeur de VC, d’un filtre passe-bas dont le module de la fonction de transfert
varie le moins possible aux très faibles fréquences. Que peut-on proposer comme relation entre les divers
composants ? Ce choix est effectué par la suite.
3°) On souhaite obtenir une bande passante à –3 dB variant de 100 Hz à 10 kHz. Que proposez-vous ?
4°) Donner l’allure de la réponse indicielle (échelon de 1V) du filtre passe-bas obtenu pour VC = 10V puis
pour VC = 1V.