Géométrie synthétique - Gymnase Auguste Piccard

! ! Chloé!Romano!
! ! 3M4!
!!!
1!
T
T
Tr
r
ra
a
av
v
va
a
ai
i
il
l
l d
d
de
e
e M
M
Ma
a
at
t
tu
u
ur
r
ri
i
it
t
té
é
é
2
2
20
0
01
1
10
0
0
G
G
Gé
é
éo
o
om
m
mé
é
ét
t
tr
r
ri
i
ie
e
e s
s
sy
y
yn
n
nt
t
th
h
hé
é
ét
t
ti
i
iq
q
qu
u
ue
e
e
!
!
!
!
!
!
Q
Q
Qu
u
ue
e
el
l
lq
q
qu
u
ue
e
es
s
s
t
t
th
h
hé
é
éo
o
or
r
rè
è
èm
m
me
e
es
s
s
e
e
et
t
t
c
c
co
o
on
n
ns
s
st
t
tr
r
ru
u
uc
c
ct
t
ti
i
io
o
on
n
ns
s
s
c
c
cl
l
la
a
as
s
ss
s
si
i
iq
q
qu
u
ue
e
es
s
s
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!!
!
!!
!
!!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
C
C
Ch
h
hl
l
lo
o
oé
é
é R
R
Ro
o
om
m
ma
a
an
n
no
o
o 3
3
3m
m
m4
4
4
G
G
Gy
y
ym
m
mn
n
na
a
as
s
se
e
e
A
A
Au
u
ug
g
gu
u
us
s
st
t
te
e
e P
P
Pi
i
ic
c
cc
c
ca
a
ar
r
rd
d
d
8
8
8 n
n
no
o
ov
v
ve
e
em
m
mb
b
br
r
re
e
e 2
2
20
0
01
1
10
0
0
M
M
Ma
a
aî
î
ît
t
tr
r
re
e
e d
d
de
e
e T
T
TM
M
M :
:
: A
A
Al
l
le
e
ex
x
xa
a
an
n
nd
d
de
e
er
r
r M
M
Mü
ü
ül
l
ll
l
le
e
er
r
r

! ! Chloé!Romano!
! ! 3M4!
!!!
2!
!
!!
T
T
Ta
a
ab
b
bl
l
le
e
e!
!
!d
d
de
e
es
s
s!
!
!m
m
ma
a
at
t
ti
i
iè
è
èr
r
re
e
e!
!
!:
:
:!
!
!
!
!!
I
I
In
n
nt
t
tr
r
ro
o
od
d
du
u
uc
c
ct
t
ti
i
io
o
on
n
n*
*
*
*
*
*
*
*
*
P
P
Pa
a
ar
r
rt
t
ti
i
ie
e
e*
*
*s
s
sé
é
ém
m
mi
i
in
n
na
a
ai
i
ir
r
re
e
e*
*
*:
:
:*
*
*
*
*
*
LE RAPPORT DE SECTION :!...............................................................................................................................................!4!
•!Exemples :!...........................................................................................................................................................!4!
Remarques :!.................................................................................................................................................................!4!
Exemple de rapport de section :!............................................................................................................................!4!
•!Points conjugués harmoniques :!................................................................................................!5!
Exemple :!.......................................................................................................................................................................!5!
•!Complément :!.....................................................................................................................................................!6!
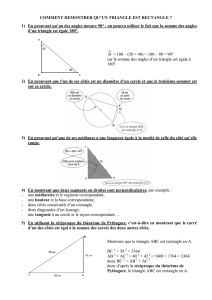
THEOREME DE PYTHAGORE :!...........................................................................................................................................!6!
•!Pythagore :!........................................................................................................................................................!6!
•!Première démonstration :!..................................................................................................................!7!
Théorème :!...................................................................................................................................................................!7!
•!Seconde démonstration :!.....................................................................................................................!8!
•!3ème démonstration :!..............................................................................................................................!10!
•!4ème démonstration :!..............................................................................................................................!11!
LE SEGMENT MOYEN D’UN TRIANGLE :!....................................................................................................................!12!
•!Démonstration du théorème :!......................................................................................................!13!
COROLLAIRE DU THEOREME PRECEDENT :!..............................................................................................................!13!
•!Preuve :!..............................................................................................................................................................!14!
QUELQUES LIGNES D’UN TRIANGLE :!......................................................................................................................!14!
THEOREME : (POUR LES MEDIANES)!........................................................................................................................!14!
UNE CONSTRUCTION :!...................................................................................................................................................!15!
•!Pour la réaliser :!................................................................................................................................!16!
THEOREME :!........................................................................................................................................................................!17!
THEOREME DE L’ANGLE INSCRIT :!.............................................................................................................................!17!
•!Démonstration :!.........................................................................................................................................!18!
•!Corollaire :!..................................................................................................................................................!18!
THEOREME DE PTOLEMEE :!...........................................................................................................................................!19!
•!Démonstration de l’implication directe :!................................................................!19!
THEOREME DES BISSECTRICES :!...............................................................................................................................!20!
•!Démonstration :!.........................................................................................................................................!20!
•!Réciproque :!..................................................................................................................................................!21!
LE CERCLE D’APOLLONIUS :!..........................................................................................................................................!22!
•!Marche à suivre :!...................................................................................................................................!22!
THEOREME DE CEVA :!.....................................................................................................................................................!22!
•!Propriété nécessaire :!.....................................................................................................................!23!
Preuve :!.......................................................................................................................................................................!23!
•!Démonstration du théorème de Céva :!...............................................................................!23!

! ! Chloé!Romano!
! ! 3M4!
!!!
3!
LA DROITE D’EULER :!......................................................................................................................................................!24!
•!Euler :!................................................................................................................................................................!25!
•!Théorème :!........................................................................................................................................................!25!
•!Démonstration :!.........................................................................................................................................!25!
THEOREME :!........................................................................................................................................................................!26!
•!Démonstration :!.........................................................................................................................................!26!
THEOREME DE NAPOLEON :!.........................................................................................................................................!27!
•!Énoncé :!..............................................................................................................................................................!27!
•!Preuve :!..............................................................................................................................................................!27!
1ère étape :!...................................................................................................................................................................!28!
2ème étape :!..................................................................................................................................................................!29!
•!Propriété nécessaire :!.....................................................................................................................!29!
•!Suite de la démonstration :!......................................................................................................!29!
LE PROBLEME DE FERMAT :!...........................................................................................................................................!30!
•!Propriété nécessaire :!.....................................................................................................................!30!
•!Suite démonstration :!.......................................................................................................................!31!
!
L
L
Le
e
es
s
s*
*
*p
p
pr
r
ro
o
ob
b
bl
l
lè
è
èm
m
me
e
es
s
s*
*
*d
d
d'
'
'A
A
Ap
p
po
o
ol
l
ll
l
lo
o
on
n
ni
i
iu
u
us
s
s:
:
:*
*
*
!
APOLLONIUS :!....................................................................................................................................................................!32!
LES PROBLEMES D’APOLLONIUS :!..............................................................................................................................!33!
DIX SITUATIONS :!..........................................................................................................................................................!33!
TROIS POINTS :!................................................................................................................................................................!35!
TROIS DROITES :!.............................................................................................................................................................!36!
•!Propriété nécessaire :!.....................................................................................................................!37!
Démonstration 1 :!....................................................................................................................................................!37!
Démonstration 2 :!....................................................................................................................................................!38!
DEUX POINTS ET UNE DROITE :!.................................................................................................................................!39!
UN POINT ET DEUX DROITES :!...................................................................................................................................!41!
•!Propriété nécessaire :!.....................................................................................................................!41!
Définition générale :!...............................................................................................................................................!41!
•!Résolution :!..................................................................................................................................................!41!
Justification :!..............................................................................................................................................................!43!
DEUX POINTS ET UN CERCLE :!.....................................................................................................................................!43!
•!Propriété nécessaire :!.....................................................................................................................!43!
•!Principe :!........................................................................................................................................................!44!
•!Construction :!............................................................................................................................................!45!
CONCLUSION :!...............................................................................................................!Erreur*!*Signet*non*défini.!
GLOSSAIRE :!.......................................................................................................................................................................!49!
‐!Un triangle est dit :!........................................................................................................................!49!
‐!Deux triangles sont dits :!..........................................................................................................!49!
REMERCIEMENTS :!...........................................................................................................................................................!50!
BIBLIOGRAPHIE :!..............................................................................................................................................................!50!
•!Livres utilisés :!...................................................................................................................................!50!
•!Sites internet consultés :!.........................................................................................................!50!
!
!!

! ! Chloé!Romano!
! ! 3M4!
!!!
4!
!
!
!
P
P
Pa
a
ar
r
rt
t
ti
i
ie
e
e!
!
!s
s
sé
é
ém
m
mi
i
in
n
na
a
ai
i
ir
r
re
e
e!
!
!:
:
:!
!
!
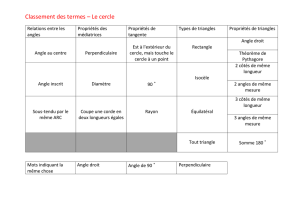
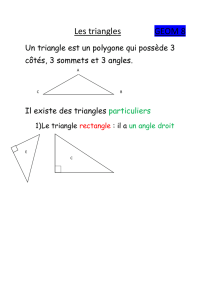
Quelques*définitions,*propriétés,*…*classiques*:*
!
!
LE RAPPORT DE SECTION :
!
Soit!A,!B!et!P!trois!points!alignés,!on!définit!le!rapport!de!section!(AB!;!P)!=!
!
"
!le!nombre!suivant!:!
!
AB
!=!
!
"
!
BP
!
Ce!nombre!
!
"
!définit!en!quelque!sorte!la!position!relative!de!ces!trois!points!alignés.!
!
• Exemples :
!
! (AB!;!P)!=!‐3!car!
!
AP
=!‐3
!
BP
!
!
! (AB!;!P)!=!‐1!car!
!
AP
=!‐1
!
BP
!
!
! (AB!;!P)!=!0!car!
!
AP
!=!0
!
BP
!
!
! (AB!;!P)!=!?!!car!
!
AP
!=!?!
!
BP
!
! (AB!;!P)!=!
!
"
!/!Impossible!
!
! (AB!;!P)!=!5!car!
!
AP
!=!5
!
BP
!
!
Remarques :
!
‐
!
"
!est!nul!si!P!se!trouve!en!A!
‐
!
"
!est!négatif!si!P!se!trouve!entre!A!et!B!
‐
!
"
!est!positif!si!P!se!trouve!à!l’extérieur!du!segment!AB!
!
Exemple de rapport de section :
!
A!et!B!sont!donnés,!voici!la!construction!du!point!P,!tel!que!(AB!;!P)=!
!
3
2
!
!
AP
=!
!
3
2
!
BP
!

! ! Chloé!Romano!
! ! 3M4!
!!!
5!
!
• Points conjugués harmoniques :
!
Soit!4!points!A,!B,!R!et!S,!alignés,!ces!4!points!sont!«!conjugués!harmoniques!»!si!:!
(AB!;!R)!=!‐(AB!;!S)!
!
Exemple :
!
(AB!;!R)!=!
!
2
3
!!
!
AR
!=!
!
2
3
!
BR
!
! Moyen!mnémotechnique!:!
(AB!;!S)!=!‐
!
2
3
!!
!
AS
!=!‐
!
2
3
!
BS
! Le!2!va!avec!le!A,!le!3!avec!le!B!
!
!
!
Par!Thalès!:!
!
AR
BR
!=!
!
2
3
!
!
AS!et!BS!sont!opposés!donc!nous!pouvons!déjà!être!sûr!que!le!coefficient!sera!négatif.!
!
!
AS
BS
!=!
!
2
3
!!AS!=!
!
2
3
!BS!!
!
AS
=‐
!
2
3
!
BS
!
!
!