Tronc commun

Page 1 sur 4
Correction bac blanc 2014 - Tronc commun
I- Le sonar des chauves-souris (8 pts)
1. Propriétés des signaux (2,75 pts)
1.1. (0,5 pt)
animal
durée
fréquence
Grand murin
< 1 ms
de 30 à 110 kHz
Grand rhinolophe
35ms
stable à 80 kHz puis décroit jusqu’à 65 kHz
1.2. (0,75 pt) son pur : vibration sinusoïdale dont le spectre sonore donne un seul pic
La fréquence fondamentale est la fréquence du son, associée au pic du premier harmonique sur le spectre sonore.
Les fréquences harmoniques correspondent à des fréquences multiples de la fréquence fondamentale : fn = n f1
1.3. (0,5 pt) Sur le graphique de la figure 2 on relève la fréquence fondamentale f1 30 kHz et les fréquences des
harmoniques
f2 60 kHz = 2
f3 90 kHz = 3
f4 120 kHz = 4 Donc la relation fn = n f1 est bien respectée
1.4. (0,25 pt) La composition en harmoniques d'un son est associée à son timbre.
1.5. (0,25 pt) Le phénomène qui peut perturber la détection d'un écho pour une cible de dimension inférieure à la
longueur d'onde du signal est la diffraction de l’onde par un obstacle.
1.6. (0,5 pt) La dimension minimale d’une proie est égale à la longueur d’onde =
=
= 4,3 10 3 m
2.Détection des distances (2 pts)
2.1. (0,25 pt) ∆t1 =
=
= 0,50 s
2.2. (0,75 pt) Les ultrasons parcourent la distance 2D ( aller-retour)
∆t2 =
donc ∆t2 =
=
= 0,018 s = 18 ms
2.3. (0,5 pt) Pendant cette durée ∆t2 , la chauve-souris s’est déplacée de : d = vcs ∆t2
d = 6,0 0,018 = 0,11 m
L’hypothèse formulée au 2.2. comme quoi on peut négliger le déplacement de la chauve-souris pendant la durée ∆t2 est
valable puisque 0,11 m est bien négligeable devant la distance D = 3,0 m.
2.4. (0,5 pt) Calcul de la distance parcourue par la chauve-souris en ∆t = 100 ms :
d’ = vcs ∆t = 6,0 0,100 = 0,60 m
La chauve-souris sera à une distance du mur égale à : D d’ = 3,0 – 0,60 = 2,4 m
Donc la chauve-souris pourra éviter le mur.
3. Détection d’une proie (1,25 pts)
3.1. (0,25 pt) En s'approchant d'une proie, les chauve-souris multiplient les émissions d'ultrasons pour affiner sa
localisation. Cette dernière étant très mobile, il faut de plus en plus de signaux au cours du temps pour conserver une
localisation précise.
3.2. (0,5 pt) La figure 2 montre que la chauve-souris s’approche de sa proie pendant la durée de l’enregistrement car on
observe que la durée entre l’émission et la réception de l’écho diminue. On observe aussi que la fréquence de l’écho
est supérieure à celle du signal émis. Ceci est dû à l’effet Doppler qui fait que la fréquence perçue est supérieure à la
fréquence émise.
3.3. (0,5 pt) Dans l’intervalle [40 ms – 100 ms] on observe 3 sons émis pour un intervalle de temps t = 100 – 40 = 60 ms
D’où le nombre de cris FC-FM par seconde : 3/0,060 = 50 cris par seconde.

Page 2 sur 4
4. Détection de la vitesse par effet Doppler (2 pts)
4.1. (0,75 pt) L’'effet Doppler se manifeste lorsqu’une source d’onde périodique est en déplacement relatif par rapport à
un récepteur. Il y a une modification de la fréquence du son perçu par rapport à celle du son émis.
Par exemple une voiture qui s’approche d’un observateur en klaxonnant de façon continue : l’observateur percevra un son
plus aigu quand la voiture s’approche et un son plus grave quand elle s’éloigne.
4.2. (0,25 pt) Lorsqu’une chauve-souris se dirige vers un mur, l’écho perçu a une fréquence fa plus grande que f émis.
4.3. (0,5 pt) Pour que fa > f , la relation correcte est la (2) fa =
CSson
CSson vv vv
f
En effet : vson+ vcs > vson –vcs et donc le rapport
CSson
CSson vv
vv
> 1 par conséquent fa > f
4.4. (0,5 pt) fa =
CSson
CSson vv
vv
f fa =
= 62 kHz
II- Physique et chimie dans le tennis (7 pts)
Partie A : Le service au tennis (3 pts)
Données : H =2,50 m v0 = 20,0 m·s-1
h = 90 cm D = 12 m
intensité de la pesanteur g = 9,8 m·s2.
1. Pour établir les équations horaires des
coordonnées du centre de la balle, il faut
d’abord déterminer son accélération.
(0,25 pt) Système étudié : la balle ; Référentiel : terrestre supposé galiléen ; Forces appliquées : le poids
= m.
(0,25 pt) Application de la 2ème loi de Newton : la masse étant constante :
=
= m.
Donc m.
= m.
On en déduit que l’accélération de la balle qui en chute libre est :
=
(0,25 pt) Coordonnées du vecteur accélération dans le repère (O,,
) :
ax = 0
az = g
(0,5 pt) Les coordonnées du vecteur vitesse sont les primitives des coordonnées du vecteur accélération car =
Les constantes d’intégration correspondent aux coordonnées de la vitesse initiale
: vox = v0 et voz = 0
vx = constante = v0
vz = g.t
(0,5 pt) Les coordonnées du vecteur position sont les primitives des coordonnées du vecteur vitesse car =
Les constantes d’intégration correspondent aux coordonnées du vecteur position initiale
: x0 = 0 et y0 = H
x = v0.t
z =
2. (0,5 pt) Pour établir l’équation de la trajectoire z = f(x) il faut éliminer le temps.
On a t =
que l’on reporte dans l’équation de z :
z =
=
On en déduit l’équation de la trajectoire du centre de la balle :

Page 3 sur 4
3. (0,75 pt) Pour savoir si la balle passera au-dessus du filet il faut calculer l’altitude z de la balle pour D = 12 m
Si z < h, la balle ne passe pas au-dessus du filet.
z =
=
= 0,74 m donc z < h = 0,90 m : la balle va dans le filet : service raté !
Partie B : La fatigue du joueur de tennis – (2 pt)
1. (0,5 pt)
CH3
CH COH
O
OH
2. (1,5 pt) Le spectre RMN présente 4 signaux : la molécule d’acide lactique présente 4 groupes de protons équivalents :
CH3
CH COH
O
OH
Les deux singulets et le quadruplet correspondent chacun à un proton et le doublet a un groupe de 3 protons équivalents
ce qui correspond aux dimensions des courbes d’intégration. Celle correspondant au doublet est 3 fois plus importante
que les 3 autres.
Détail : 0,5 pt pour le nbre de signaux + 0,5 pt pour la multiplicité + 0,5 pt pour l’exploitation de la courbe d’intégration
Partie C : Le cordage de la raquette de tennis – (2 pt)
1. (0,25 pt)
CO CH2COOH NH CH2NH H
n
45
2.1. (0,25 pt) H2N – CH2 CH2 CH2 CH2 CH2 NH2
2.2.1. (0,5 pt) pentan-2-one : (0,25 pt) groupe carbonyle (0,25 pt)
2.2.2. (1 pt)
(0,5 pt) spectre A : un grand pic à environ 1700 cm1 : caractéristique d’un groupe C=O
Il correspond donc à la pentan-2-one
(0,5 pt) spectre B : un large pic à environ 3300 cm1 : caractéristique d’un groupe NH
Il correspond donc à la pentane-1,5-diamine
groupe carboxyle
groupe hydroxyle
proton qui ne se couple pas :
singulet
proton qui ne se couple pas :
singulet
proton qui a 3 protons
équivalents voisins (CH3) :
quadruplet
3 protons équivalent qui ont 1
voisin : doublet

Page 4 sur 4
III Fatigue et acide lactique (5 pts)
1. L'acide lactique dans les muscles (1,5 pt)
1.1 (0,25 pt) ion lactate : C3H5O3
1.2 (0,5 pt) diagramme de prédominance :
C3H6O3 prédomine C3H5O3
prédomine
Dans le muscle pH = 6,6 > pKa = 3,9 donc C3H5O3 prédomine.
1.3 (0,25 pt)
eq363
eq
3eq353
a]OHC[
OH]OHC[
K
1.4 (0,5 pt)
6,6
4
eq363
eq353
pH
a
eq
3
a
eq363
eq353
10103,1
]OHC[
]OHC[
:.N.A
10
K
OH K
]OHC[
]OHC[
5,2 10 2
2. "Effets" de l'acide lactique (1 pt)
2.1. (0,5 pt) Une forte production d’acide lactique provoque une augmentation de la concentration des ions H+aq dans
l’organisme. Ces ions diminuent la production de l’ATP et viennent perturber le fonctionnement des muscles. Dans ce
cas, le sportif ne peut pas maintenir son effort physique.
2.2. (0,5 pt) Augmenter la capacité tampon d’un athlète permet de maintenir le pH à peu près constant et donc
d’empêcher le pH de diminuer pour éviter les conséquences citées dans la question 2.1. .
3. Titrage de l'acide lactique (document 4) : (2,5 pt)
3.1. (0,25 pt)
OHOHCHOOHC 2353363
3.2. (1 pt) A l’équivalence du titrage,
versé
ini363 HOn)OHC(n
et donc
E1ini363 V.C)OHC(n
(0,5 pt)
La quantité de matière d’acide lactique dosé dans la solution S est identique à la quantité de matière d’acide lactique
contenue dans l’échantillon de volume V = 2 ,0 mL (0,25 pt):
V.C)OHC(n aini363
donc
V
VC
CE.1
a
(0,25 pt)
3.3. (1 pt)
V)OHC(M.V.C
)OHC(M.CC 363E.1
363am
AN :
00,2 0,90.10.0,8.10.000,1
C33
m
0,36 g·L1 (0,5 pt)
%5
0,8 4,0
V
VU
E
E
%5,0
000,1 005,0
C
CU
1
1
%5,0
00,2 01,0
VVU
1
1
E
EC
CU
10
V
VU
et
V
VU
10
V
VU
E
E
donc
E
E
m
mV
VU
C
CU
(0,5 pt)
0,8 4,0
36,0CU:AN
V
VU
.CCU m
E
E
mm
0,02 g·L1
Cm = (0,36 ± 0,02) g·L1
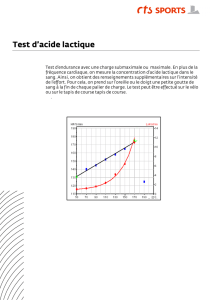
3.4. (0,25 pt) Pour une vitesse de 500 m/min, le cheval a une concentration en acide lactique très élevé (0,36 g·L1) par
rapport à celle (0,28g·L1) réalisée pendant le test d’effort trois semaines plus tôt. Le cheval n’est pas du tout en
meilleure forme, il a besoin de se reposer un peu…
3,9
pH
1
/
4
100%