Les filtres non récursifs

TP 4 . Filtres non récursifs
I. Le filtre moyenneur
!
Considérons!un!filtre!moyenneur!caractérisé!par!l’équation!de!récurrence!suivante!:!
!
𝑦!=
𝑥!+𝑥!!!
2!
!
1.!La!réponse!indicielle!est!donnée!par!les!valeurs!{yn}!quand!{xn}={1,1,1,1,1,...}!(la!
séquence!échelon!unité)!
A!l’aide!d’Excel!tracer!la!réponse!indicielle.!Compléter!le!tableau!:!
!
n!
F1!
0!
1!
2!
3!
4!
5!
xn!
0!
1!
1!
1!
1!
1!
1!
yn!
0!
!
!
!
!
!
!
!
Tracer!le!graphique!yn=f(xn)!
!
2.!Le!filtre!moyenneur!est!également!caractérisé!par!sa!transmittance!en!z,!notée!H(z).!!
Déterminer!la!transmittance!en!z,!notée!H(z)!du!filtre!moyenneur!en!faisant!les!
transpositions!suivantes!dans!l’équation!de!récurrence:!
!
!
3.!La!réponse!en!fréquence!d’un!filtre!numérique!se!détermine!dans!le!cas!où!le!filtre!
est!sollicité!en!entrée!par!un!signal!{xn}!correspondant!à!un!signal!sinusoïdal!de!
fréquence!f!échantillonné!à!la!fréquence!𝑓
!=!
!!
.!La!séquence!d’entrée!est!donc!
constituée!des!échantillons!xn!prélevés!à!la!fréquence!fE!=!2kHz!et!à!partir!de!la!date!
t=0!s,!sur!le!signal!x(t)=sin(2πf1t)!avec!f1=0,1fE.!
3.1.!Déterminer!l’expression!de!xn=x(nTE)!
3.2.!A!l’aide!d’un!tableur,!calculer!pour!0≤n≤19,!les!échantillons!yn!disponibles!en!
sortie!du!filtre.!
3.3.!Représenter,!pour!0≤n≤19,!les!échantillons!xn!et!yn.!
3.4.!En!déduire!l’amplification!H1=ymax/xmax!introduite!par!le!filtre!à!la!fréquence!f1!
lorsque!le!régime!permanent!est!établi.!!
3.5.!La!réponse!en!fréquence!d’un!filtre!numérique!est!donnée!par!sa!fonction!de!
transfert!complexe!𝑯(𝑗𝜔),!qui!se!déduit!de!la!transmittance!en!z,!H(z),!du!filtre!en!
effectuant!le!changement!de!variable!𝑧=𝑒!"!!!avec!𝜔=2𝜋𝑓!la!pulsation!du!signal!
d’entrée.!
4.!Donner!l’expression!de!𝑯(𝑗𝜔).!On!pourra!utiliser!la!relation!
𝑒!!!!!
!−𝑒!!!!! !=2𝑗𝑠𝑖𝑛(
𝜔𝑇
!
2)!
!
5.!Déterminer!le!module! 𝑯(𝑗𝜔)!et!l’argument!arg[𝑯(𝑗𝜔)].!
!
6.!On!note!𝑥=!
!!
!la!pulsation!réduite.!Quelles!sont!les!valeurs!de!x!qui!respectent!le!
critère!de!Shannon.!(Aide!:!donner!les!valeurs!de!f!pour!que!le!critère!de!Shannon!soit!
respecté,!calculer!ensuite!le!rapport! !
!!
!!ensuite! !
!!
!!pour!ces!valeurs).!
7.!Pour!0≤x≤0,5,!tracer!les!courbes!du!module!H(x)!et!de!la!phase!𝜑(𝑥)=arg 𝑯𝑗𝜔 !.!
!
8.!Selon!la!réponse!en!fréquence,!de!quel!type!de!filtre!s’agitFil!:!passeFbas,!passeF
bande!ou!passeFhaut!?!!
!
9.!Quelle!est!sa!bande!passante!?!
Rappel!:!La!bande!passante!est!donnée!par!l’intervalle!de!fréquences!pour!lequel!
𝐻(𝑥)≥!!"#
!!
!
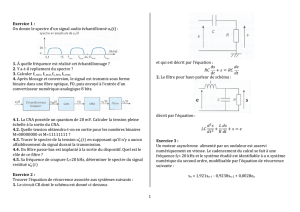
II. Un filtre non récursif
!
On!étudie!un!filtre!numérique!caractérisé!par!l’équation!de!récurrence!suivante!:!
yn!=!0,5(xn!F!xnF1)!
!
1.+Représenter!le!schéma!bloc!traduisant!l’algorithme!du!filtre.!
2.!Donner!l’expression!de!H(z),!sa!!fonction!de!transfert!en!z.!
3.!Déterminer!sa!fonction!de!transfert!complexe!𝑯(𝑗𝜔)!et!montrer!qu’elle!peut!
s’écrire!:!!
𝑯𝑗𝜔 =sin!(
𝜔𝑇
!
2)𝑒!(!
!!!!! !)!
!
On!pourra!utiliser!la!relation!
𝑒!!!!!
!−𝑒!!!!! !=2𝑗𝑠𝑖𝑛(
𝜔𝑇
!
2)!
!
4.!On!note!𝑥=!
!!
!la!pulsation!réduite.!Pour!0≤x≤0,5,!tracer!les!courbes!du!module!
H(x)!et!de!la!phase!𝜑(𝑥)=arg 𝑯𝑗𝜔 !.!
5.!Préciser!la!nature!du!filtre!(passeFbas,!passeFbande!ou!passeFhaut!)!et!sa!bande!
passante!sachant!que!la!fréquence!d’échantillonnage!adoptée!est!fE=10!kHz.!
!
!
!
!
Détermina'on!de!H(z)!à!par'r!de!
l’équa'on!de!récurrence!
!
"!
!
• La(transformée(en(z(
#$%!&'()*)+),*-!.$!+%$*/(,%0'1!1*!2-!*,+'1!3425-!&67*1!/'871*91!&1/!*,0:%1/!;<*=!
1/+!>!
3425?<@A<B2CBA!<"2C"!A<D2CDAEEEA!<*2C*AEEE!
<*!9,%%1/F,*&!G!.6'9H$*+)..,*!F%'.1I'!G!.6)*/+$*+!*JK!>!<*?<4*JK5!
Exemple':%La%transformée%en%z%de%{xn}={1,0,;1,2,0,0,000}%est%:%
X(z)=1;z;2+2z;3%
La%transformée%en%z%d’un%signal%échantillonné%est%le%polynôme%qui%a%comme%
coefficients%les%valeurs%du%signal.%
%
Exercice 2 :!L,**1%!.$!+%$*/(,%0'1!1*!2!&1/!/)M*$7<!&1!.61<1%9)91!B!>!;<*=!
4/'871*91!'9H1.,*!7*)+'51+!&1!;N*=!4.$!%'F,*/1!)*&)9)1..1!&7!().+%1!*70'%)871!OP5!
!
ii.1. Détermination de H(z) à partir de l’équation de
récurrence
!
P,**$)//$*+!.6'87$+),*!&1!%'97%%1*91!&67*!/N/+Q01-!,*!&'+1%0)*1!.$!
+%$*/0)++$*91!1*!2!1*!1((19+7$*+!.1/!+%$*/F,/)+),*/!/7)I$*+1/!>!
!
!!⟶!!!!!!!!!!⟶!!!!!!!!!!⟶!!!!!!!!!⟶!!!!!!!!!!
!
Exercice 3.!J%,7I1%!.$!+%$*/0)++$*91!1*!2!&7!().+%1!*70'%)871!F$//1C:$/!
41<1%9)91!B5E!
!
Exercice 4 :!L,**1%!.$!+%$*/(,%0'1!1*!2!&1/!/N/+Q01/!*70'%)871/!87)!/,*+!
&'9%)+/!F$%!.1/!'87$+),*/!&1!%'97%%1*91!/7)I$*+1/!>!
$5!N*?R<*C<*C"!
:5!N*?@-S4<*CN*CB5!
95!N*?@-S4<*AN*CB5AB-S<*CB!
!
iii.2. Détermination de l’équation de récurrence à partir de
H(z)
!
T)!.6,*!9,**$U+!V425!,*!F17+!&'+1%0)*1%!.6'87$+),*!&1!%'97%%1*91E!!
Exemple%:%Si,%pour%un%système%numérique%!!=!
!!!,%par%définition%!!=!(!) !(!).%On%
peut%donc%écrire%que%Y(z)(z+2)=X(z).%On%divise%l’égalité%par%z%et%on%obtient%:%
Y(z)(1+2z;1)%%=z;1X(z),%ou%Y(z)+%2z;1Y(z)=%z;1X(z).%On%utilise%ensuite%les%transpositions%
du%point%ii.1,%mais%en%sens%inverse%:%
!!!⟶!!!!!!!!!!⟶!!!!!!!!!⟶!!!!!!!!!!⟶!!!!%
%
On%obtient%:%yn+2yn;1=xn;1%ou%aussi%yn=%xn;1;2yn;1%
!
Exercice 5 :!L'+1%0)*1%!.6'87$+),*!&1!%'97%%1*91!&1/!/N/+Q01/!*70'%)871/!
87)!,*+!.1/!(,*9+),*/!&1!+%$*/(1%+/!'9H$*+)..,**'1/!/7)I$*+1/!>!
$5!!!=!
!!!!!"!
:5!!!=!!!
!!!,!!
95!!!=!!!!
!!!!
!
Annexe 1 : Réponses indicielles!
clear
//filtre analogique
//constante de temps tau=0,1 ms=1e-4 s
tau=1e-4;
//période échantillonnage
Te=5e-6;
Tmax=5*tau;
nb_points=Tmax/Te;
t=Te*(0:1:nb_points-1);
y=1-exp(-t/tau);
subplot(221)
plot2d2(t,y);
xtitle('réponse indicielle du filtre analogique','temps','y(t)');
//filtre numérique correspondant
alpha=tau/Te;
yn(1)=0;
x=ones(1,nb_points);
for i=2:nb_points do
yn(i)=(alpha/(1+alpha))*yn(i-1)+(1/(1+alpha))*x(i);
end
subplot(222)
plot2d3(t,yn);
xtitle('réponse indicielle du filtre numérique','temps','yn');
!