à la date t = 0 s.

Documents de Physique-Chimie – M. MORIN
1
Correction du devoir de Physique-Chimie DST2
TS
Durée : 3 h 30 min Date : vendredi 8 janvier 2016
M. MORIN
I. Aie ! J’ai une crampe. 7,5 points.
1. pH du sang et maintien de sa valeur
1.1.a) CO2 , H2O (aq) + H2O (l) = HCO3–(aq) + H3O+(aq) KA1 =
éq
éqéq aqOHCO aqOHaqHCO )](,[ )](.[)]([
22
33 
pH = pKa1 + log
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
1.1.b) log
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
= pH – pKa1
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
= 10pH–pKa1 = 107,4 – 6,1 = 101,3
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
= 20
1.1.c) Si [CO2 , H2O (aq) ] augmente alors le rapport
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
diminue.
On a établi que pH = pKa1 + log
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
Donc le pH doit diminuer, c'est d'ailleurs ce qu'indique le texte: "diminution locale du pH sanguin du fait
de la création en abondance de dioxyde de carbone dissous dans le sang".
1.2.a) Au voisinage du poumon, l'équilibre 2 est déplacé dans le sens de la consommation de O2.
La réaction 2 a lieu majoritairement en sens inverse. L'hémoglobine se charge de dioxygène.
1.2.b) Au voisinage du muscle, l'équilibre 2 est déplacé dans le sens de la consommation de CO2.
La réaction 2 a lieu majoritairement en sens direct.
1.2.c) Lors d'un effort l'hémoglobine réagit avec le dioxyde de carbone, il y a formation de HbCO2, ainsi
elle empêche une augmentation de [CO2 , H2O (aq) ] et empêche une baisse du pH.
La respiration, donc l'apport de O2, permet à l'hémoglobine de se "régénérer": elle libère du CO2 au niveau des
poumons et se recharge en O2. Ensuite HbO2 est acheminée par le flux de sang vers les muscles, où il y a libération
de O2 et capture de CO2.
2. L'acide lactique
2.1. Etude de l’acide lactique.
2.1.1. et 2.2.2.
Groupe carboxyle
Groupe hydroxyle
O
C
O
O
H
H
0,25
0,25
0,5
0,5
0,25
0,25
0,25
0,25
0,5

Documents de Physique-Chimie – M. MORIN
2
2.2. Analyse spectroscopique.
2.2.1. Analyse spectroscopique IR.
Le spectre n°1 correspond à l’acide lactique car la bande O – H n’est présente que dans le spectre n°1.
Bande fine vers 1750 cm-1 caractéristique de la liaison C = O
Bande large qui peut englober la liaison O – H (alcool) entre 3200 et 3700 cm-1 et la liaison O – H de l’acide
carboxylique (2500 – 3200 cm-1), non présente dans le deuxième spectre
2.2.2. Le nombre de signaux du spectre de RMN de l’acide lactique est égal au nombre de groupes de protons
équivalents dans la molécule. On observe 4 groupes de protons équivalents dans la molécule :
On obtient 4 signaux : 2 singulets, un doublet et un quadruplet.
2.3. Propriétés acido-basiques de l’acide lactique.
2.3.1. Un acide est une espèce chimique capable de céder un ou plusieurs protons H+.
2.3.2 CH3–CHOH–COOH (aq) + H2O (l) = CH3–CHOH–COO– (aq) + H3O+(aq).
L'acide lactique cède un proton à la molécule d'eau.
2.4. Couple Ox / Réd: acide pyruvique / acide lactique
CH3–CO–COOH / CH3–CHOH–COOH
soit en formules brutes: C3H4O3 / C3H6O3
demi-équation électronique: C3H4O3 + 2 e– + 2H+ = C3H6O3
L'acide pyruvique est le réactif et c'est l'oxydant; l'acide lactique est le produit et c'est le réducteur.
Il y a donc passage de l'oxydant au réducteur : c'est une réduction qui a lieu dans la cellule musculaire.
0,5
0,5
0,25
0,25
0,25
0,25

Documents de Physique-Chimie – M. MORIN
3
3. Variation locale du pH sanguin en l'absence des processus de maintien
3.1. réaction 3:
CH3–CHOH–COOH(aq) + HCO3–(aq) = CH3–CHOH–COO–(aq) + CO2,H2O(aq)
la constante d'équilibre de cette réaction a pour expression K =
22
3
[ ] .[ , ( )]
[ ] .[ ( )]
éq éq
éq éq
lactate CO H O aq
acide lactique HCO aq
On a la réaction de l'acide lactique avec l'eau:
CH3–CHOH–COOH (aq) + H2O (l) = CH3–CHOH–COO– (aq) + H3O+(aq).
avec Ka2 =
éq
éqéqlactiqueacide aqOHlactate ] [ )](.[][ 3
On a la réaction de l'acide carbonique avec l'eau:
CO2 , H2O (aq) + H2O (l) = HCO3–(aq) + H3O+(aq)
avec Ka1 =
éq
éqéq aqOHCO OHaqHCO )](,[ ].[)]([
22
33 
On remarque que K =
1
2
Ka
Ka
=
1
2
10
10 pKa
pKa
= 10(pKa1–pKa2) = 10(6,1–3,6) = 102,5
Soit K = 3,2 × 102
3.2. acide lactique ion lactate
Avancement
AH (aq) + HCO3– (aq) = A– (aq) + CO2,H2O (aq)
État initial
x= 0
n (mol)
n0 = 3.10–4
n1= [HCO3–]i  V
= 2,7.10–2  0,100
n1 = 2,7.10–3
n1 = 27.10–4
0
n3 =[CO2,H2O]i  V
n3 = 1,4.10–3  0,100
n3 = 1,4.10– 4
État intermédiaire
x
n0 – x
n1 – x
x
n3 + x
État final
x = xmax = 3.10– 4
0
24.10– 4
xmax = 3.10– 4
1,4.10– 4 + xmax = 4,4.10– 4
Si AH est réactif limitant alors n0 – xmax = 0 alors xmax = 3.10–4 mol
Si HCO3– est réactif limitant alors n1 – xmax = 0 alors xmax = 27.10–4 mol.
AH est donc réactif limitant car il conduit à l'avancement maximal le plus faible, xmax = 3.10–4 mol.
3.3. [HCO3–] f =
100,0 10.24 4
max1 
Vxn
= 2,4.10–2 mol.L–1
[CO2,H2O] f =
100,0 10.4,4 4
max3 
Vxn
= 4,4.10–3 mol.L–1 à cause de la réaction, il y a davantage de CO2 dissous.
3.4. D'après le 1.1.a) pH = pKa1 + log
éq
éq
aqOHCO aqHCO )](,[ )]([
22
3
pH = 6,1 + log
3
2
10.4,4 10.4,2
Après l’effort pH = 6,8
0,25
0,25
0,5
0,5
0,25
0,25
0,5

Documents de Physique-Chimie – M. MORIN
4
Exercice II. Les trois records de Felix Baumgartner. 7,5 points
Partie 1 : ascension en ballon sonde de Félix Baumgartner.
1.1. L’ascension du ballon a lieu sous l’effet de la poussée d’Archimède.
1.2. Système : {ballon ; équipage} Référentiel : le sol, référentiel terrestre supposé galiléen
Bilan des forces : Juste après le décollage
Le poids
P
(attention poids du ballon + de l’équipage)
La poussée d’Archimède
A
F
1.3. Le ballon peut décoller si les forces qu’il subit se compensent et qu’il possède une vitesse initiale non nulle
orientée vers le haut ; dans ce cas le mouvement est rectiligne uniforme.
Si la poussée d’Archimède prédomine sur la force poids alors le mouvement sera accéléré vers le haut.
Déterminons les valeurs des deux forces mises en jeu.
Le texte indique « c’est environ 3 tonnes qu’il a fallu soulever », donc msystème = 3×103 kg
Poids : P = msystème . g
P = 3×103 × 9,8 = 2,94×104 N = 3 × 104 N en ne conservant qu’un seul chiffre significatif.
Poussée d’Archimède : FA = ρair . V . g
Au niveau du sol (troposphère), on a ρair = 1,22 kg.m-3. Le volume initial du ballon est V = 5 100 m3
FA = 1,22 × 5100 × 9,8 = 60 975,6 N = 6,1×104 N
On constate que FA > P, ainsi le ballon peut décoller.
1.4. D’après le principe d’inertie (1ère loi de Newton), si le mouvement est rectiligne et uniforme, c’est que les forces
subies par le système se compensent.
0
A
P f F  
où
f
est la force de frottement de l’air.
Par projection suivant un axe vertical ascendant Oz :
Pz + fz + FAz = 0
– P – f + FA = 0
f = FA – P
f = ρair . V . g – m.systèmeg
f = 60 975,6 – 3×104 = 3×104 N
Partie 2 : saut de Félix Baumgartner
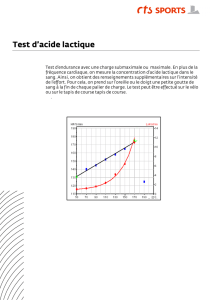
2.1. L’accélération est   
. On peut déterminer sa composante az suivant l’axe vertical ascendant en calculant le
coefficient directeur de la tangente à la courbe représentative de v = f(t) à la date t = 0 s.
Soient les points appartenant à la tangente O(0 ;0) et M(20 s ; 195 m.s-1).
az =
195 0
20 0
9,75 m.s-2 = 9,8 m.s-2 avec deux chiffres significatifs.
Comme
2
z
aa
, on constate que a g, ce qui est logique car le système subit essentiellement la force poids,
la force de frottement de l’air étant très faible à cette altitude.
2.2. D’après le texte introductif, Félix Baumgartner a atteint la vitesse de 1341,9 km.h-1
On divise par 3,6000 pour convertir cette vitesse en m.s-1.
v =
1341,9
3,6000
= 372,75 m.s-1
Cette vitesse est supérieure à la célérité du son quelle que soit la valeur de l’altitude fournie dans le tableau de données.
Félix Baumgartner a effectivement atteint une vitesse supersonique.
A
F
P
A
F
P
f
0,25
0,25
0,5
0,25
0,5
0,75
0,5
0,5

Documents de Physique-Chimie – M. MORIN
5
2.4. On regarde la courbe représentative de la vitesse en fonction du temps (courbe 1).
À la date t1 = 40 s, la vitesse augmente donc la force poids (orientée vers le bas) prédomine sur la force de
frottement de l’air (orientée vers le haut) : Schéma B.
À la date t2 = 50 s, la vitesse ne varie plus donc les forces se compensent : schéma C.
À la date t3 = 60 s, la vitesse diminue donc la force de frottement de l’air prédomine sur la force poids : Schéma A.
2.5. Le texte introductif indique que Félix ouvre son parachute au bout de 4 min et 20 s, soit au bout de 4×60 + 20 = 260 s.
À l’aide de la courbe 2, on lit z(t = 260 s) = 2,5 km.
Entre t = 260 s (ouverture du parachute) et t = 9 min 3 s = 543 s, Félix parcourt 2,5 km.
v =
dt
alors v =
3
2,5 10
543 260
soit = 8,8 m.s-1 = 9 m.s-1
On ne conserve qu’un seul chiffre significatif car la lecture graphique de l’altitude z(t = 260 s) est très approximative.
Partie 3 : Simulation du saut.
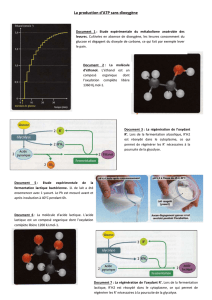
3.1. Description de l’évolution de la vitesse au cours du temps en distinguant les différentes phases.
On observe deux phases distinctes :
La première phase où les ballons subissent une accélération et leur vitesse augmente.
Une seconde phase où les ballons ne subissent plus d’accélération et où leur vitesse est constante.
3.2. Explication de la différence d’évolution de la vitesse dans cette simulation (graphique 1) et celle observée dans le saut
de Felix Baumgartner (courbe 1) ?
Félix n’évolue pas dans un milieu homogène. Lorsqu’il se rapproche du sol, l’atmosphère devient plus dense et même s’il
est moins rapide, il subit plus de frottements.
Les ballons par contre sont dans un milieu homogène car les variations de densité dans le local de l’expérience sont
négligeables.
Partie 4 : Modélisation mathématique de la chute des ballons.
4.1.
t (s)
vn+1 = vn + an. × t
an = 6,95 – 2,84 × vn+1
0
0
6,95
0,15
1,04
3,99
0,30
1,64
2,29
0,45
1,98
1,31
0,60
2,18
0,75
0,75
2,29
0,43
0,90
2,36
0,25
1,05
2,40
0,14
1,2
2,42
0,08
1,35
2,43
0,05
1,5
2,44
0,03
0,25
0,25
0,25
0,5
0,5
0,25
0,25
0,5