CH1-EC1 : Circuit Electrique en Régime Stationnaire : Circuit

I) Définitions Générales
I) Définitions GénéralesI) Définitions Générales
I) Définitions Générales
:
::
:
I.1) Définitions
I.1) DéfinitionsI.1) Définitions
I.1) Définitions
:
::
:
● Circuit électrique (ou réseau électrique)
Circuit électrique (ou réseau électrique)Circuit électrique (ou réseau électrique)
Circuit électrique (ou réseau électrique)
:
::
: Ensemble de composants reliés entre eux par des fils de jonction et
dans lequel circule un courant
● Dipôle
DipôleDipôle
Dipôle
:
::
: Composant à 2 bornes
● Nœud
NœudNœud
Nœud
:
::
: Point commun à au moins 3 composants
● Maille
MailleMaille
Maille
:
::
: Circuit électrique formant un contour fermé
● Branche
BrancheBranche
Branche
:
::
: Portion de circuit reliant 2 nœuds consécutifs
I.2) Illustrations
I.2) IllustrationsI.2) Illustrations
I.2) Illustrations
:
::
:
Illustrer sur les schémas suivants les définitions précédentes
Nombre de ?
Réseau(x) :
Dipôle(s) :
Nœud(s) :
Maille(s) :
Branche(s) :
I
II
II)
I) I)
I) Courant Electrique
Courant ElectriqueCourant Electrique
Courant Electrique
–
––
– Intensité
Intensité Intensité
Intensité
:
::
:
I
II
II.1) Définition
I.1) DéfinitionI.1) Définition
I.1) Définitions
ss
s
:
::
:
Un courant électrique
Un courant électriqueUn courant électrique
Un courant électrique est un
est un est un
est un DEPLACEMENT D
DEPLACEMENT DDEPLACEMENT D
DEPLACEMENT D’
’’
’ENSEMBLE
ENSEMBLEENSEMBLE
ENSEMBLE de porteurs
de porteurs de porteurs
de porteurs
de charges (électrons, ions, …) dans un conducteur (métal, l
de charges (électrons, ions, …) dans un conducteur (métal, lde charges (électrons, ions, …) dans un conducteur (métal, l
de charges (électrons, ions, …) dans un conducteur (métal, liquide, …)
iquide, …)iquide, …)
iquide, …)
Exemple d’un Métal
Exemple d’un MétalExemple d’un Métal
Exemple d’un Métal (solide)
(solide) (solide)
(solide)
:
::
: Exemple d’un liquide
Exemple d’un liquideExemple d’un liquide
Exemple d’un liquide
:
::
:
Particularité d’un matériau conducteur ? De quoi est constitué un liquide ?
Que se passe-t-il en l’absence de courant ? Que se passe-t-il en l’absence de courant ?
Que se passe-t-il en présence de courant ? Que se passe-t-il en présence de courant ?
Charge d’un électron ? Charge des porteurs de charges ?
D
1
D
2
D
4
D
3
D
6
D
5
Atomes fixes du matériau
Générateur
Générateur
CH1
CH1CH1
CH1
-
--
-
EC1
EC1EC1
EC1
: Circuit Electrique en Régime Stationnaire
: Circuit Electrique en Régime Stationnaire: Circuit Electrique en Régime Stationnaire
: Circuit Electrique en Régime Stationnaire
(
((
(
Part1
Part1Part1
Part1
)
))
)
–
––
– 1/
1/ 1/
1/3
33
3

Sens Conventionnel du Courant
Sens Conventionnel du CourantSens Conventionnel du Courant
Sens Conventionnel du Courant
:
::
: Sens de déplacement des charges positives
Sens de déplacement des charges positives Sens de déplacement des charges positives
Sens de déplacement des charges positives
Dans un circuit électr
Dans un circuit électrDans un circuit électr
Dans un circuit électrique
iqueique
ique
: Du + vers le
: Du + vers le : Du + vers le
: Du + vers le –
––
– EN DEHORS DU GENERATEUR
EN DEHORS DU GENERATEUR EN DEHORS DU GENERATEUR
EN DEHORS DU GENERATEUR
Attention : la charge d’un électron est négative Il se déplace du – vers le + en dehors du générateur
Intensité du Courant : Mesure la quantité de charge traversant le fil pendant un temps donné
Inten
IntenInten
Intensité = Débit de charges
sité = Débit de chargessité = Débit de charges
sité = Débit de charges
:
::
:
dq
i
dt
=
avec
I
II
II.2) Applications
I.2) ApplicationsI.2) Applications
I.2) Applications
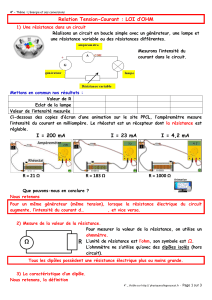
:
::
:
Valeur de l’intensité ?
Quel est le courant crée par un flux constant de 10
20
électrons de charge par secondes ?
Combien d’électrons traversent un fil dans le quel on mesure un courant continu de 1A ?
Signe de l’intensité ?
L’intensité peut-elle être négative ?
Qu’est-ce que cela signifie ?
Remarque : En général, on choisit arbitrairement le sens des flèches des courants, car on ne peut pas
toujours connaître initialement les sens réels de déplacement des courants dans les fils.
Si on obtient un signe positif, cela signifie que le sens choisit correspond bien au sens de
déplacement des porteurs de charge positives, sinon, il s’agit du sens opposé…
I
II
II
II
I.3) Loi des Noeuds
.3) Loi des Noeuds.3) Loi des Noeuds
.3) Loi des Noeuds
:
::
:
Loi des Noeuds
Loi des NoeudsLoi des Noeuds
Loi des Noeuds
:
::
: La somme des intensités des courants entrant dans un nœud
La somme des intensités des courants entrant dans un nœud La somme des intensités des courants entrant dans un nœud
La somme des intensités des courants entrant dans un nœud
est égale à
est égale àest égale à
est égale à la somme des intensités des courants qui en
la somme des intensités des courants qui en la somme des intensités des courants qui en
la somme des intensités des courants qui en sortent
sortentsortent
sortent
=
∑ ∑
j k
entran t so rtant
I I
Pourquoi ?
Application : Ecrire les lois des noeuds
Courants dans la même branche ?
i : l’intensité en Ampère (A)
q : la charge en Coulomb (C)
t : temps en secondes (s)
0 ?
I
<
I
4
I
1
I
3
I
2
B
I
3
I
1
I
2
A
I
4
I
1
I
3
I
2
C
D
1
D
2
D
6
D
5
I
1
I
5
I
6
D
4
I
4
I
2
D
3
I
3
I
7
I
8

I
II
II
II
II
II
I)
) )
) Potentiel
Potentiel Potentiel
Potentiel –
––
– Tension Electrique
Tension Electrique Tension Electrique
Tension Electrique
:
::
:
III.
III.III.
III.1
11
1)
) )
) Définitions
DéfinitionsDéfinitions
Définitions
:
::
:
Potentiel d’un point
Potentiel d’un pointPotentiel d’un point
Potentiel d’un point
:
::
: En tout point X d’un circuit électrique, on peut définir le potentiel V
X
, en Volts
Le potentiel qualifie l’état électrique de ce point
Masse M
Masse MMasse M
Masse M
:
::
: C’est la référence des potentiels – On fixe
0
M
V V
=
Symbole :
Tension
TensionTension
Tension entre 2 points
entre 2 points entre 2 points
entre 2 points AB
AB AB
AB
:
::
:
Additivité des
Additivité des Additivité des
Additivité des Tension
TensionTension
Tensions
ss
s
:
::
:
Démo :
III.2) Loi des mailles
III.2) Loi des maillesIII.2) Loi des mailles
III.2) Loi des mailles
:
::
:
Loi
Loi Loi
Loi des Mailles
des Mailles des Mailles
des Mailles :
::
: La somme algébrique des tensions le long d’une maille
La somme algébrique des tensions le long d’une maille La somme algébrique des tensions le long d’une maille
La somme algébrique des tensions le long d’une maille orientée
orientée orientée
orientée est toujours nulle
est toujours nulle est toujours nulle
est toujours nulle
0
ε
⋅ =
∑
i i
m aille
U
(Ne dépend pas de la nature des dipôles)
Exemple :
Méthode
MéthodeMéthode
Méthode Générale
Générale Générale
Générale
:
::
:
a) Identifier et ORIENTER la maille à étudier
b) Choisir un point de départ
c) Parcourir la maille en sommant les tensions
Avec un + si elles sont dans le sens de la maille
Avec un - si elles sont dans le sens opposé
d) La somme est égale à 0
CH1
CH1CH1
CH1
-
--
-
E
EE
E
C1
C1C1
C1
:
: :
:
Circuit Electrique en Régime Stationnaire
Circuit Electrique en Régime StationnaireCircuit Electrique en Régime Stationnaire
Circuit Electrique en Régime Stationnaire
(
((
(
Part1
Part1Part1
Part1
)
) )
)
–
––
– 2/
2/ 2/
2/3
33
3
M
A
AA
A
B
BB
B
AB A B
U V V
= −
BM B M B
U V V V
= − =
A
V
A B
U
AB
C
U
BC
U
AC
AC AB BC
U U U
= +
Avec
1 Si la tension est dans le sens de la ma
ille
1 Si la tension est dans le sens opposé
i
i
εε
=
= −
U
1
U
3
U
2
U
1
U
2
U
6
U
5
U
4
U
3
U
7

Exercice d’application
Exercice d’applicationExercice d’application
Exercice d’application 1
1 1
1
:
::
: Dans le circuit suivant, D
1
, D
2
, D
3
, D
4
et D
5
sont des dipôles quelconques.
Calculer les valeurs des intensités inconnues. Données : I
0
= 4A, I
1
= 1A, I
4
= 2A.
Physiquement, que signifie I
4
= 2A pour D
4
?
Combien d’électrons traversent le fil pendant
une seconde ?
Exercice d’application
Exercice d’application Exercice d’application
Exercice d’application 2
22
2
:
::
:
Dans le circuit suivant, D
1
, D
2
, D
3
, D
4
, D
5
et D
6
sont des
dipôles quelconques. Calculer les valeurs des tensions
inconnues. Données : U
2
= 4V, U
3
= 5V et U
6
= 10V.
IV
IVIV
IV)
) )
) Convention d’orientation et caracté
Convention d’orientation et caractéConvention d’orientation et caracté
Convention d’orientation et caractéristique d’un dipôle
ristique d’un dipôleristique d’un dipôle
ristique d’un dipôle
:
::
:
Deux
Deux Deux
Deux grandeurs sont nécessaires à caractériser l’état d’un dipôle
grandeurs sont nécessaires à caractériser l’état d’un dipôlegrandeurs sont nécessaires à caractériser l’état d’un dipôle
grandeurs sont nécessaires à caractériser l’état d’un dipôle
:
::
:
La TENSION
La TENSION La TENSION
La TENSION à ses bornes U
à ses bornes Uà ses bornes U
à ses bornes U
L’INTENSITE qui le traverse I
L’INTENSITE qui le traverse IL’INTENSITE qui le traverse I
L’INTENSITE qui le traverse I
I
II
IV
VV
V.1)
.1) .1)
.1) Convention d’orientation
Convention d’orientationConvention d’orientation
Convention d’orientation
:
::
:
De quoi s’agit
De quoi s’agitDe quoi s’agit
De quoi s’agit-
--
-t
tt
t-
--
-il
ilil
il
?
??
?
2
2 2
2 CONVENTIONS POSSIBLES
CONVENTIONS POSSIBLESCONVENTIONS POSSIBLES
CONVENTIONS POSSIBLES
La convention d’orientation dépend-elle du dipôle étudié ?
I
II
IV
VV
V.
..
.2
22
2)
) )
) Caractéristique d’un dipôle
Caractéristique d’un dipôleCaractéristique d’un dipôle
Caractéristique d’un dipôle
:
::
:
De quoi s’agit
De quoi s’agitDe quoi s’agit
De quoi s’agit-
--
-t
tt
t-
--
-il
ilil
il
?
??
?
Convention …………………
Convention …………………
D
1
D
3
D
2
I
1
D
5
I
5
I
0
I
3
I
7
N
I
2
I
6
I
4
D
4
P
Q
M
I
8
U
1
U
3
U
2
U
5
U
6
U
4
D
5
D
3
D
4
D
1
D
6
D
2

U : la tension en Volt (V)
R : la résistance du résistor en Ohm (Ω)
I : l’intensité du courant en Ampère (A)
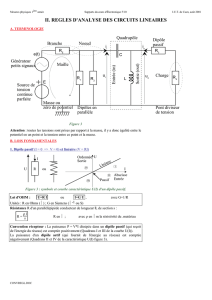
V) Conducteur Ohmique, ou Résistor
V) Conducteur Ohmique, ou RésistorV) Conducteur Ohmique, ou Résistor
V) Conducteur Ohmique, ou Résistor
V.1) Loi d’Ohm
V.1) Loi d’OhmV.1) Loi d’Ohm
V.1) Loi d’Ohm
:
::
:
Définition
DéfinitionDéfinition
Définition
:
::
: Un conducteur ohmique (ou résistor) est un dipôle qui limite le passage du courant, et
dans lequel la loi d’Ohm est vérifiée :
Loi d’Ohm
Loi d’OhmLoi d’Ohm
Loi d’Ohm
:
::
: En convention RECEPTEUR :
U R I
= ×
, avec
Cela provoque un effet thermique (échauffement), appelé effet Joule
Remarque : On utilise également la conductance
1
G
R
=
, exprimée en Siemens (S)
Caractéristique d’un Résistor
Caractéristique d’un RésistorCaractéristique d’un Résistor
Caractéristique d’un Résistor
:
::
:
Méthode
MéthodeMéthode
Méthode
: Retrouver la valeur de R à partir de la caractéristique
: Retrouver la valeur de R à partir de la caractéristique: Retrouver la valeur de R à partir de la caractéristique
: Retrouver la valeur de R à partir de la caractéristique
On mesure la caractéristique d’un résistor de résistance R inconnue :
Tension (en V) 0 5 10 15 20 25 30
Intensité (en mA) 0.0 2.2 4.5 7.0 9.0 11.4 13.7
Représenter la caractéristique U=f(I) de la résistance
Calculer la valeur de R à partir de la courbe tracée
V.2) Association en Série de Résistors
V.2) Association en Série de Résistors V.2) Association en Série de Résistors
V.2) Association en Série de Résistors –
––
– Pont diviseur de tension
Pont diviseur de tension Pont diviseur de tension
Pont diviseur de tension
:
::
:
Pont diviseur de Tension
Pont diviseur de TensionPont diviseur de Tension
Pont diviseur de Tension
:
::
: Lorsque 2 résistors sont en série, on peut exprimer directement la tension aux
bornes de chacun d’eux en fonction de la tension `totale` et des résistances.
R
RR
R
1
11
1
R
RR
R
2
22
2
R
RR
R
3
33
3
U
UU
U
I
II
I
I
U
1
U
2
U
R
1
R
2
CH1
CH1CH1
CH1
-
--
-
E
EE
E
C1
C1C1
C1
:
: :
:
Circuit Electrique en Régime Stationnaire
Circuit Electrique en Régime StationnaireCircuit Electrique en Régime Stationnaire
Circuit Electrique en Régime Stationnaire
(Part1)
(Part1) (Part1)
(Part1)
–
––
–
3
33
3/
//
/3
33
3
 6
6
1
/
6
100%