exercice-tuyere

Exercice :
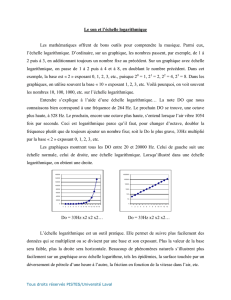
On étudie le fonctionnement de la portion de tuyère qui transforme une partie de
l’énergie thermique des gaz qui s’échappent de la turbine en énergie cinétique. Bien que très
rapide, l’évolution subie par les gaz est supposée quasistatique. On considère que les gaz sont
parfaits.
1) On étudie un profil de tuyère quelconque, c’est-à-dire dont la section S est une
fonction de x, l’axe des x étant l’axe de révolution de la tuyère. En appliquant le 1ier
principe des systèmes ouverts, et en considérant que le gaz ne reçoit pas de chaleur et
que la tuyère est horizontale, montrer que :
22
1
2
p a b b a
c T T v v  
. v étant la vitesse
des gaz.
2) En déduire une relation entre dT, R, M, et d(v2).
3) Donner la différentielle logarithmique de la loi de Laplace exprimée en variable (T, P).
4) Exprimer la masse volumique du gaz en fonction de la température et de la pression.
Donner la différentielle logarithmique de cette expression.
5) Donner la différentielle logarithmique de la conservation du débit massique.
6) On rappelle que la vitesse du son dans un gaz est donnée par
RT
cM
. Démontrer à
l’aide des questions précédentes que :
2
2
10
dS v dV
S c V
(théorème d’Hugoniot).
En déduire qu’il existe un domaine de vitesse où un élargissement de la tuyère
provoque une accélération du gaz. Quel profil doit-on donner à la tuyère pour générer
un écoulement supersonique ?