2-6

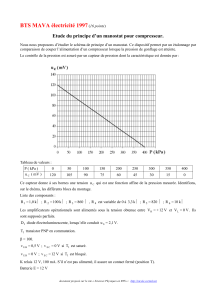
0- Condition amont
Le moteur étudié en conditions sol (0/0) avec Ps0et Ts0données :
Z = 0 m
Ps0= 101.3 kPa pour un débit d'air donnée de 100 kg/s
Ts0= 290 K
P0
101,3
kPa
T0
290
K
Da0
100,00
kg/s
D0
100,00
kg/s
α0
0,0000
-
M0
0,000
-
Cp0
1 004
J/(kg . K)
γ0
1,401
-
Hr0
1 014
-
H0
291 081
J/kg
Ps0
101,3
kPa
Ts0
290
K
V0
0,000
m/s
ρs0
1,217
kg/m3(calcul en GP)
0-2 Entrée d'air et manche avion
On considère les pertes de charge liées à l’entrée d’air et à la manche d’entrée d’air avion
sont négligeables : πMA = πEA = 1
P2
101,3
kPa Les autres paramètres tels que températures et pressions
statiques Ts2 et Ps2, vitesse V2 et nombre de Mach M2 ne
peuvent être calculés, les sections A2 étant inconnues.
T2
290
K
Da2
100,00
kg/s
D2
100,00
kg/s
α2
0,0000
-
M2-
Cp2
1 004
J/(kg . K)
γ2
1,401
-
Hr2
1 014
-
H2
291 081
J/kg
Ps2kPa
Ts2K
V2m/s
ρs2kg/m3
1

2-20 Manche d'entrée d'air moteur
La perte de charge liée à la manche d’entrée d’air moteur entre les plans 2 et 20 étant non
nulle : πMM = 0,992
P20
100,5
kPa
Les autres paramètres tels que température et pression
statiques Ts20 et Ps20, vitesse V20 et nombre de Mach
M20 ne peuvent être calculés, la section A20 étant
inconnue.
T20
290
K
Da20
100,00
kg/s
D20
100,00
kg/s
α20
0,0000
-
M20
-
Cp20
1 004
J/(kg . K)
γ20
1,401
-
Hr20
1 014
-
H20
291 081
J/kg
Ps20
kPa
Ts20
K
V20
m/s
ρs20
kg/m
3
20-3 Compresseur
Un considère un seul étage donnant un taux de compression de : πC= 8,5
et un rendement polytropique de : ηCpoly = 0,86
P3
854,2
kPa
Itération sur T
3:
Le calcul de T
3est issu de du calcul de Φ3, en tenant
compte du rendement polytropique.
Puissance nécessaire pour entraîner ce compresseur.
T3
582
K
Da3
100,00
kg/s
D3
100,00
kg/s
α3
0,0000
-
M3-
Cp3
1 043
J/(kg . K)
γ3
1,380
-
Φ3
9,692
USI
Hr3
2 049
-
H3
588 170
J/kg
Ps3kPa
Ts3K
V3m/s
ρs3kg/m3
WC
29 708 923
Watt
2

3-31 Prélèvement d'air
Les prélèvements d’air effectués en sortie du compresseur sont :
de ξ= 3 % pour le refroidissement de la turbine
et de β= 4 % pour le conditionnement d’air avion
P31
854,2
kPa
T31
582
K
Da31
93,00
kg/s
D31
93,00
kg/s
α31
0,0000
-
M31
-
Cp31
1 043
J/(kg . K)
γ31
1,380
-
Φ31
9,693
USI
Hr31
2 049
-
H31
588 170
J/kg
Ps31
kPa
Ts31
K
V31
m/s
ρs31
kg/m
3
31-4 Chambre de combustion
Le débit de carburant et la richesse afférente sont déterminés connaissant les
températures à l’entrée T31 et à la sortie T4de la chambre : T4= 1350 K
Le rendement de la chambre de combustion est de : ηcc = 0,992 et un PCI = 43 MJ/kg
La combustion engendre une perte de pression de 6%
P4
802,9
kPa
Débit carburant nécessaire.
T4
1 350
K
Da4
93,00
kg/s
D4
95,05
kg/s
α4
0,0220
-
M4-
Cp4
1 243
J/(kg . K)
γ4
1,300
-
Φ4
11,501
USI
Hr4
5 209
-
H4
1 495 309
JJ/kg
Ps4kPa
Ts4K
V4m/s
ρs4kg/m3
Dc4
2,05
kg/s
3

4-41 Sortie du redresseur (Turbine)
Le plan 40, là où la section de la veine A40 est minimale, le Mach M40 est sonique tant que le
distributeur de turbine est amorcé. Dans ce cas, les paramètres tels que température et
pression statiques Ts40 et Ps40, vitesse V40 et section A40 peuvent être calculés sachant que :
M40 = 1.
Le redresseur de turbine est refroidi par l’air prélevé en sortie du compresseur (ξ) qui est ré-
émis dans la veine en amont du plan 41.
P41
802,9
kPa
L’efficacité de mélange est égale à 1.
La température de mélange T41 est déterminée à partir du
principe de la conservation de l'enthalpie totale. Itérations
nécessaires sur Hr.
T41
1 329
K
Da41
96,00
kg/s
D41
98,05
kg/s
α41
0,0214
-
M41 -
Cp41
1 238
J/(kg . K)
γ41
1,302
-
Φ41
11,458
USI
Hr41
5 113
-
H41
1 467 554
J/kg
Ps41 kPa
Ts41 K
V41 m/s
ρs41 kg/m3
41-48 Sortie du rotor (Turbine)
La détente des gaz met en rotation la turbine et va entraîner le compresseur par l’intermédiaire
de l’arbre. Nous devons donc appliquer le principe de la conservation du travail entre la
turbine et le compresseur pour résoudre le système, en tenant compte des pertes éventuelles
(ηTP = 0,999).
Le prélèvement de puissance WPP étant quant à lui nul.
Un considère un rendement isentropique de ηTis = 0,85
P48
229,1
kPa
Calcul itératif sur T48 :
A partir de l'équilibre enthalpique ...
La pression P48 résulte de la détente réalisée dans la turbine
en intégrant le rendement de la turbine. Et donc passe par un
calcul itératif sur la température isentropique.
T48
1 074
K
Da48
96,00
kg/s
D48
98,05
kg/s
α48
0,0214
-
M48
-
Cp48
1 195
J/(kg . K)
γ48
1,316
-
Φ48
11,004
USI
Hr48
4 033
-
H48
1 157 776
J/kg
Ps48
kPa
Ts48
K
V48
m/s
ρs48
kg/m
3
T48is
1 028
K
Φ48is
10,914
USI
Hr48is
3 843
-
4

48-8 Tuyère
On considère le flux sortant de la tuyère en section 8, avec une perte de charge dans la tuyère
de :
(1 - πTU) = 1,2 %.
P8
226,4
kPa
P8 se calcule en intégrant la perte de charge dans la tuyère.
La température totale, les débits et la richesse se
conservent.
Déterminer si la tuyère a un fonctionnement critique (tuyère
sonique) ou adapté. Un premier niveau de vérification
s’opère en calculant le rapport P8 sur Ps0, et en le
comparant au rapport P8 sur Ps8 avec M8 = 1 calculé en
théorie des gaz parfaits.
A ce stade débute un calcul itératif basé sur une valeur a
priori de Ts8 qui permet de calculer Cp(Ts8 ,a8) et donc
γ
(Ts8
,
α8) puis V8 et H(Ts8 , α8) afin de vérifier l’équation
suivante dans laquelle H(Ts8 ,
α8) est connu :
Avant de déterminer les performances, il nous faut calculer
la section A8 à partir du débit réduit puis la pression
statiquePs8 en gaz réel.
T8
1 074
K
Da8
96,00
kg/s
D8
98,05
kg/s
α8
0,0214
-
M8
1,000
-
Cp8
1 195
J/(kg . K)
γ8
1,316
-
Φ8
11,004
USI
Hr8
4 032
-
H8
1 157 452
JJ/kg
Ps8
112,4
kPa
Ts8
925
K
V8
593,7
m/s
ρs8
0,423
kg/m
3
Cp8
1 163
J/(kg . K)
γ8
1,328
-
Hr8
3 420
-
Dr8
0,0397
USI
Φ8
10,700
USI
A8
0,3578
m²
Performances
Notons que Ps
8est supérieure à Ps0ce qui signifie que la tuyère est bien amorcée.
Calculer la poussée F, la consommation spécifique CS et les rendements.
F
62 185
NRappel :
Pour déterminer la vitesse V9’ qui correspond à la vitesse
des gaz en sortie tuyère pour laquelle on aurait Ps9’ = Ps0,
il faut tout d’abord calculer Ts9’ avec :
Pour atteindre la détente complète des gaz, i.e. Ps9’ = Ps0,
il faut bien que la vitesse des gaz en sortie tuyère
augmente, soit V9’ > V8.
FS
621,8
m/s
Dc4
7 379
kg/h
CS
1,187
kg/h/daN
ηp
0,000
-
ηthp
0,000
-
ηth
0,223
-
ηCarnot
0,785
-
Ps9'
101,3
kPa
Ts9'
904
K
V9'
632,7
m/s
Φ9'
10,655
USI
Hr9'
3 335
-
5