Comment repérer un point à la surface de la Terre ? Partie 1 : Quel

Comment repérer un point à la surface de la Terre ?
Partie 1 : Quel est le plus court chemin ?
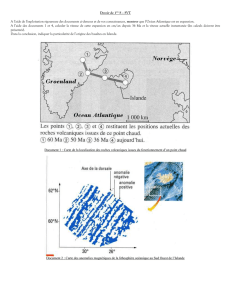
Quel le plus court chemin entre Miami et Gibraltar ? Celui de la trajectoire rouge
ou celui de la trajectoire orange ?
La trajectoire orange est-elle un segment de droite ?
Étude de la longueur de l'arc de cercle AB en fonction du rayon du cercle.
[AB] est un segment de longueur 10 cm.
P est un point mobile de la médiatrice de [AB].
Comment évolue la longueur de l'arc AB de centre P quand le rayon augmente ?
Quelques calculs
a est une mesure de l'angle APH.
Prouver que r = AB/(2 sin(a)).
Déterminer la longueur L de l'arc AB en fonction du rayon r et de l'angle a.
En déduire la longueur L en fonction de AB et de a.
Compléter le tableau :
Conclusion
Quel est le plus court chemin entre deux points A et B à la surface d'une sphère ?
Partie 2 : Une géométrie non euclidienne
1. Dans le plan
Rappeler la définition d’une droite du plan, d’un triangle, de deux droites parallèles.
2. Sur la sphère
On s'aidera de la sphère en polystyrène, des élastiques et des aiguilles pour marquer les points.
Sur la sphère de centre O, on donne deux points A et B.
Déterminer le plus court chemin de l’un à l’autre à la surface de la sphère.
Par deux points donnés A et B sur la sphère, combien passe(nt) de "droite(s)" ?
Combien de point(s) commun(s) peuvent avoir deux "droites" sur la sphère ?
3. Le triangle :
On donne trois points A, B et C sur la sphère.
Combien déterminent-ils de triangles sphériques ?
Quelle est la somme minimale des trois angles d’un
triangle sphérique ?
Peut-on construire un triangle rectangle, isocèle,
équilatéral ?
4. Les quadrilatères :
Les cercles, appelés parallèles en géographie, sont-ils des
"droites" parallèles ?
Peut-on déterminer deux "droites" parallèles à la surface
de la sphère ?
Comment définir un "parallélogramme" à la surface de la
sphère ? un carré ?
Partie 3 : Latitude et longitude
Le repérage d'un bateau en mer ne se fera pas à l'aide de trois coordonnées cartésiennes mais de trois
coordonnées sphériques : le rayon par
rapport au centre de la Terre (6400
km) et deux angles appelés latitude et
longitude :
45° est la latitude et 25° est la
longitude. La latitude de référence est
celle de l'équateur (0°) et la longitude
de référence est celle du méridien de
Greenwich.
Mais dire que le bateau est à 45° de
latitude et 25° de longitude ne suffit
pas à connaître sa position : il y a
quatre points possibles. On précisera
si la latitude est Nord ou Sud selon
que le bateau soit dans l'hémisphère
Nord ou Sud et si la longitude est Est
ou Ouest selon que le bateau soit à
l'Est ou à l'Ouest du méridien de
Greenwich.
1. Longueur d'un parallèle
On considère le paralléle de latitude q .
Déterminer, en fonction du rayon de la terre et de la latitude, la longueur de ce parallèle.
Quelle est la longueur des tropiques du Cancer et du Capricorne ?
Quel parallèle a pour longueur la moitié de l'Équateur ?
2. Expédition polaire.
En se déplaçant vers l'ouest sur le même parallèle sur 700 km, on se retrouve à son point de départ.
À quelle distance du pôle se trouve-t-on ?
3. En voyage !
On veut se rendre en avion de Bellin au Québec (70°W, 60°N) à Saint Pétersbourg (Russie 30°E, 60°N).
Vaut-il mieux suivre le parallèle 60°N ou passer par le Pôle Nord ?