SCHEMA 01 La « loi de l`utilité marginale décroissante » ou

SCHEMA 01
Initiation à la micro-économie - Fernando Martos - IAMM - 2011
Cette création est mise à disposition sous un contrat Creative Commons : utilisation non commerciale, sans modification.
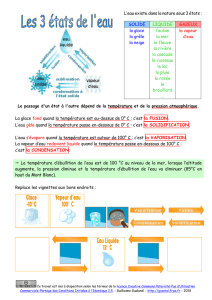
La « loi de l’utilité marginale décroissante »
ou « première loi de Gossen » (1811 - 1858)
Nombre de verres
0
1
2
3
4
5
6
7
8
9
10
Utilité totale
0
30
55
75
90
100
105
108
109
109
104
Utilité marginale
-
30 - 0 = 30
55 - 30 = 25
20
15
10
5
2
1
0
-5
L’Utilité Totale augmente à taux décroissant, passe par un
maximum avant de décroître.
L’Utilité Marginale (variation de l’Utilité Totale quand N varie) est
donc :
Positive décroissant puis
Nulle pour N = 9
Négative au-delà
Dans cette approche « Néo-Classique », l’Utilité Marginale est
supposée représenter la « Valeur d’Echange » que CET individu
reconnaît à telle unité de ce bien.
Supposons qu’il s’agisse ici de verres de « Coca-Cola ».
Il est clair que le fait même de considérer cet « objet » comme un
« Bien », c’est-à-dire comme quelque chose susceptible de
satisfaire un besoin (ici la Soif) dépend de l’individu considéré. Si
vous êtes allergique au « Coca-Cola » vous ne lui reconnaîtrait
aucune « Valeur d’Usage » dit autrement vous ne le
considérerait donc pas comme un « Bien ».
Tel n’est pas le cas de notre individu : il considère le « Coca-Cola »
comme un « Bien ». Reste qu’on suppose qu’au fur et à mesure
qu’il absorbe des verres… il a de moins en moins soif !
L’affirmation peut vous sembler triviale : elle est néanmoins
FONDAMENTALE puisque, comme nous le verrons par la suite
ce n’est que si nous acceptons ce postulat que nous serons en
mesure d’exprimer des fonctions de Demande « normales » (i.e :
décroissantes du prix) but ultime de ce début de cours !
L’Utilité Marginale (Valeur d’Echange) n’est au fond que le « prix
dans sa tête » que cet individu est disposé à payer. Dit autrement,
confronté à un prix P il ne consommera que les verres auxquels il reconnaît une
Um > P.
Il n’absorbera donc le verre n°9 (auquel il ne reconnaît aucune « valeur ») que si
untel accepte de lui offrir (P = 0 pour lui).
Il n’absorbera donc le verre n°10 (d’utilité négative pour lui) que si untel lui offre
ET l’indemnise de la désutilité qu’il éprouverait ! Ce dernier cas ouvrirait donc la
porte à la possibilité de prix négatifs !
On comprend donc que, pour la suite de nos propos, nous ne retiendrons que les
cas dans lesquels l’Utilité Marginale est ≥ 0.

SCHEMA 02
Initiation à la micro-économie - Fernando Martos - IAMM - 2011
Cette création est mise à disposition sous un contrat Creative Commons : utilisation non commerciale, sans modification.
0
UT
x
y
L’individu est confronté à deux biens. Sa « Fonction d’Utilité » (sur laquelle
nous reviendrons plus loin) indique l’évolution de l’Utilité Totale ressentie
par lui en fonctions des quantités de X et de Y.
Fixons la quantité de Y : nous examinons l’évolution de UT en fonction de la
seule variation de QX.
Nous retrouvons notre schéma 1 si X est du « Coca-Cola ».
L’Utilité Totale augmente à taux décroissant (pour Y donné lorsque QX
augmente). L’Utilité Marginale de X (dU / dx = tangente α) est donc positive
décroissante (tant que QX < Z).
UT
x
UMx
x
0
0
αα z
z
La « loi de l’utilité marginale décroissante »
En continu dérivable via la Fonction d’Utilité
Sens de vision

SCHEMA 03
Initiation à la micro-économie - Fernando Martos - IAMM - 2011
Cette création est mise à disposition sous un contrat Creative Commons : utilisation non commerciale, sans modification.
Dans un tel cas, l’Utilité Marginale serait croissante pour QX comprise entre O
et A « puis » décroissante (conforme à notre postulat) pour QX comprise entre
A et Z. Nous aurons à insister plus avant sur le fait que cette autre
présentation (donc ce type de fonction d’utilité) ne présente en fait que peu
d’intérêt (la Fonction de Demande serait croissante de son prix entre O et A !).
UT
x
UMx
x
0
0
Z
Z
A
A
La « loi de l’utilité marginale décroissante »
En continu dérivable via la Fonction d’Utilité non-homogène
0
UT
x
y
Sens de vision

SCHEMA 04
Initiation à la micro-économie - Fernando Martos - IAMM - 2011
Cette création est mise à disposition sous un contrat Creative Commons : utilisation non commerciale, sans modification.
UT
Q
UM
Q
EAU
DIAMANT
Interprétation « néo-classique » du paradoxe dit « de l’eau et du diamant »
Dans ses « Recherches sur la nature et les causes de la Richesse des
Nations » (1776), Adam SMITH (1723-1790) notait le paradoxe devenu
célèbre suivant :
La « Valeur d’Usage » de l’Eau est très importante (car il s’agit d’un bien
vital) alors que, hors conditions extraordinaires (désert…) sa « Valeur
d’Échange » est faible. À l’inverse,
La « Valeur d’Usage » du Diamant est faible (il n’est pas indispensable)
ce qui ne l’empêche pas d’avoir une forte « Valeur d’Échange » !
Rappel : Pour A. Smith, la « Valeur d’Échange » ou « Prix Réel » d’une
denrée quelconque pour celui qui désire l’échanger est « la quantité de
Travail que cette denrée le met en état d’acheter ou de commander ». Théorie
dite « objective de la Valeur.
En assimilant l’Utilité Totale à la « Valeur d’Usage » et l’Utilité Marginale à la
« Valeur d’Échange » certains auteurs néo-classiques prétendent (sur base
d’une théorie « subjective » de la Valeur) proposer une explication à ce
paradoxe.

SCHEMA 05
Initiation à la micro-économie - Fernando Martos - IAMM - 2011
Cette création est mise à disposition sous un contrat Creative Commons : utilisation non commerciale, sans modification.
La loi d’égalisation des Um pondérées par les prix
ou « seconde loi de Gossen » (1811 - 1858)
Qx
1
2
3
4
5
6
7
8
U totale X
80
150
210
260
300
330
350
360
UmX
80
70
60
50
40
30
20
10
Umx/Px
40
35
30
25
20
15
10
5
Umy/Py
100
70
60
40
30
20
10
10/3
U totale Y
300
510
690
810
900
960
990
1000
Qy
1
2
3
4
5
6
7
8
On suppose que le consommateur est « rationnel » et « preneur de prix ».
On suppose qu’il dispose d’un revenu R = 28
On se donne Px = 2 et Py = 3
L’individu « commence » par acheter une unité de Y (car 100 > 40). Dépense totale = 3.
Il achète « ensuite » une seconde unité de Y (car 70 > 40). Dépense totale = 6.
Il achète « ensuite » une troisième unité de Y (car 60 > 40). Dépense totale = 9.
Il achète « ensuite » une première unité de X & une 5° unité de Y (car 30 = 30). Dépense totale = 21.
Il achète « ensuite » une première unité de X (car 25 > 20). Dépense totale = 23.
Il achète « enfin » une 5° unité de X & une 6° unité de Y (20 = 20). Dépense totale = 28 = R.
C’est là son « panier optimal » (x* = 5 et y* = 6) : sous les contraintes qui sont les
siennes (R = 28) et des prix qui s’imposent à lui il ne peut mieux faire que UT = 300 + 960
= 1260.
Ce « panier optimal » est caractérisé par l’égalisation des utilités marginales pondérées
par les prix (20 = 20) ou « Seconde Loi de Gossen ». Dit encore autrement le rapport des
Um est égal au rapport des prix.
Il pourrait dépenser R = 28 autrement mais il
n’obtiendrait alors qu’un niveau U inférieur.
Exemple : pour x = 2 et y = 8 il dépense (4 + 24) = 28 mais
alors U = 150 + 100 = 1150 < 1260
Dans ce cas : UmX / UmY = 70/10 = 7 est > PX / PY = 2/3. Ne
pouvant « jouer » sur le rapport des prix il se doit de
diminuer le rapport des Um en substituant du X à du Y.
Il pourrait atteindre autrement ce niveau U = 1260
mais la chose supposerait alors que R > 28.
Exemple : pour x = 8 et y = 5 nous avons bien U = 360 + 900
= 1260 mais R = 16 + 15 = 31 > 28.
Dans ce cas : UmX / UmY = 10/90 = 0,111 est > PX / PY = 2/3.
Ne pouvant « jouer » sur le rapport des prix il se doit
d’augmenter le rapport des Um en substituant du Y à du X.