Découvrir la poussée d`Archimède

57
Découvrir la poussée d’Archimède
Objectifs
• Effectuer une recherche documentaire
• Formuler des hypothèses
• Proposer un montage expérimental répondant à un problème donné
Ressources
• feuille de papier, règle et crayons de couleur
• dynamomètre
• bécher de 150 mL
• éprouvette de 200 mL
• cristallisoir
• tubes en plastique avec bouchon de taille différente
• l
• boîte de masses marquées
• balance
• clous en fer
• eau
Déroulement
Avant de commencer
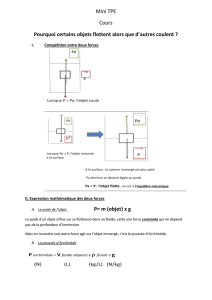
Archimède est un savant grec qui a le premier mis en évidence l’existence d’une force
exercée par l’eau sur tout corps immergé et qui s’oppose à la gravité : cette action
mécanique porte de nom de poussée d’Archimède. Elle est bien connue des adeptes
des sports nautiques. Le but de cette activité est de découvrir les travaux du célèbre
savant grec.
Mieux connaître les travaux d’Archimède
Effectuer une recherche documentaire sur Archimède en s’appuyant sur les pistes
suivantes :
• À quelle époque et dans quelle ville a-t-il vécu ?
• Quelles découvertes l’ont rendu célèbre ?
• Quelle expression lui attribue-t-on couramment ?
• Quelles sont les légendes qui entourent le personnage d’Archimède ?
Mise en évidence de la poussée d’Archimède
À l’aide d’un dynamomètre, peser successivement
une masse marquée suspendue dans l’air puis
totalement immergée dans l’eau. Relever dans
chaque cas la valeur de la force résultante
mesurée.
Représenter les forces qui s’exercent sur le solide
étudié dans les deux cas présentés. Identifier la
poussée d’Archimède et la calculer.
Physique-Chimie
4

58
De quoi dépend la poussée d’Archimède ?
En réfléchissant collectivement sur les facteurs susceptibles d’influencer la valeur de la
poussée d’Archimède, on peut penser qu’elle dépend de la masse immergée, du volume
de cette masse, de la masse volumique du liquide, de la profondeur d’immersion…
1. Pour vérifier l’influence de la masse, remplir un petit tube avec deux clous de fer et
refermer le soigneusement. Mesurer la force s’exerçant sur le tube dans l’air puis
dans l’eau. En déduire la valeur de la poussée d’Archimède. Reproduire la même
expérience avec quatre clous de fer. Conclure sur l’influence de la masse du solide
immergé.
2. Pour vérifier l’influence du volume, remplir un petit tube en plastique de clous et
refermer le soigneusement. Mesurer la force s’exerçant sur le tube dans l’air
puis dans l’eau. En déduire la valeur de la poussée d’Archimède. Placer le même
nombre de clous dans un tube plus gros. Et recommencer l’expérience. Conclure sur
l’influence du volume du solide immergé.
3. Pour vérifier l’influence de la profondeur d’immersion, remplir un petit tube en
plastique de clous et le refermer soigneusement. Mesurer la force s’exerçant sur
le tube dans l’air puis dans l’eau à deux profondeurs d’immersion différentes. On
pourra utiliser une éprouvette graduée. Conclure sur l’influence de la profondeur
d’immersion.
4. Pour vérifier l’influence de la masse volumique du liquide, remplir un petit tube en
plastique de clous et le refermer soigneusement. Mesurer la force s’exerçant sur le
tube dans l’air puis dans l’eau et enfin dans l’eau saturée en sel. Conclure.
5. Rassembler les résultats obtenus. En déduire l’expression de la poussée d’Archimède.
Formulation du théorème d’Archimède
Remplir un bécher d’eau à ras bord. Mesurer la force s’exerçant sur une masse
marquée dans l’air puis dans l’eau. Récupérer l’eau qui a débordé dans un cristallisoir.
Peser l’eau recueillie. Que remarque-t-on ? En déduire une formulation possible du
théorème d’Archimède.
Lien avec les autres disciplines
EPS : les sports nautiques.

59
Corrigé
• Mieux connaître les travaux d’Archimède
Archimède est un savant grec né en 287 avant JC et mort en 212 avant JC.
Il vécut à Syracuse, en Sicile, où il exerça ses talents de mathématicien, physicien et ingénieur.
On lui doit la poulie, le principe du levier, une méthode de calcul du nombre , le miroir parabolique...
Célèbre pour la formule « Eurêka » prononcée lors de la découverte de la poussée d’Archimède,
ce savant est aussi associé à de nombreuses légendes dont celle de la couronne du roi dont il a pu
démontrer qu’elle n’était pas en or.
• Mise en évidence de la poussée d’Archimède
On en déduit la valeur de la poussée d’Archimède :
 = 1,8 – 1,3 = 0,5 N.
• De quoi dépend la poussée d’Archimède ?
1. La masse du solide immergé n’a pas d’influence sur la
poussée d’Archimède.
2. La poussée d’Archimède augmente avec le volume du
solide immergé.
3. La poussée d’Archimède ne varie pas avec la profondeur d’immersion.
4. La poussée d’Archimède est plus importante dans l’eau salée qui est plus dense que l’eau douce.
5. D’après les résultats expérimentaux, la poussée d’Archimède est proportionnelle à la masse volu-
mique du liquide et au volume du solide immergé d’où  est proportionnelle à Úeau.Vsolide.
Le coefficient de proportionnalité est g.  = Úeau.Vsolide.g.
• Formulation du théorème d’Archimède
On remarque que la poussée d’Archimède est égale au poids du volume d’eau déplacé.
C’est le théorème d’Archimède.