Exercices d`électrocinétique

Exercices – ´
Electrocin´etique
■Calculs de tensions et de courants E2
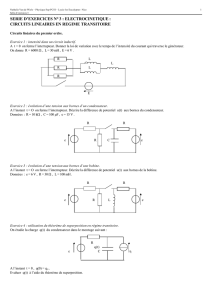
Ex-E2.1 R´eseau `a deux mailles
D´eterminer, pour le circuit ci-contre, l’intensit´e qui
traverse la r´esistance 2et la tension aux bornes de
la r´esistance 3:
1) en faisant des associations de r´esistances et en
appliquant le diviseur de tension.
R1
R3
R2
Eu
R4
i
2) en faisant une transformation Th´evenin →Norton et en appliquant le diviseur de courant.
3) Application num´erique pour = 6 ,1= 100 Ω, 2=3=4= 50 Ω
R´ep : 1/2) =3
13+ (1+3)(2+4);=3(2+4)
13+ (1+3)(2+4);
3) = 15 et = 15.
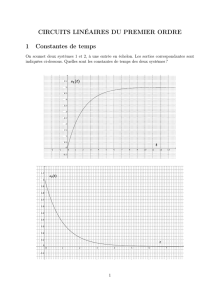
Ex-E2.2 Circuit lin´eaire
Dans le circuit ci-contre :
1) Calculer 𝐸𝐹 ,
2) Calculer l’intensit´e 0circulant dans
la branche principale ;
3) Calculer l’intensit´e ′circulant dans
la branche contenant le g´en´erateur ′
(pr´eciser son sens) ;
4) Calculer les intensit´es 1,2et 3.
Donn´ees :
= 1 Ω, = 5 et ′= 3 .
E2R
R
AB
E'
2R
R
R
R R
C
D
E
F
I0
i1
i2
i3
R´ep : 𝐸𝐹 ≃1;0≃083 ;′≃017 ;1=3≃033 ;2≃017 .
■Association de g´en´erateurs
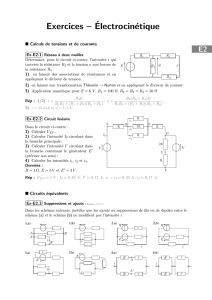
Ex-E2.3 Mod´elisation de Th´evenin (1)
Donner le g´en´erateur de Th´evenin ´equivalent au cir-
cuit ci-contre entre et .
R´ep : ´eq =
2et Th =+.
Ex-E2.4 Mod´elisation de Th´evenin (2)
D´eterminer le g´en´erateur de Th´evenin ´equivalent au
r´eseau dipolaire entre les bornes et ci-contre.
Donn´ees : = 1 ,= 6 Ω et = 24 .
R´ep : 𝑒𝑞 =
2= 3 Ω et 𝑇 ℎ = 2 +
4= 18
■Caract´eristique d’un dipˆole
Ex-E2.5 Groupement diode id´eale-r´esistances
Repr´esenter la caract´eristique Intensit´e-Tension () du
dipˆole ´equivalent au groupement entre les points A et B.
AB
U
R
R'
I

PTSI ∣Exercices – ´
Electrocin´etique 2009-2010
■Calculs de r´esistances ´equivalentes
Ex-E2.6 R´esistance ´equivalente d’un r´eseau dipolaire (1)
Calculer la r´esistance ´equivalente `a un r´eseau `a mailles carr´ees, chaque
cˆot´es ayant la r´esistance .
R´ep : ´eq =13
7
A
EG
D
C
M
N
F
B
I
I
Ex-E2.7 R´esistance ´equivalente d’un r´eseau dipolaire (2)
Chaque trait repr´esente un r´esistor de r´esistance .
D´eterminer la r´esistance ´equivalente de ce r´eseau vu des points :
1) A et C (54) 2) A et E (32) 3) A et F (78)
4) B et D (56) 5) H et D ()6) A et B (1724)
7) B et F (712)
ABC
HFD
GJE
Ex-E2.8 Th´eor`eme de Kennelly (`
A comprendre !)
On consid`ere les deux circuits ci-dessous : celui de
gauche est appel´e le circuit « étoile » et celui de droite
circuit « triangle ». Exprimer les résistances 1,2et 3
du circuit étoile en fonction des résistances 1,2et
3du circuit triangle pour que les deux circuits soient
équivalents. La relation obtenue constitue le théorème
de Kennelly.
R´ep : 1=23
1+2+3
,2et 3se d´eduisent par permutation circulaire des indices.
Ex-E2.9 R´esistance ´equivalente d’un r´eseau dipolaire (3)
1) Calculer la r´esistance ´equivalente du r´eseau suivant :
a. en utilisant les lois de Kirchoff.
b. en utilisant les regroupements de r´esistances (s´erie, pa-
rall`ele, triangle-´etoile).
2) On applique entre et une tension = 11 .
R
AB
C
D
R
R
RR
12
21
Calculer l’intensit´e du courant dans la branche CD avec : 1= 2,2= 4, et = 1 Ω.
R´ep : 1) ´eq =212+1+2
2+1+2
;2) =𝐶→𝐷=
11= 1 .
■Diviseur de tension
Ex-E2.10 ´
Equilibrage du pont de Weahtsone
Un pont de Weahtsone est un montage ´electrique
permettant de d´eterminer une r´esistance incon-
nue.
La r´esistance `a d´eterminer est 1.
Les r´esistances 3et 4sont fixes et connues.
2est une r´esistance variable dont on connaˆıt la
valeur.
Le pont est dit ´equilibr´e lorsque la tension
mesur´ee entre et est nulle.
1) D´eterminer la tension en fonction de et
des r´esistances 1,2,3et 4.
2) `
A quelle condition le pont est-il ´equilibr´e ? D´eterminer alors 1.
Donn´ees : 3= 100 Ω ; 4= 5 Ω ; 2= 1 827 Ω ; = 6 .
2http ://atelierprepa.over-blog.com/ jp[email protected]

2009-2010 Exercices – ´
Electrocin´etique ∣PTSI
3) Le voltm`etre indique la tension «= 0 » si, en réalité, on a : ∣∣1 .
→Dans le cadre de l’application numérique de la question 2), donner la précision sur la mesure
de 1.
Rép : 1) =3
3+4−1
1+2;2) 1= 365 Ω ;3) 1= 365±03 Ω
■LNTP / Th´eor`eme de Millman
Ex-E2.11 Th´eor`eme de Millman (1)
Déterminer la valeur de pour avoir = 2 :
1) après avoir simplifié le schéma (transformation(s)
Thévenin/Norton et association(s))
2) directement en utilisant le théorème de Millman.
Données :
= 10 ;= 1 ;1= 4 Ω ;2= 2 Ω.
R1
R2
R
EUη
Rép : = 1 Ω
Ex-E2.12 Th´eor`eme de Millman (2)
1) Énoncer la loi des nœuds en termes de potentiels pour
le nœud dans le montage ci-contre.
En déduire le courant dans la résistance .
2) Trouver cette même intensité en utilisant les trans-
formations Thévenin ↔Norton.
Rép : =123+231+312
123+(23+12+13)
E2
E3
E1
N
R1
R2
R3
R
i
Ex-E2.13 LNTP
Le nœud est connecté à la masse du circuit
de la figure ci-contre.
On donne : = 15 ;= 1 Ω et = 1 .
1) Déterminer les relations entre 𝐴,𝐶et
𝐷en appliquant la loi des nœuds en termes de
potentiels aux nœuds ,et .
2) Un voltmètre numérique, branché entre
et , mesure 𝐷𝐵 = 10 .
→En déduire les valeurs de 𝐴et 𝐶.
Rép : 𝐴= 24 et 𝐶= 18
2E
6E
3R
20R
4R
D
8E
20R
4R
AB
C
2R
η
Ex-E2.14 Th´eor`eme de superposition et
LNTP
Déterminer l’intensité du courant qui circule
dans la branche 2 2en considérant deux états
successifs du circuit et en appliquant le théorème
de Millman ou la LNTP.
Rép : =1
61
2+2
E1
2R
R
2R
E2
2R
2R
B1
A1A2
B2
M
i
jp[email protected] http ://atelierprepa.over-blog.com/ 3

PTSI ∣Exercices – ´
Electrocin´etique 2009-2010
Ex-E2.15 Exercice de rapidit´e [P5/41]
Dans les circuits ci-dessous, déterminer, par la méthode la plus rapide, la grandeur demandée.
Données : = 9 ;= 5 ;= 100 Ω
I ?
E2R 3R E
2R
R
U ?
η
2R
R
U ?
abc
I ?
E2R 3R
d
R
I ?
ER4R
e
RI ?
R4R
f
η
I ?
E2R 3R
g
R2R 3R
h
R
ηU ?
Rép : a) Loi de nœuds suivi de la loi d’Ohm :=1+2=
2+
3=5
6= 75 ;
b) Diviseur de tension : =2
2+=2
3= 6 ;c) Loi d’Ohm := 2 = 600 ;
d) Association « parallèle »puis loi de Pouillet :=
6𝑅
5+=5
11≃41 ;
e) Association « parallèle », loi de Pouillet puis diviseur de courant : 0=
4𝑅
5+=5
9et
=
4+0=
9= 10 ;f) Diviseur de courant : =
4+=
5= 1 ;
g) Loi d’Ohm :=éq=1
+1
2+1
3 =11
6= 165 ;
h) Loi d’Ohm :=
1
+1
2+1
3
=6
11 ≃273
Solution Ex-E2.1
1) Après avoir introduit et nommé les nœuds, on peut introduire la
résistance équivalente à 2et 4qui sont en série : 5=2+4
•Il apparaît que 3est en parallèle avec 5.
En simplifiant : 6=35=35
3+5
.
•On reconnaît un diviseur de tension, 1et 6étant en série,
soumises à la tension :
𝐴𝐵 =6
1+6
=35
3+5
1+𝑅3𝑅5
4𝑅3+𝑅5
Soit : =𝐴𝐵 =3(2+4)
13+ (1+3)(2+4)
•=𝐴𝐵
5
sur le premier schéma équivalent.
Soit : =3
13+ (1+3)(2+4).
Attention ! n’apparaît plus sur le second schéma équivalent. Il fallait revenir
au premier schéma équivalent pour l’exprimer.
4http ://atelierprepa.over-blog.com/ jp[email protected]

2009-2010 Exercices – ´
Electrocin´etique ∣PTSI
2) On introduit et on nomme les nœuds. On reconnaît un générateur
de Thévenin de f.é.m. et de résistance interne 1entre et .
On peut faire une transformation Thévenin →Norton.
Il apparaît le c.é.m. :=
1
.
•1et 3en paralèle, de résistance équivalente : 0=13
1+3
•0est en parallèle avec 5,mais on ne simplifie pas ! car :
- on cherche
- on reconnaît un diviseur de courant au nœud alimenté par :
=0
0+5
=13
1+3
1
𝑅1𝑅3
𝑅1+𝑅3+2+4
1
Soit : =3
13+ (1+3)(2+4)
•Puisque 𝐴𝐵 =5, on retrouve : =𝐴𝐵 =3(2+4)
13+ (1+3)(2+4)
3) = 15 et =𝐴𝐵 = 15
Solution Ex-E2.2
1) Montage « Diviseur de tension » entre et :𝐸𝐹 =
+ 2′= 1
2) •D’abord exprimer la résistance équivalente entre et :𝑒𝑞 = ()2=
22=2
5
•Du point de vue de la branche principale, la branche { 2 }est inutile puisqu’une force
éloctromotrice ′en parallèle impose la tension à ses bornes.
On peut donc l’enlever sur un schéma équivalent.
Il apparaît deux forces électromotrices en série qui s’oppose : on peut donc les remplacer par une
seule et unique f.é.m. de valeur 0=−′= 2 et de même sens que .
•Le circuit est maintenant équivalent à un circuit formé d’une seule maille
- parcourue par 0,
- constitué d’une f.é.m. 0de même sens que 0
- et d’une résistance équivalente 0=+𝑒𝑞 +=12
5.
→la loi des mailles donne 0=0
0
=5
12(−′) = 5
6≈083
3) •Pour connaître l’intensité ′circulant dans la branche contenant ′on calcule d’abord
l’intensité ′′ qui circule de vers dans la branche contenant les résistances 2+= 3
soumises à la tension ′.
La loi d’Ohm donne, en convention récepteur : ′′ =′
3= 1
•On en déduit donc, d’après la loi des nœuds et en définissant ′par rapport à ′en convention
générateur, que ′=′′ −0=1
6≈017 (′dirigée de vers ).
4) •Tout d’abord, les symétries imposent que 1=3.
On reconnaît ensuite entre et un diviseur de courant :
•On a donc : 1=1
𝑒𝑞
0=𝑒𝑞
0=⇒1=3=2
50=1
3≈033
•De même : 2=2
𝑒𝑞
0=𝑒𝑞
20=⇒2=1
50=1
6≈017
•On vérifie bien entendu la loi des nœuds en :0=1+2+3.
jp[email protected] http ://atelierprepa.over-blog.com/ 5
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
1
/
14
100%