Un algorithme de complexité O(|S|) pour

Un algorithme de complexité O(|S|) pour calculer la distance
de transfert entre deux partitions de S
Daniel Cosmin Porumbel1, Jin-Kao Hao2, Pascale Kuntz3
1Univ. Lille-Nord de France, UArtois, LGI2A
Technoparc Futura FSA, 62400 Béthune, France
[email protected]
2Université d’Angers, LERIA
2 Bd Lavoisier, 49045 Angers, France
[email protected]
3Laboratoire d’Informatique de Nantes Atlantique, Polytech’Nantes
BP 50609, 44306 Nantes cedex 3, France
[email protected]
Mots-clés :algorithme linéaire, distance de transfert, partitions proches
1 Introduction
En analyse de donneées et classification, il peut être utile de comparer des partitions entre elles
via une mesure de distance. Une des distances les plus utilisées est la distance de transfert étudiée
notamment par S. Régnier [5] dès les années 60 [5]. Plus formellement, soient kun entier positif
et Sun ensemble ; une partition est un ensemble de kclasses deux à deux disjointes, qui forment
un recouvrement de S. La distance de transfert entre deux partitions P1et P2est le nombre minimal
d’éléments qu’il faut transférer entre les classes du P1pour transformer P1en P2.
Des études précédentes [2, 3, 1] ont proposé une méthode de calcul fondée sur une réduction directe
au problème d’affectation et une résolution par la méthode hongroise (complexité entre O(|S|+k2)
et O(|S|+k3)). Dans cette communication, nous présentons un algorithme avec une complexité en
O(|S|)si certaines conditions de proximité entre partitions sont satisfaites. En pratique, si les parti-
tions sont de distance inférieure à |S|
5, le calcul peut être souvent effectué en O(|S|). De plus, nous
étendons l’algorithme à des partitions plus distantes mais qui partagent certaines classes en commun.
2 Distance de transfert et nouvel algorithme
Notons d(P1,P2)la distance de transfert entre P1et P2. D’une façon duale, la similarité s(P1,P2)
est définie par le nombre maximal d’éléments qui n’ont pas besoin d’être transférés entre des classes
de P1pour transformer P1en P2. Ainsi, la distance et la similarité satisfont l’équation s(P1,P2) +
d(P1,P2) = |S|. Pour calculer la similarité, il faut trouver une affectation σ:{1,2,...,k} → {1,2,...,k}
qui maximise la somme :
s(P1,P2) = max
σ ∑
1≤i≤k
Ti,σ(i)!,(1)
où Test une matrice k×kde similarité définie par Ti j =|Pi
1∩Pj
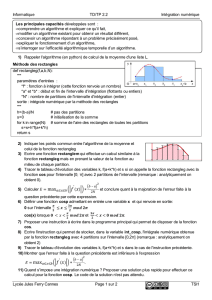
2|. La Figure 1 illustre le processus
de calcul de distance. La meilleure affectation sur cet exemple est : ¯ σ(1) = 1, ¯ σ(2) = 3 et ¯ σ(3) = 2.
Depuis les années 80, l’approche classique de calcul repose sur la transformation du problème en
un problème d’affectation linéaire qui se résout avec la méthode hongroise [3, 2, 1]. L’entrée de ce

P1: |1 2 3 4 | 5 6 7 | 8 9|
P2: |1 2 3 4 8 | 5 9 | 6 7|
=>
T(Mat. de Similarité)
4 0 0
0 1 2
1 1 0
=> Similarité = 7
Distance = |S| - 7 = 2
FIG. 1 – Un exemple de calcul de distance. Il suffit de transférer 2 éléments (8 et 5) pour transformer P2en P1.
Ainsi, la première classe de P1(i.e. {1,2,3,4}) devient égale à la première classe de P2; la deuxième classe de
P1(i.e. {5,6,7}) devient égale à la troisième de P2et la troisième classe de P1(i.e. {8,9}) devient égale à la
deuxième de P2.
problème est une matrice de coût k×k, et ainsi, l’algorithme de résolution doit inévitablement exécu-
ter au moins O(k2)pas pour lire toute l’entrée. Comme la méthode hongroise est dédiée uniquement
à des problèmes de minimisation, l’approche classique de calcul nécessite aussi une transformation
préalable de la matrice T.
Pour réduire la complexité à O(|S|), nous proposons de ne pas recourir au problème d’affectation et
d’exploiter le fait que l’entrée de notre problème contient juste O(|S|)éléments (les deux partitions).
De plus, la matrice Test une matrice creuse où seulement |S|éléments (au maximum) sont utilisés,
i.e. les éléments Ti j =|Pi
1∩Pj
2|avec i=P1(x)et j=P2(x), pour tous les x∈S. Pour les autres iet j
(s’il n’y a pas de x∈Stel que i=P1(x)et j=P2(x)), la valeur |Pi
1∩Pj
2|est forcement nulle.
À partir de ces observations, nous avons construit un algorithme [4] à deux étapes : (A) construire
la matrice de similarité T(P1,P2), et (B) déterminer l’affectation ¯ σmaximisant la somme (1). L’étape
(A) peut être toujours réalisée en O(|S|): (i) pour l’allocation de mémoire, il est possible d’utiliser un
allocateur au niveau de bloc de mémoire, (ii) pour l’initialisation, il suffit de parcourir les éléments
x∈S, et de modifier juste les valeurs TP1(x),P2(x). L’étape (B) peut être exécutée en O(|S|)uniquement
si certaines conditions sont satisfaites, e.g. si chaque classe de P1partage avec une classe de P2
au moins la moitié de leurs éléments. Dans ce cas, l’algorithme a besoin d’utiliser uniquement les
valeurs TP1(x),P2(x)(avec x∈S) pour trouver ¯ σet cela nécessite O(|S|)opérations.
Pour conclure, notons que cet algorithme peut être employé dans de nombreuses applications qui
calculent fréquemment des distances entre des partitions proches. Par exemple, en analyse des don-
nées, il faut souvent comparer une partition de référence (un étalon, le gold standard) avec une par-
tition déterminée par un algorithme. Des exemples similaires existent en analyse d’images, biologie,
partitionnement de données et clustering—voir des références en [4].
Références
[1] I. Charon, L. Denoeud, A. Guénoche, and O. Hudry. Maximum transfer distance between parti-
tions. Journal of Classification, 23(1) :103–121, 2006.
[2] W.H.E. Day. The complexity of computing metric distances between partitions. Mathematical
Social Sciences, 1 :269–287, 1981.
[3] D. Gusfield. Partition-distance : A problem and class of perfect graphs arising in clustering.
Information Processing Letters, 82(3) :159–164, 2002.
[4] C.D. Porumbel, J.K. Hao, and P. Kuntz. An efficient algorithm for computing the distance bet-
ween close partitions. Discrete Applied Mathematics, 159(1) :53–59, 2011.
[5] S. Régnier. Sur quelques aspects mathématiques des problèmes de classification automatique.
Mathématiques et Sciences Humaines, 82 :20, 1983 et 1965. (reprint of ICC Bulletin, 4, 175-
191, Rome, 1965).