1 S Activité documentaire L`analyse dimensionnelle : Bienvenue

1 S Activité documentaire
L’analyse dimensionnelle :
Bienvenue dans la 7ème dimension…
1. Présentation
D’après le physicien J.M. Lévy-Leblond, l’analyse dimensionnelle est “ une méthode générale à la fois
très simple, très profonde et très puissante, qui repose sur la compréhension de la nature des grandeurs
physiques en amont de leurs valeurs numériques. ”. Cette méthode est fondée sur l’étude de la forme
générale des équations physiques et permet d’obtenir des informations sur un phénomène physique en
tenant seulement compte du fait qu’il doit être décrit par une équation dimensionnellement correcte.
En effet, les équations utilisées en sciences physiques représentent des relations entre différentes
grandeurs physiques via un formalisme mathématique plus ou moins sophistiqué ; et, si le système
d’unités utilisé est cohérent, ces équations, pour posséder une certaine forme d’ « universalité »
doivent être indépendantes du système d’unités ; elles sont alors dites « homogènes ».
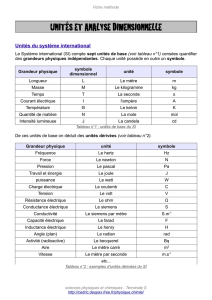
2. Dimension d’une grandeur physique
La dimension d’une grandeur physique représente sa nature physique.
Elle se note entre crochets et est symbolisée par une lettre majuscule (ex L pour une longueur)
Rem : la dimension est indépendante du système d’unités et de la valeur
numérique. Ainsi, une distance possède la dimension d’une longueur qu’elle soit
exprimée en nanomètre, en mètre, en pieds, en mile ou en année-lumière…
L’analyse dimensionnelle consiste alors à étudier les « dimensions » qui sont
attribuées aux grandeurs physiques courantes (surface, vitesse, accélération,
énergie...), compte-tenu des dimensions de 7 grandeurs prises comme
fondamentales
D'une manière générale il est possible d'exprimer la dimension de toutes les
grandeurs physiques en fonction de ces sept dimensions de base.
Grandeur
symbole
longueur
L
masse
M
durée
T
température
intensité électrique
I
intensité lumineuse
J
Quantité de matière
N
- par exemple une vitesse se définissant mathématiquement comme la dérivée d’une longueur par rapport au temps doit posséder
la dimension du rapport d’une longueur L sur une durée T soit [v] = L / T ou encore L*T-1 (ce que son unité doit révéler : m*s-1)
- de façon similaire, une accélération possède la dimension [a] = L*T-2, une force [F] = M*L*T-2 (facile à retrouver grâce à la
formule F = m*a)...
Rem : Il existe des grandeurs « purement numériques » qui ne possèdent pas de dimension.
Ex : rapport de 2 masses, de 2 forces et plus généralement de 2 grandeurs physiques de même dimension. Ainsi un angle plan,
qui est défini comme le rapport de 2 longueurs n’a pas de dimension. Il a cependant une unité : le degré ou le radian !
2.a. Travail : En vous aidant d’une équation (formule simple) bien choisie, déterminez les dimensions de la constante de
raideur d’un ressort k, d’une énergie, d’une puissance, d’une charge électrique, d’un champ électrique, d’une tension, d’une
résistance électrique, de la constante de gravitation universelle G.
3. Homogénéité d’une formule
L'analyse dimensionnelle repose sur le fait que ne peuvent être comparées que des grandeurs ayant la même dimension : il est
possible de comparer deux longueurs entre elles, mais pas une longueur et une masse entre elles par exemple. Ce postulat permet
donc de vérifier a priori la validité d’une équation.
En effet, une formule ne peut être valable que si les 2 membres de l’équation possèdent la même dimension.
Lorsque c’est le cas, on dit que la formule est « homogène ».
Ex : aN = v2 /  est une équation qui peut être valable car la formule est homogène. En effet, [aN] = L*T-2 et [v2 / [v]2 / []
= (L*T-1)2 / L = (L2*T-2) / L = L*T-2
Mais aN = v3 /  n’est pas une formule juste car elle n’est pas homogène : en effet, [aN] = L*T-2 et [v3 / [v]3 / []
= (L*T-1)3 / L = (L3*T-3) / L = L2*T-3 ≠ L*T-2

4. Applications de l’analyse dimensionnelle
L'analyse dimensionnelle permet de trouver intuitivement et rapidement la solution de
certains problèmes sans avoir à résoudre d'équations.
a. Chute libre verticale
Pour nous convaincre de la puissance de la méthode, revenons sur un exemple traité en
cours : la chute libre verticale dans le champ de pesanteur. On s’intéresse à la vitesse
atteinte par le corps.
Si on néglige les frottements, les seules grandeurs caractéristiques du problème sont la
masse m du corps, la hauteur de chute h, la durée t de la chute et la force responsable de
du mouvement c’est à dire le poids P.
Dans ces conditions, la vitesse v peut être exprimée sous la forme :
v = mx*hy*tz*Pk où x, y, z et k sont des exposants
La dimension d’une vitesse étant L*T-1 on peut écrire :
[v] = L*T-1 = [mx]*[hy]*[tz]*[Pk] = Mx*Ly*Tz*(M*L*T-2)k
en détaillant la dimension de la force que constitue le poids.
En regroupant les exposants par grandeurs dimensionnées, on obtient l’équation aux dimensions suivantes :
L*T-1 = M(x+k)*L(y+k)*T(z-2k) d’où on peut déduire les relations suivantes garantissant l’homogénéité de l’équation :
(x + k = 0), (y + k = 1) et (z - 2k = -1).
Puisque l’on a 3 équations et 4 inconnues, il faut fixer une inconnue. On peut le faire de plusieurs façons :
 Choisissons par exemple x = 0. On obtient alors : (0 + k = 0 soit k = 0), (y + 0 = 1 donc y = 1) et (z – 2*0 = -1 donc z = -1).
Finalement la vitesse s’exprime sous la forme v = m0*h1*t-1*P0 = h / t : cette formule est homogène donc a priori valable.
Nous savons cependant qu’elle n’est pas exacte dans notre cas précis car le mouvement n’est pas uniforme. C’est la limite
de la méthode qui ne peut pas nous affirmer que la formule trouvée sera la bonne !
Rem : une réflexion permet d’exclure cette formule qui ne prend pas en compte la « cause » de la chute à savoir le poids
 Choisissons alors y = 0. On obtient : (0 + k = 1 soit k = 1), (x + 1 = 0 donc x = -1) et (z – 2*1 = -1 donc z = 1).
Finalement la vitesse s’exprime sous la forme v = m-1*h0*t1*P1 = P*t / m = m*g*t / m = g*t : cette formule est homogène
donc a priori valable. Vous devez constater avec soulagement que la vitesse ne dépend pas de la masse comme ce que l’on
a vu en cours…
 Choisissons ensuite z = 0. On obtient : (0 - 2k = - 1 soit k = ½), (x + ½ = 0 donc x = - ½) et (y + ½ = 1 donc y = ½).
Finalement la vitesse s’exprime sous la forme v = m-1/2*h1/2*t0*P1/2 = √ (P*h / m) = √ (m*g*h / m) = √ (g*h) : cette
formule est homogène donc a priori valable. C’est la même que celle vue en cours à un facteur √2 près ! Ce coefficient sans
dimension n’a pas pu être trouvé par la méthode…
 Choisissons enfin k = 0. On obtient : (x + 0 = 0 soit x = 0), (y + 0 = 1 donc y = 1) et (z – 2*0 = -1 donc z = -1).
Finalement la vitesse s’exprime sous la forme v = m0*h1*t-1*P0 : On retrouve notre 1ère expression.
b. Pendule simple
Un pendule simple est constitué d’une bille considérée comme ponctuelle, de masse m,
attachée à un fil de longueur invariable l. Si on l’écarte de sa position d’équilibre vertical
d’un angle  et qu’on le lâche sans vitesse initiale, le pendule simple oscille dans le champ
de pesanteur.
On néglige les frottements, et on s’intéresse à la période d’oscillation du pendule que l’on
notera T0. Celle-ci correspond à la durée d’un aller-retour du pendule autour de sa position
d’équilibre.
b.1 Travail : En vous inspirant de la chute libre, trouver les grandeurs caractéristiques du
problème, la force responsable du mouvement et proposer une expression homogène pour
la période d’oscillation T0.
b.2 Travail : Proposer également une expression homogène pour la vitesse atteinte par la
bille lorsqu’elle passe à sa position d’équilibre vertical.
i
k
j
O
G
Position d’équilibre  = 0
l
m

c. Pendule élastique
Un pendule élastique est constitué d’un solide considéré comme
ponctuel de masse m attachée à un ressort de constante de raideur k.
Si on l’écarte de sa position d’équilibre horizontal (ressort au repos)
d’une distance x et qu’on le lâche sans vitesse initiale, le pendule
élastique oscille horizontalement autour de sa position d’équilibre
On néglige tous les frottements (support et air), et on s’intéresse à la
période d’oscillation du pendule que l’on notera T0. Celle-ci
correspond à la durée d’un aller-retour du pendule autour de sa
position d’équilibre.
c.1 Travail En vous inspirant de la chute libre, trouver les grandeurs caractéristiques du problème, la force responsable du
mouvement et proposer une expression homogène pour la période d’oscillation T0.
c.2 Travail : Proposer également une expression homogène pour la vitesse atteinte par le solide lorsqu’il passe à sa position
d’équilibre horizontal.
d. Mouvement des planètes
Considérons le mouvement de la Terre autour du Soleil. Nous considérerons que sa trajectoire est circulaire de rayon r =
150*106 km. On s’intéresse à la période du mouvement que l’on notera T0. Celle-ci correspond à la durée mise par la Terre pour
faire un tour autour du Soleil. Si on néglige la masse de la Terre par rapport à celle du Soleil, les grandeurs caractéristiques du
problème sont : le champ gravitationnel solaire responsable du mouvement GS = GMS / r2, la masse MS du Soleil et le rayon r de
l’orbite de la Terre.
d.1 Travail proposer une expression homogène pour la période T0. Pour vérifier votre proposition, calculer sa valeur en jours
sachant que r = 150*106 km, MS = 1,99*1030 kg et G = 6,67*10-11 SI. Si le résultat ne vous satisfait pas, multipliez-le par le
coefficient numérique sans dimension 2π, qui intervient fréquemment dans les mouvements circulaires…
d.2 Travail : Proposer également une expression homogène pour la vitesse de la Terre sur son orbite et calculer sa valeur.
e. Bombe nucléaire
Voici un autre exemple particulièrement intéressant dans la mesure où il viole un secret
militaire bien gardé : l'énergie dégagée par l'explosion des premières bombes nucléaires
était en effet secrète, jusqu'à ce qu'un spécialiste de la physique des fluides fasse le simple
raisonnement suivant. La brutalité même d'une explosion nucléaire a pour effet que les
détails fins du processus initial comptent très peu dans le développement du chapeau du
« champignon », qui est sphère de gaz en expansion dont la frontière est donnée par l'onde
de choc et qui se propage à partir du point de l'explosion.
Le rayon r de cette sphère à un instant t ne dépend donc, en première approximation, que
de l'énergie E dégagée par l'explosion, et de la masse volumique de l'air, dont la
résistance à la compression est a l'origine de l'onde de choc.
L'analyse dimensionnelle fixe sans ambiguïté la cinématique de l'explosion et conduit à la relation fonctionnelle suivante qui n'a
rien d'évident à priori : r = k*E1/5*
-1/5*t2/5 (1)
où k est une constante sans dimension qui doit normalement être de l'ordre de l'unité (voir activité « la physique qualitative »).
Le film d'une explosion nucléaire, rendu public, un peu inconsidérément sans doute par un état-major qui ne soupçonnait pas la
puissance de l'analyse dimensionnelle pour évaluer celle, alors secrète, de ses bombes, fut examiné par G. 1. Taylor en 1950. Il
constata que la sphère se dilatait bien suivant la curieuse loi en puissance deux cinquièmes du temps (d'où une vitesse
d'expansion décroissante et cette étrange impression de ralentissement que donnent tous les films, nombreux aujourd'hui, de ce
terrible spectacle). Ce n'était plus alors qu'un jeu d'enfant d'inverser la relation (1) et, à partir d'une évaluation de et de t, d'en
déduire E, 1'énergie dégagée par la bombe. C’est ce que nous allons faire.
Position d’équilibre : x = 0
x
k
m
Soleil
Terre
Ecliptique
MS
r

e.1 Travail
 Trouver les dimensions de [r] = ………….., [t] = ………….., [E] = ………………... et [ ] = …………………
 Trouver les dimensions de [E] / [ ] et de [r]5 /[t]2 et en déduire l’expression E = k’* *r5 / t2 (2) où k’ est une
constante sans dimension (voisine de l’unité). Cette expression n’est qu’une reformulation de l’expression (1)
 En déduire un ordre de grandeur de l’énergie dégagée dans une bombe nucléaire sachant que
air = 1,3 kg/m3
t = 4 s
t = 8 s
t = 16 s
t = 28 s
t = 46 s
Explosion d’une bombe nucléaire américaine en 1953. Le temps indiqué correspond à l’intervalle écoulé depuis l’explosion.
L’échelle spatiale est la même pour toutes les photographies (4 km 2,5 km).
f. Pythagore et la chute des chats…
 L’analyse dimensionnelle a également permis de comprendre
les résultats d’une enquête très sérieuse aux USA sur les « chances
de survie des chats qui tombent des balcons d’un immeuble en
fonction du nombre d’étages ». Les résultats statistiques
présentent globalement l’allure suivante (figure à droite : en
ordonnée figure le pourcentage de décès).
L’énigme consiste à interpréter la « redescente » de la courbe au
delà de 7 étages car le bon sens nous dit que « plus c’est haut, plus
c’est dangereux ! ».
En fait, un chat tombant d’un immeuble n’est pas un bon sujet d’étude de la véritable chute libre à
cause de la force de frottement exercée par l’air lors de la chute et qui s’opposent au poids (le chat
n’est donc pas soumis qu’à son poids comme l'exige la véritable chute libre).
Les vitesses de chute pouvant être importantes, une loi phénoménologique montre que la force de
frottement (F) est proportionnelle au carré de la vitesse (soit v2) ainsi qu’à la surface S de « prise
au vent » que le corps « offre » au cours de sa chute. Dès que la hauteur de chute dépasse une
vingtaine de mètres (pour un chat), cette force de frottement peut compenser exactement le poids
du chat si bien que celui-ci se retrouve pseudo-isolé (somme des forces vectorielles nulle) et sa
vitesse reste constante (d’après le principe d’inertie) ; on parle de vitesse limite atteinte vlim.
- La première partie (a) de la courbe s’interprète assez bien en assimilant la chute des chats, en dessous de 6 étages à une chute
libre (faible vitesse de chute donc faible force de frottement). Les lois de la chute libre nous apprennent que v2 = 2g*h, c’est-à-
dire que la vitesse d’arrivée au sol (en grande partie responsable des dégâts occasionnés chez nos matous) est proportionnelle à
la racine carrée de la hauteur de chute. Ainsi le pourcentage de décès augmente logiquement avec le nombre d’étages.
- Le palier (b) s’interprète en mettant le problème en équation : la compensation du poids P par la force de frottement F s’écrit
dimensionnellement: P = F soit m*g = k*S*v2 (avec k une constante dépendant des propriétés de l’air et de la « géométrie » du
chat). De cette expression on peut tirer v = ( m*g / k*S ) = constante = vlim pour une masse donnée et pour une position du chat
donnée (c’est-à-dire une surface de prise au vent S fixée). Ainsi, à partir d’une certaine hauteur correspondant à 7 étages environ,
la vitesse d’arrivée au sol (donc indirectement le pourcentage de décès) est constante et ne dépend plus de la hauteur de chute, ce
qui explique le palier.
- Que se passe-t-il au delà de 9 étages ? De fait, la formule précédente est toujours valable mais, par rapport au cas précédent,
c’est l’attitude du chat qui change. Pour des hauteurs inférieures à huit étages, la durée de la chute n’excède pas 4 secondes et le
chat, pendant qu’il tombe et par réflexe (il se sent en danger), se met « en boule » en se hérissant (comme lorsqu’il est attaqué).
Cette attitude de défense minimise la valeur de S et maximise alors la valeur de vlim (voir formule). Au bout de 8 étages de chute,
le chat commence à réaliser que son seul agresseur est la force de pesanteur; en clair qu’il tombe. Il adopte alors une attitude
instinctive tout autre: il tend les pattes avant et arrières en les écartant (il paraît même que la queue fait « pâles d’hélicoptère » !)
pour offrir le maximum de surface de prise (augmentant par-là S) et minimiser ainsi sa vitesse d’arrivée au sol. Le rapport des
surfaces (S < 8 étages / S > 8 étages pouvant dépasser 2, la vitesse limite de contact peut diminuer d’un facteur 1,5 ce qui augmente les
chances de survie de l’animal et donc fait « redescendre » le pourcentage de décès).

 Allez, un dernier exemple pour ceux (celles) qui préfèrent les maths :
Soit un triangle rectangle comme celui représenté sur la figure à droite. Un
tel triangle est entièrement déterminé, quant à sa forme, par la donnée de
l’un de ses angles (nous considérerons le plus petit soit ), et quant à sa
taille par la données de la valeur de son hypoténuse soit a.
En découpant le triangle original en deux triangles semblables (voir
figure), ces deniers peuvent être définis de la même manière que
précédemment c’est-à-dire par b et pour l’un et par c et pour l’autre.
On peut maintenant exploiter le fait que l’aire d’une figure géométrique
est proportionnelle au produit de deux longueurs (son unité est le mètre-
carré), plus précisément ici au carré de la seule longueur caractéristique
dont nous disposons, c’est-à-dire a).
Ainsi, S = a2*f( ) où f( ) est la constante de proportionnalité sans
dimension donc nécessairement fonction du seul paramètre sans
dimension, l’angle .
Par construction, il est évident que S = S1 + S2 si on appelle S1 et S2 les aires des deux triangles semblables. En appliquant le
même traitement à ces deux aires on obtient S1 = b2*f( ) et S2 = c2*f( ) et l’égalité précédente devient a2*f( ) = b2*f( ) +
c2*f( ). En éliminant la fonction f( ) vous retrouvez un résultat bien connu cher aux profs de math... Cette démonstration
algébrique du théorème de Pythagore possède l’avantage de mettre en évidence les limites dudit théorème et plus
particulièrement sa non-validité dans un espace courbe (lorsqu’on quitte la belle géométrie d’Euclide...). En effet, sur une
sphère par exemple, l’aire d’un triangle rectangle dépend aussi du rayon (elle est alors déterminée par deux longueur
caractéristiques) et notre raisonnement perd sa simplicité et en même temps sa validité.