Montage n° 24 - Nathalie Rion

Montage n° 23
Bilan des puissances dans un dispositif électrique ou électronique ;
détermination expérimentale d'un rendement
Introduction
La puissance, exprimée en Watt, est une grandeur fréquemment utilisée en électricité, qui
caractérise la consommation en électricité, d’appareils de la vie courante : lampe 60 W, four à
micro onde 800 W, etc… La puissance d’un appareil électrique permet d’évaluer la rapidité d’un
transfert d’énergie. Par exemple, plus la puissance d’un four est grande, moins il mettra de
temps pour chauffer un aliment. Au cours de ce montage, intitulé « Bilan des puissances dans
un dispositif électrique ou électronique ; détermination expérimentale d'un rendement », nous
allons dans un premier temps, introduire la notion de puissance, réaliser un bilan de puissance
dans un circuit électrique et enfin, déterminer un rendement. D’une manière générale, que ce
soit en électricité ou en mécanique, on définit un rendement comme étant le rapport de la
puissance disponible (ou utile) sur la puissance consommée. En général, le rendement est
toujours <1 car il y a des pertes diverses que nous allons essayer d’évaluer.
I. Mise en évidence du transfert d’énergie
I.1 Transformation de l’énergie
Livre de 1ère S Hachette
Matériel
- un générateur de tension continue - un moteur (disque de Newton) - une lampe 6V
L’énergie électrique apportée par le générateur est convertie :
- en transfert thermique et rayonnement dans la lampe
- en travail mécanique dans le moteur
Toutes ces énergies sont des énergies utiles. Cependant, une partie
de l’énergie fournie par le générateur est perdue.
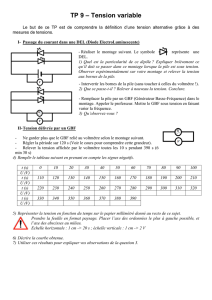
I.2 Etude d’un générateur de tension
I.2.1 Caractéristique tension – intensité
1ère S ou Bellier p.185 (GBF – mais à adapter)
Réaliser le montage en série suivant, mais avec un GBF. On fixe
la fréquence à environ 400 Hz. On fixe l’amplitude du signal et
on fait varier Rh (boîte de résistances). On mesure U aux bornes
du générateur et I (valeurs efficaces)
U (V)
0.9
2.1
2.5
2.8
3.1
3.3
3.5
3.7
3.8
4
4.3
4.4
I (A)
0.097
0.0726
0.0645
0.0579
0.0526
0.048
0.0443
0.041
0.0382
0.0336
0.0284
0.0257
 Tracer UPN = f(I) sur tableur. On obtient une droite U = E - r.I
 Déterminer graphiquement E et r de la pile
U=5,683 – 49,35I. Donc r=49,35  et E=5,683 V (E : fem du géné à
I=0)
faire en prépa la mesure de tous les points sauf un ou deux
autre façon d’obtenir E et r : mesurer E avec un voltmètre aux bornes du GBF (à
vide). Puis, un rhéostat à ses bornes (en dérivation avec un voltmètre), faire varier
Rh pour avoir URh = 0,5*UPN. Mesurer avec un ohmètre Rh = r.
I.2.2 Bilan énergétique
Transition : Définissons un point de fonctionnement particulier (pour
Rh fixé), pour lequel on peut établir un bilan énergétique.
On définit la puissance active comme étant P=UIcosφ. Ici, nous avons un dipôle résistif, donc
P=UI.
 Se placer à un point de fonctionnement (fixer Rh)
 On mesure I=0,0443 A et U = 3,5 V
M
+

 D’où Pfournie au circuit par le GBF = I.U= 0,16 W Pjoule=r.I2= 0,10 W
 Pconsommée par le GBF = I.E= 0,25 W
 Vérifier que Pconsommée par le GBF = Pfournie au circuit par le GBF + Pjoule
 Dans un générateur, une partie de l’énergie est consommée par effet joule car il possède
une résistance interne.
Rendement du générateur : = Pfournie au circuit par le GBF/ Pconsommée par le GBF =0,16/0,25=64 %
II. Etude du transformateur
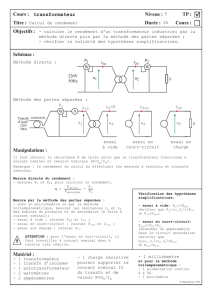
II.1 Description
En utilisant un transfo d’étude.
Un transformateur est constitué de 2 enroulements
enroulés autour d’un circuit magnétique.
L’enroulement primaire est alimenté par une tension
variable. Traversé par un courant, il créé un champ
magnétique variable qui est canalisé dans le circuit
magnétique. Le 2nd enroulement, qui reçoit un flux
magnétique variable, est le siège d’un phénomène
d’induction. On peut mesurer à ses bornes, une fem
d’induction e=-dφ/dt. Le transformateur permet
d’abaisser ou d’élever la tension selon le rapport du
nombre de spires entre secondaire et primaire. Si le
nombre de spires est le même au primaire et au secondaire, le transformateur est utilisé en
transformateur d’isolement.
Le transformateur reçoit de l’énergie au niveau du primaire qui est transmise au secondaire, en
partie seulement, à cause des différentes pertes. On peut recenser 2 types de pertes :
 Les pertes d’énergie par effet joule qui se produisent au niveau des enroulements à
cause de leur résistance interne (échauffement). On appelle ces pertes, les pertes
cuivre.
 Les pertes dans le circuit magnétique qui font que l’intégralité du flux produit au primaire
n’atteint pas toutes les spires du circuit secondaire (hystérésis et courants de Foucault).
On appelle ces pertes, les pertes fer.
II.2 Détermination des pertes fer
essai à vide sous tension primaire nominale
P10 = Pjoule1 + Pjoule2 + Pfer + P20
Dans l’essai à vide, la puissance utile est nulle (P20=I20U20, or I20=0). Donc toute la puissance
délivrée par le primaire est perdue par effet joule dans le primaire (pertes joule au secondaire
=0 car I2=0) et par pertes magnétiques.
Tout transformateur doit porter les indications suivantes sur une plaque ou dans un document
annexe : Tension nominale primaire U1N ici 48 V
Tension nominale secondaire U2N ici 6 V
Puissance apparent nominale SN ici 12 VA
Ceci signifie que le rendement est maximal lorsque l’on se place dans les conditions nominales
(les pertes sont minimisées)
Donc. On mesure P1v=
On peut calculer Pjoule1 en mesurant I1N= et r1= (à l’ohmmètre en
isolant le transfo du système). Pjoule1 = r1I1N2
D’où Pfer = P1v – Pjoule1=Pv1 car les pertes joule sont très faibles.
On peut tracer P1v = f(U1v2) et on montre que les pertes fer (courants de Foucault et hystérésis) sont
proportionnelles à U1v2.
W
ISW800
Alim
variable
V

II.3 Détermination des pertes cuivre
essai en court circuit sous courant secondaire nominal
La mesure du courant secondaire doit être faite à la pince ampèremétrique placée autour d’un
fil court formant le court-circuit car un ampèremètre a une résistance interne et ne constitue pas
un bon court-circuit.
Quand le transformateur est en court-circuit, la puissance utile est nulle (P2cc), la tension
secondaire est nulle (U2cc) mais les courants primaire et secondaire sont importants. Il faut donc
que la tension d’alimentation du transformateur soit très faible : il faut commencer l’essai à 0 V,
puis augmenter peu à peu la tension d’alimentation en surveillant l’intensité du courant
secondaire jusqu’à atteindre le courant nominal secondaire. (Tension nominale secondaire U2N
ici 6 V ; Puissance apparent nominale SN ici 12 VA ; courant nominal secondaire : I2N = SN / U2N
= 2 A)
P1cc = Pjoule1 + Pjoule2 + Pfer + P2cc = Pjoule1 + Pjoule2
Lors de l’essai en court-circuit, comme pour l’essai à vide, toute la puissance utile est
consommée sous forme de pertes. Comme U1cc est très faible et que les pertes fer sont
proportionnelles à U1cc2, elles sont négligeables.
On mesure P1cc = W=Pjoule1 + Pjoule2
II.4 Variation du rendement en fonction de la charge
Quaranta p.496
On fixe U1=U1N et on fait varier
Rch (attention à ne pas
dépasser I2max !!!).
On mesure U2, I2, P1 pour
différentes valeurs de Rch. On
calcule P2=U2I2 et le rendement =P2/P1
Tracer =f(I2)
On note que le rendement passe par un maximal. Vérifier que I2
pour lequel le rendement est maximal est I2N indiqué par le
constructeur sur la plaque signalétique.
II.5 Calcul du rendement en charge pour un courant
secondaire nominal
II.5.1 Charge à utiliser
Nous allons nous placer dans des conditions nominales pour avoir un rendement maximal,
donc U2 6 V et I2  2 A. La charge sera donc constituée d’une résistance Rch d’environ 3 ohms.
On utilise une résistance variable (rhéostat – attention à bien choisir un rhéostat qui supporte la
valeur du courant !!!) dont on règle la valeur à l’ohmmètre avant de mettre la résistance dans le
circuit.
II.5.2 Calcul du rendement
Toujours avec le même montage. Pour calculer le rendement en charge, il faut tenir compte de
toutes les pertes : cuivre puisque les courants sont importants et fer puisque la tension primaire
est nominale.
W
ISW800
Alim
variable
W
ISW800
Alim
variable
V
Rch
P1(W) U2(V) I2(A) P2(W) 
23 12.73 1.33 16.93 0.7361
26 12.63 1.57 19.83 0.7627
33 12.4 2.11 26.16 0.7928
48 11.89 3.26 38.76 0.8075
70 11.18 5.05 56.46 0.8066

 = Puissance utile / puissance fournie = P2 / P1 = U2mes I2mes / P1mes =
A comparer avec th = (P1 – (pcuivre + pfer))/ P1= (P1 – (P1cc + P10))/ P1 =
Les pertes fer sont égales à la puissance mesurée à vide pour la même tension U1V = U1N (c’est
pour pouvoir utiliser ce résultat directement que l’essai à vide a été mené à la tension primaire
nominale).
Les pertes joules ont également été déterminées pour un courant secondaire nominal. Donc on
peut conserver la valeur que l’on a calculé précédemment.
Conclusion
Les essais que nous venons de réaliser sur le transformateur sont réalisés également par les
constructeurs de transformateurs afin de caractériser leurs produits. On arrive maintenant à
fabriquer de très bons transformateurs avec d’excellent rendements (99 %). Il est donc
important, d’un point de vue énergétique, d’évaluer toutes les pertes dans un montage
électronique, électrique, voire même mécanique. Avoir un rendement le plus élevé possible
permet d’utiliser toute la puissance fournie et de faire des économies d’énergie. Pour certaines
application, on est limité, ainsi, le rendement d’un moteur thermique ne pourra pas dépasser le
rendement de Carnot (=1-Tf/Tc), il convient alors, pour avoir un rendement thermodynamique
maximal, d’avoir le plus grand écart possible entre Tf et Tc. On atteint alors des limitations
technologiques : il faut des matériaux qui résistent très bien à la chaleur !!!
BIBLIO
 Bellier p.69 et 178
 Quaranta T4 p.487 (transfo)
Questions
Q1 : quels sont les grands champs d’application des transfo ?
R1 : distribution du courant pour minimiser les pertes par effet joule dans les lignes. On
transporte à très haute tension.
Q2 : quel est le rapport de bobinage dans les transfo EDF ?
R2 : m=U2/U1=40 000 / 230 = 200
Q3 : autres application des transfo ?
R3 : isolement (pour la protection) et adaptation d’impédance
Q4 : comment réduire les pertes fer ?
R4 : les courants de Foucault sont des courants volumiques. On
réduit donc le volume en feuilletant le matériau. Concernant les
pertes par hystérésis, il suffit de choisir un matériau dont l’aire du
cycle est la + petite possible
Q5 : pourquoi mesure-t’on les pertes fer quand le secondaire est
ouvert ?
R5 : P1=P2 + Pfer + Pcuivre. Or, P2=0 et Pcuivre=0 (car i faibles)
Q6 : pourquoi utiliser de gros rhéostats dans ce montage ?
R6 : à cause du courant qui est assez fort. Il faut vérifier la plaque signalétique.
Q7 : comment mesurer la résistance interne d’un générateur ?
R7 : on mesure la tension à vide du générateur. Puis on le met dans un circuit avec un rhéostat
à ses bornes (en dérivation avec un voltmètre), faire varier Rh pour avoir URh = 0,5*UPN.
Mesurer avec un ohmmètre Rh = r.

Q8 : où est dissipée l’énergie dans un circuit ?
R8 : les appareils chauffent (effet joule)
Q9 : quel est l’ordre de grandeur de la résistance interne des appareils utilisés dans les
montages ?
R9 : ampèremètre : r la + petite possible (quand on change de calibre, r change…) ;
 voltmètre : r la + grande possible : presque infinie
 oscillo : 20M ou 40 M
 fils : 0,1
Q10 : énergie dissipée dans une lampe ?
R10 : rayonnement et chauffage (=perte par effet joule). Les lampes basse consommation ont
très peu de pertes par effet joule (ce n’est pas le principe d’un filament qui chauffe).
L’essentiel de l’énergie est utilisée pour le rayonnement
Q11 : consomme t-on moins d’énergie en utilisant un gradateur de lumière ?
R11 : non !!! l’énergie qui n’est pas utilisée pour le rayonnement est dissipée par effet joule.
Donc moins la lampe éclaire, + on chauffe !!!